
Big O in probability notation
Encyclopedia
The order in probability notation is used in probability theory
and statistical theory
in direct parallel to the big-O notation which is standard in mathematics
. Where the big-O notation deals with the convergence of sequences or sets of ordinary numbers, the order in probability notation deals with convergence of sets of random variables
, where convergence is in the sense of convergence in probability.
For a set of random variables Xn and a corresponding set of constants an (both indexed by n which need not be discrete), the notation
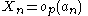
means that the set of values Xn/an converges to zero in probability as n approaches an appropriate limit.
Equivalently, Xn = op(an) can be written as an op(1) where Xn = op(1) is defined as,
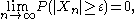
for every positive ε.
The notation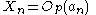
means that the set of values Xn/an is bounded in the limit in probability.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistical theory
Statistical theory
The theory of statistics provides a basis for the whole range of techniques, in both study design and data analysis, that are used within applications of statistics. The theory covers approaches to statistical-decision problems and to statistical inference, and the actions and deductions that...
in direct parallel to the big-O notation which is standard in mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
. Where the big-O notation deals with the convergence of sequences or sets of ordinary numbers, the order in probability notation deals with convergence of sets of random variables
Convergence of random variables
In probability theory, there exist several different notions of convergence of random variables. The convergence of sequences of random variables to some limit random variable is an important concept in probability theory, and its applications to statistics and stochastic processes...
, where convergence is in the sense of convergence in probability.
For a set of random variables Xn and a corresponding set of constants an (both indexed by n which need not be discrete), the notation
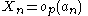
means that the set of values Xn/an converges to zero in probability as n approaches an appropriate limit.
Equivalently, Xn = op(an) can be written as an op(1) where Xn = op(1) is defined as,
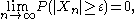
for every positive ε.
The notation
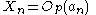
means that the set of values Xn/an is bounded in the limit in probability.

