
Linear response function
Encyclopedia
A linear response function describes the input-output relationship of a signal transducer such as a radio turning electromagnetic waves into music or a neuron turning synaptic input into a response. Because of its many applications in information theory, physics and engineering there exist alternative names for specific linear response functions
such as susceptibility
, impulse response
or impedance
, see also transfer function
. The concept of a Green's function
or fundamental solution
of an ordinary differential equation is closely related.
 , and the response of the system by
, and the response of the system by 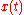 . Generally, the value of
. Generally, the value of 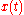 will depend not only on the present value of
will depend not only on the present value of 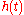 , but also on past values. Approximately
, but also on past values. Approximately 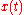 is a weighted sum of the previous values of
is a weighted sum of the previous values of  , with the weights given by the linear response function
, with the weights given by the linear response function 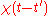 :
:
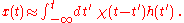
This expression is the leading order term of a Volterra-expansion
. If the system in question is highly non-linear, higher order terms become important and the signal transducer can not adequately be described just by its linear response function.
The Fourier transform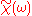 of the linear response function is very useful as it
of the linear response function is very useful as it
describes the output of the system if the input is a sine wave with frequency
with frequency  . The output reads
. The output reads

with amplitude gain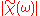 and phase shift
and phase shift 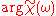 .
.
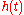
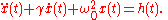
The Fourier transform
of the linear response function is given as
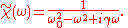
From this representation, we see that the Fourier transform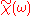 of the linear response function attains a maximum for
of the linear response function attains a maximum for  : The damped harmonic oscillator acts as a band pass filter.
: The damped harmonic oscillator acts as a band pass filter.
such as susceptibility
Susceptibility
*In physics, the susceptibility of a material or substance describes its response to an applied field. There are many kinds of susceptibilities, for example:These two susceptibilities are particular examples of a linear response function;...
, impulse response
Impulse response
In signal processing, the impulse response, or impulse response function , of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response refers to the reaction of any dynamic system in response to some external change...
or impedance
Electrical impedance
Electrical impedance, or simply impedance, is the measure of the opposition that an electrical circuit presents to the passage of a current when a voltage is applied. In quantitative terms, it is the complex ratio of the voltage to the current in an alternating current circuit...
, see also transfer function
Transfer function
A transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...
. The concept of a Green's function
Green's function
In mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
or fundamental solution
Fundamental solution
In mathematics, a fundamental solution for a linear partial differential operator L is a formulation in the language of distribution theory of the older idea of a Green's function...
of an ordinary differential equation is closely related.
Mathematical definition
Denote the input of a system by , and the response of the system by
, and the response of the system by 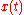 . Generally, the value of
. Generally, the value of 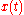 will depend not only on the present value of
will depend not only on the present value of 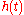 , but also on past values. Approximately
, but also on past values. Approximately 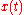 is a weighted sum of the previous values of
is a weighted sum of the previous values of  , with the weights given by the linear response function
, with the weights given by the linear response function 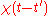 :
: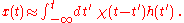
This expression is the leading order term of a Volterra-expansion
Volterra Series
The Volterra series is a model for non-linear behavior similar to the Taylor series. It differs from the Taylor series in its ability to capture 'memory' effects. The Taylor series can be used to approximate the response of a nonlinear system to a given input if the output of this system depends...
. If the system in question is highly non-linear, higher order terms become important and the signal transducer can not adequately be described just by its linear response function.
The Fourier transform
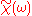 of the linear response function is very useful as it
of the linear response function is very useful as itdescribes the output of the system if the input is a sine wave
 with frequency
with frequency  . The output reads
. The output reads
with amplitude gain
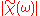 and phase shift
and phase shift 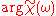 .
.Example
Consider the damped harmonic oscillator, which gets an external driving by the input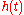
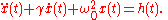
The Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of the linear response function is given as

From this representation, we see that the Fourier transform
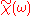 of the linear response function attains a maximum for
of the linear response function attains a maximum for  : The damped harmonic oscillator acts as a band pass filter.
: The damped harmonic oscillator acts as a band pass filter.See also
- ConvolutionConvolutionIn mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
- Green–Kubo relations
- Fluctuation theoremFluctuation theoremThe fluctuation theorem , which originated from statistical mechanics, deals with the relative probability that the entropy of a system which is currently away from thermodynamic equilibrium will increase or decrease over a given amount of time...
- Dispersion (optics)Dispersion (optics)In optics, dispersion is the phenomenon in which the phase velocity of a wave depends on its frequency, or alternatively when the group velocity depends on the frequency.Media having such a property are termed dispersive media...
- Lindblad equationLindblad equationIn quantum mechanics, the Kossakowski–Lindblad equation or master equation in the Lindblad form is the most general type of markovian and time-homogeneous master equation describing non-unitary evolution of the density matrix \rho that is trace preserving and completely positive for any initial...
- Semilinear responseSemilinear Response-Applications:The original motivation for introducing SLRT was the study of mesosopic conductance.The term SLRT has been coined inwhere it has been applied to the calculation of energy absorption by metallic grains....

