
Semilinear Response
Encyclopedia
Applications
The original motivation for introducing SLRT was the study of mesosopic conductance.
The term SLRT has been coined in
where it has been applied to the calculation of energy absorption by metallic grains.
Later the theory has been applied for analysing the rate of heating of atoms in vibrating traps
.
Definition of semilinear response
Consider a system that is driven by a source that has
that hasa power spectrum
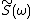 . The latter is defined
. The latter is definedas the Fourier transform of
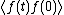 .
.In linear response theory (LRT) the driving source induces a steady state
which is only slightly different from the equilibrium state.
In such circumstances the response (
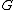 ) is a linear functional of the power spectrum:
) is a linear functional of the power spectrum:-
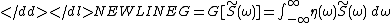
In the traditional LRT context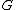 represents the rate of heating,
represents the rate of heating,
and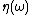 can be defined as the absorption coefficient.
can be defined as the absorption coefficient.
Whenever such relation applies
-

-
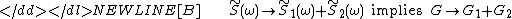
If the driving is very strong the response becomes non-linear, meaning that both properties [A] and [B] do not hold. But there is a class of systems whose response becomes semi-linear, i.e. the first property [A] still holds, but not [B].
Resistor network modeling
SLRT applies whenever the driving is strong enough such that relaxation to the steady state is slow compared with the driven dynamics. Yet one assumes that the system can be modeled as a resistor network, mathematically expressed as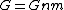 .
.
The notation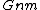 stands for the usual electrical engineering calculation of a two terminal conductance of a given resistor network. For example parallel connections imply
stands for the usual electrical engineering calculation of a two terminal conductance of a given resistor network. For example parallel connections imply 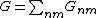 , while serial connections imply
, while serial connections imply 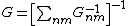 . Resistor network calculation is manifestly semi-linear because it satisfies
. Resistor network calculation is manifestly semi-linear because it satisfies  , but in general
, but in general 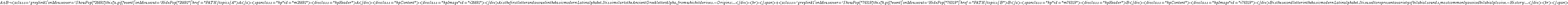 .
.
Fermi golden rule picture
In the quantum mechanical calculation of energy absorption, the represent Fermi-golden-rule transition rates between energy levels. If only neighboring levels are coupled, serial addition implies
represent Fermi-golden-rule transition rates between energy levels. If only neighboring levels are coupled, serial addition implies
-
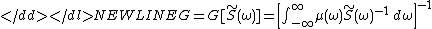
which is manifestly semi-linear. Results for sparse networks, that are encountered in the analysis of weakly chaotic driven systems,
are more interesting and can be obtained using a generalized variable range hopping (VRH) scheme.
-
-
-

