Laughlin wavefunction
Encyclopedia
In condensed matter physics
, the Laughlin wavefunction is an ansatz
, proposed by Robert Laughlin
for the ground state
of a two-dimensional electron gas placed in a uniform background magnetic field
in the presence of a uniform jellium
background when the filling factor
of the lowest Landau level is 1/n where n is an odd positive integer. It was constructed to explain the observation of one third of an electron charge in the Fractional quantum Hall effect
, and Laughlin received one third of the Nobel Prize in Physics
in 1998 for his discovery. Being an ansatz, it's not exact, but qualitatively, it reproduces many features of the exact solution and quantitatively, it is pretty good.
If we ignore the jellium and mutual Coulomb repulsion between the electrons as a zeroth order approximation, we have an infinitely degenerate lowest Landau level and with a filling factor of 1/n, we'd expect that all of the electrons would lie in the LLL. Turning on the interactions, we can make the approximation that all of the electrons lie in the LLL. If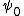
is the single particle wavefunction of the LLL state with the lowest orbital angular momentum, then the Laughlin ansatz for the multiparticle wavefunction is
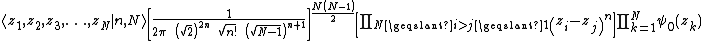
where
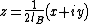
and
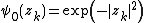
and (Gaussian units
)
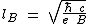
and
and 
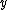are coordinates in the xy plane. Here 
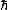is Planck's constant, 
is the electron charge,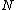 
is the total umber of particles, and 
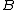is the magnetic field
, which is perpendicular to the xy plane. The subscripts on z identify the particle. In order for the wavefunction to describe fermion
s, n must be an odd integer. This forces the wavefunction to be antisymmetric under particle interchange. The angular momentum for this state is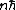
.
s. The expectation value of the interaction energy for a pair of quasiparticles is
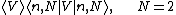
where the screened potential is (see Coulomb potential between two current loops embedded in a magnetic field)
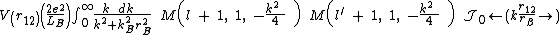
where
is a confluent hypergeometric function
and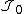
is a Bessel function
of the first kind. Here,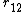
is the distance between the centers of two current loops, 
is the magnitude of the electron charge,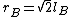 
is the quantum version of the Larmor radius, and 
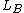is the thickness of the electron gas in the direction of the magnetic field. The angular momenta
of the two individual current loops are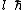
and 
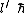where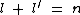 
. The inverse screening length is given by (Gaussian units
)
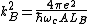
where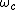
is the cyclotron frequency, and 
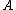is the area of the electron gas in the xy plane.
The interaction energy evaluates to:
|
|}
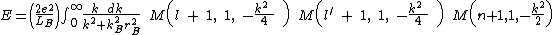
To obtain this result we have made the change of integration variables
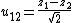
and
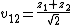
and noted (see Common integrals in quantum field theory)
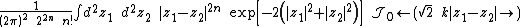
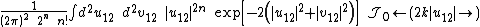
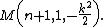
The interaction energy has minima for (Figure 1)
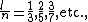
and
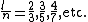
For these values of the ratio of angular momenta, the energy is plotted in Figure 2 as a function of
.
Condensed matter physics
Condensed matter physics deals with the physical properties of condensed phases of matter. These properties appear when a number of atoms at the supramolecular and macromolecular scale interact strongly and adhere to each other or are otherwise highly concentrated in a system. The most familiar...
, the Laughlin wavefunction is an ansatz
Ansatz
Ansatz is a German noun with several meanings in the English language.It is widely encountered in physics and mathematics literature.Since ansatz is a noun, in German texts the initial a of this word is always capitalised.-Definition:...
, proposed by Robert Laughlin
Robert B. Laughlin
Robert Betts Laughlin is a professor of Physics and Applied Physics at Stanford University. Along with Horst L. Störmer of Columbia University and Daniel C. Tsui of Princeton University, he was awarded a share of the 1998 Nobel Prize in physics for their explanation of the fractional quantum Hall...
for the ground state
Ground state
The ground state of a quantum mechanical system is its lowest-energy state; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state...
of a two-dimensional electron gas placed in a uniform background magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
in the presence of a uniform jellium
Jellium
Jellium, also known as the uniform electron gas or homogeneous electron gas , is a quantum mechanical model of interacting electrons in a solid where the positive charges are assumed to be uniformly distributed in space whence the electron densityis a uniform quantity as well in space...
background when the filling factor
Filling factor
Filling factor, ~F~, is a quantity measuring the efficiency of absorption of pump in the core of a double-clad fiber.-Definition:The efficiency of absorption of pumping energy in the fiber is an important parameter of a double-clad fiber laser...
of the lowest Landau level is 1/n where n is an odd positive integer. It was constructed to explain the observation of one third of an electron charge in the Fractional quantum Hall effect
Fractional quantum Hall effect
The fractional quantum Hall effect is a physical phenomenon in which the Hall conductance of 2D electrons shows precisely quantised plateaus at fractional values of e^2/h. It is a property of a collective state in which electrons bind magnetic flux lines to make new quasiparticles, and excitations...
, and Laughlin received one third of the Nobel Prize in Physics
Nobel Prize in Physics
The Nobel Prize in Physics is awarded once a year by the Royal Swedish Academy of Sciences. It is one of the five Nobel Prizes established by the will of Alfred Nobel in 1895 and awarded since 1901; the others are the Nobel Prize in Chemistry, Nobel Prize in Literature, Nobel Peace Prize, and...
in 1998 for his discovery. Being an ansatz, it's not exact, but qualitatively, it reproduces many features of the exact solution and quantitatively, it is pretty good.
If we ignore the jellium and mutual Coulomb repulsion between the electrons as a zeroth order approximation, we have an infinitely degenerate lowest Landau level and with a filling factor of 1/n, we'd expect that all of the electrons would lie in the LLL. Turning on the interactions, we can make the approximation that all of the electrons lie in the LLL. If
is the single particle wavefunction of the LLL state with the lowest orbital angular momentum, then the Laughlin ansatz for the multiparticle wavefunction is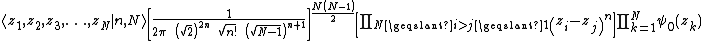where
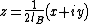
and
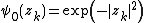
and (Gaussian units
Gaussian units
Gaussian units comprise a metric system of physical units. This system is the most common of the several electromagnetic unit systems based on cgs units. It is also called the Gaussian unit system, Gaussian-cgs units, or often just cgs units...
)
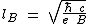
and
and 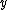are coordinates in the xy plane. Here 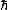is Planck's constant, is the electron charge, 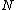is the total umber of particles, and 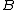is the magnetic fieldMagnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
, which is perpendicular to the xy plane. The subscripts on z identify the particle. In order for the wavefunction to describe fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s, n must be an odd integer. This forces the wavefunction to be antisymmetric under particle interchange. The angular momentum for this state is
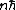.Energy of interaction for two particles
The Laughlin wavefunction is the multiparticle wavefunction for quasiparticleQuasiparticle
In physics, quasiparticles are emergent phenomena that occur when a microscopically complicated system such as a solid behaves as if it contained different weakly interacting particles in free space...
s. The expectation value of the interaction energy for a pair of quasiparticles is
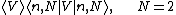
where the screened potential is (see Coulomb potential between two current loops embedded in a magnetic field)
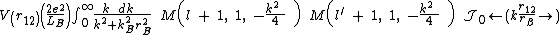
where
is a confluent hypergeometric functionConfluent hypergeometric function
In mathematics, a confluent hypergeometric function is a solution of a confluent hypergeometric equation, which is a degenerate form of a hypergeometric differential equation where two of the three regular singularities merge into an irregular singularity...
and
is a Bessel functionBessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
of the first kind. Here,
is the distance between the centers of two current loops, is the magnitude of the electron charge, 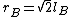is the quantum version of the Larmor radius, and 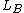is the thickness of the electron gas in the direction of the magnetic field. The angular momentaAngular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
of the two individual current loops are
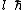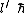and where 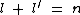. The inverse screening length is given by (Gaussian unitsGaussian units
Gaussian units comprise a metric system of physical units. This system is the most common of the several electromagnetic unit systems based on cgs units. It is also called the Gaussian unit system, Gaussian-cgs units, or often just cgs units...
)
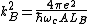
where
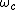is the cyclotron frequency, and 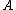is the area of the electron gas in the xy plane.The interaction energy evaluates to:
-
- {|cellpadding="2" style="border:2px solid #ccccff"
|
|}
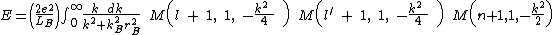
To obtain this result we have made the change of integration variables
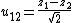
and
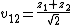
and noted (see Common integrals in quantum field theory)
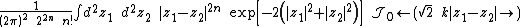
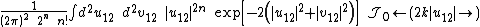
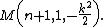
The interaction energy has minima for (Figure 1)
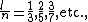
and
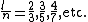
For these values of the ratio of angular momenta, the energy is plotted in Figure 2 as a function of
.See also
- Landau level
- Fractional quantum Hall effectFractional quantum Hall effectThe fractional quantum Hall effect is a physical phenomenon in which the Hall conductance of 2D electrons shows precisely quantised plateaus at fractional values of e^2/h. It is a property of a collective state in which electrons bind magnetic flux lines to make new quasiparticles, and excitations...
- Coulomb potential between two current loops embedded in a magnetic field