Large eddy simulation
Encyclopedia
Large eddy simulation is a mathematical model for turbulence
used in computational fluid dynamics
. It was initially proposed in 1963 by Joseph Smagorinsky
to simulate atmospheric air currents, and many of the issues unique to LES were first explored by Deardorff (1970). LES grew rapidly and is currently applied in a wide variety of engineering applications, including combustion, acoustics, and simulations of the atmospheric boundary layer. LES operates on the Navier-Stokes equations
to reduce the range of length scales of the solution, reducing the computational cost.
The principal operation in large eddy simulation is low-pass filtering
. This operation is applied to the Navier-Stokes equations to eliminate small scales of the solution. This reduces the computational cost of the simulation. The governing equations are thus transformed, and the solution is a filtered velocity field. Which of the "small" length and time scales to eliminate are selected according to turbulence theory and available computational resources.
Large eddy simulation resolves large scales of the flow field solution allowing better fidelity than alternative approaches such as Reynolds-averaged Navier-Stokes
(RANS) methods. It also models the smallest (and most expensive) scales of the solution, rather than resolving them as direct numerical simulation
(DNS) does. This makes the computational cost for practical engineering systems with complex geometry or flow configurations, such as turbulent jets, pumps, vehicles, and landing gear, attainable using supercomputer
s. In contrast, direct numerical simulation
, which resolves every scale of the solution, is prohibitively expensive for nearly all systems with complex geometry or flow configurations.
can be applied to a spatial and temporal field
and perform a spatial filtering operation, a temporal filtering operation, or both. The filtered field, denoted with a bar, is defined as:
where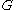
is the filter convolution kernel. This can also be written as:
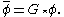
The filter kernel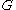
has an associated cutoff length scale 
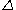and cutoff time scale 
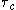. Scales smaller than these are eliminated from 
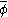. Using the above filter definition, any field 
may be split up into a filtered and sub-filtered (denoted with a prime) portion, as
It is important to note that the large eddy simulation filtering operation
does not satisfy the properties of a Reynolds operator
.
. There are differences between the incompressible and compressible LES governing equations, which lead to the definition of a new filtering operation.
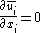
and the filtered Navier-Stokes equations,
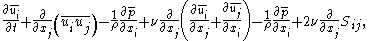
where
is the filtered pressure field and 
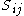is the rate-of-strain tensor. The nonlinear filtered advection term 
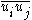is the chief cause of difficulty in LES modeling. It requires knowledge of the unfiltered velocity field, which is unknown, so it must be modeled. The analysis that follows illustrates the difficulty caused by the nonlinearity, namely, that it causes interaction between large and small scales, preventing separation of scales.
The filtered advection term can be split up, following Leonard (1974), as:
where
is the residual stress tensor, so that the filtered Navier Stokes equations become
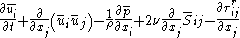
with the residual stress tensor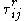
grouping all unclosed terms. Leonard decomposed this stress tensor as 
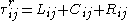and provided physical interpretations for each term. 
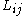, the Leonard tensor, represents interactions among large scales, 
, the Reynolds stress-like term, represents interactions among the sub-filter scales (SFS), and 
, the Clark tensor, represents cross-scale interactions between large and small scales. Modeling the unclosed term 
is the task of SFS models (also referred to as sub-grid scale, or SGS, models). This is made challenging by the fact that the sub-filter scale stress tensor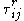 
must account for interactions among all scales, including filtered scales with unfiltered scales.
The filtered governing equation for a passive scalar
, such as mixture fraction or temperature, can be written as
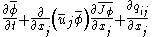
where
is the diffusive flux of 
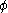, and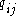 
is the sub-filter stress tensor for the scalar 
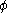. The filtered diffusive flux 
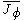is unclosed, unless a particular form is assumed for it (e.g. a gradient diffusion model 
). 
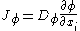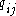is defined analogously to 
,
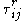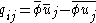
and can similarly be split up into contributions from interactions between various scales. This sub-filter tensor also requires a sub-filter model.
which results in an additional sub-filter term. However, it is desirable to avoid having to model the sub-filter scales of the mass conservation equation. For this reason, Favre proposed a density-weighted filtering operation, called Favre filtering, defined for an arbitrary quantity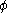
as:
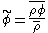
which, in the limit of incompressibility, becomes the normal filtering operation. This makes the conservation of mass equation:
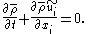
This concept can then be extended to write the Favre-filtered momentum equation for compressible flow. Following Vreman:
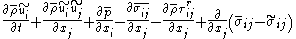
where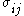
is the shear stress tensor, given for a Newtonian fluid by:
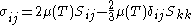
and the term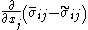
represents a sub-filter viscous contribution from evaluating the viscosity 
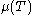using the Favre-filtered temperature 
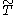. The subgrid stress tensor for the Favre-filtered momentum field is given by
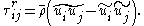
By analogy, the Leonard decomposition may also be written for the residual stress tensor for a filtered triple product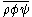
. The triple product can be rewritten using the Favre filtering operator as 
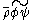, which is an unclosed term (it requires knowledge of the fields 
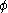and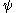 
, when only the fields 
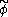and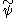 
are known). It can be broken up in a manner analogous to 
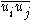above, which results in a sub-filter stress tensor 
. This sub-filter term can be split up into contributions from three types of interactions: the Leondard tensor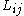 
, representing interactions among resolved scales; the Clark tensor 
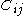, representing interactions between resolved and unresolved scales; and the Reynolds tensor 
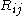, which represents interactions among unresolved scales.
and the total filtered kinetic energy can be decomposed into two terms: the kinetic energy of the filtered velocity field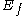
,
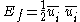
and the residual kinetic energy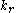
,
such that
.
The conservation equation for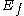
can be obtained by multiplying the filtered momentum transport equation by 
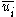to yield:
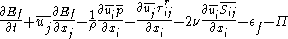
where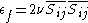
is the dissipation of kinetic energy of the filtered velocity field by viscous stress, and 
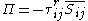represents the sub-filter scale (SFS) dissipation of kinetic energy.
The terms on the left-hand side represent transport, and the terms on the right-hand side are sink terms that dissipate kinetic energy.
The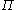
SFS dissipation term is of particular interest, since it represents the transfer of energy from large resolved scales to small unresolved scales. On average, 
transfers energy from large to small scales. However, instantaneously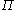 
can be positive or negative, meaning it can also act as a source term for 
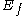, the kinetic energy of the filtered velocity field. The transfer of energy from unresolved to resolved scales is called backscatter (and likewise the transfer of energy from resolved to unresolved scales is called forward-scatter).
. LES resolves scales from the domain size
down to the filter size 
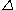, and as such a substantial portion of high wave number turbulent fluctuations must be resolved. This requires either high-order numerical schemes, or fine grid resolution if low-order numerical schemes are used. Chapter 13 of Pope addresses the question of how fine a grid resolution 
is needed to resolve a filtered velocity field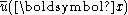 
. Ghosal found that for low-order discretization schemes, such as those used in finite volume methods, the truncation error can be the same order as the subfilter scale contributions, unless the filter width 
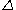is considerably larger than the grid spacing 
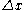. While even-order schemes have truncation error, they are non-dissipative, and because subfilter scale models are dissipative, even-order schemes will not affect the subfilter scale model contributions as strongly as dissipative schemes.
In explicit filtering, an LES filter
is applied to the discretized Navier-Stokes equations, providing a well-defined filter shape and reducing the truncation error. However, explicit filtering requires a finer grid than implicit filtering, and the computational cost increases with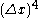
. Chapter 8 of Sagaut (2006) covers LES numerics in greater detail.
The resolved sub-filter scales represent the scales with wave numbers larger than the cutoff wave number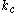
, but whose effects are dampened by the filter. Resolved sub-filter scales only exist when filters non-local in wave-space are used (such as a box or Gaussian filter). These resolved sub-filter scales must be modeled using filter reconstruction.
Sub-grid scales are any scales that are smaller than the cutoff filter width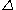
. The form of the SGS model depends on the filter implementation. As mentioned in the Numerical methods for LES section, if the filter is implicit, there is no SGS model implemented. Only explicit filters require SGS models.
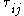is modeled as:
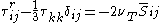
where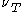
is the turbulent eddy viscosity and 
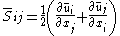is the rate-of-strain tensor.
Based on dimensional analysis, the eddy viscosity must have units of
. Most eddy viscosity SGS models model the eddy viscosity as the product of a characteristic length scale and a characteristic velocity scale.
and used in the first LES simulation by Deardorff. It models the eddy viscosity as:
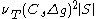
where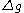
is the grid size and 
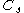is a constant.
This method assumes that the energy production and dissipation of the small scales are in equilibrium - that is,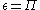
.
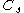for different flow configurations. In an attempt to formulate a more universal approach to SGS models, Germano et al. proposed a dynamic Smagorinsky model, which utilized two filters: a grid LES filter, denoted 
, and a test LES filter, denoted 
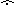. In this case, the resolved turbulent stress tensor 
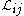is defined as
which is also called the Germano identity. The quantity
is the residual stress tensor for the test filter, and 
is the residual stress tensor for the grid filter.
represents the contribution to the SGS stresses by length scales smaller than the test filter width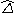 
but larger than the grid filter width 
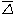. This allows the value of the Smagorinsky model to adapt to the instantaneous state of the flow.
The dynamic SGS model yields an equation for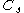
:
where
and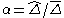 
. However, this procedure was numerically unstable, and additionally finding the value of 
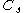was complicated by the fact that it was an overdetermined problem (one equation with five unknowns).
Because of these issues, Germano enforced the dynamic constant in an average sense, so that the equation for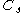
was actually:
Lilly proposed a modification to the dynamic model that utilized a least squares method to find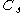
, making the former version more stable and making the method more applicable.
, the Navier-Stokes equations for an incompressible fluid are
Turbulence
In fluid dynamics, turbulence or turbulent flow is a flow regime characterized by chaotic and stochastic property changes. This includes low momentum diffusion, high momentum convection, and rapid variation of pressure and velocity in space and time...
used in computational fluid dynamics
Computational fluid dynamics
Computational fluid dynamics, usually abbreviated as CFD, is a branch of fluid mechanics that uses numerical methods and algorithms to solve and analyze problems that involve fluid flows. Computers are used to perform the calculations required to simulate the interaction of liquids and gases with...
. It was initially proposed in 1963 by Joseph Smagorinsky
Joseph Smagorinsky
Joseph Smagorinsky was an American meteorologist and the first director of the National Oceanic and Atmospheric Administration's Geophysical Fluid Dynamics Laboratory.- Early life :...
to simulate atmospheric air currents, and many of the issues unique to LES were first explored by Deardorff (1970). LES grew rapidly and is currently applied in a wide variety of engineering applications, including combustion, acoustics, and simulations of the atmospheric boundary layer. LES operates on the Navier-Stokes equations
Navier-Stokes equations
In physics, the Navier–Stokes equations, named after Claude-Louis Navier and George Gabriel Stokes, describe the motion of fluid substances. These equations arise from applying Newton's second law to fluid motion, together with the assumption that the fluid stress is the sum of a diffusing viscous...
to reduce the range of length scales of the solution, reducing the computational cost.
The principal operation in large eddy simulation is low-pass filtering
Filter (signal processing)
In signal processing, a filter is a device or process that removes from a signal some unwanted component or feature. Filtering is a class of signal processing, the defining feature of filters being the complete or partial suppression of some aspect of the signal...
. This operation is applied to the Navier-Stokes equations to eliminate small scales of the solution. This reduces the computational cost of the simulation. The governing equations are thus transformed, and the solution is a filtered velocity field. Which of the "small" length and time scales to eliminate are selected according to turbulence theory and available computational resources.
Large eddy simulation resolves large scales of the flow field solution allowing better fidelity than alternative approaches such as Reynolds-averaged Navier-Stokes
Reynolds-averaged Navier-Stokes equations
The Reynolds-averaged Navier–Stokes equations are time-averagedequations of motion for fluid flow. The idea behind the equations is Reynolds decomposition, whereby an instantaneous quantity is decomposed into its time-averaged and fluctuating quantities, an idea first proposed by Osborne Reynolds...
(RANS) methods. It also models the smallest (and most expensive) scales of the solution, rather than resolving them as direct numerical simulation
Direct numerical simulation
A direct numerical simulation is a simulation in computational fluid dynamics in which the Navier-Stokes equations are numerically solved without any turbulence model...
(DNS) does. This makes the computational cost for practical engineering systems with complex geometry or flow configurations, such as turbulent jets, pumps, vehicles, and landing gear, attainable using supercomputer
Supercomputer
A supercomputer is a computer at the frontline of current processing capacity, particularly speed of calculation.Supercomputers are used for highly calculation-intensive tasks such as problems including quantum physics, weather forecasting, climate research, molecular modeling A supercomputer is a...
s. In contrast, direct numerical simulation
Direct numerical simulation
A direct numerical simulation is a simulation in computational fluid dynamics in which the Navier-Stokes equations are numerically solved without any turbulence model...
, which resolves every scale of the solution, is prohibitively expensive for nearly all systems with complex geometry or flow configurations.
Filter Definition and Properties
An LES filterFilter (large eddy simulation)
Filtering in the context of large eddy simulation is a mathematical operation intended to remove a range of small scales from the solution to the Navier-Stokes equations...
can be applied to a spatial and temporal field
and perform a spatial filtering operation, a temporal filtering operation, or both. The filtered field, denoted with a bar, is defined as:where
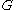is the filter convolution kernel. This can also be written as: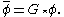The filter kernel
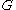has an associated cutoff length scale 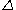and cutoff time scale 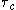. Scales smaller than these are eliminated from 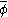. Using the above filter definition, any field may be split up into a filtered and sub-filtered (denoted with a prime) portion, asIt is important to note that the large eddy simulation filtering operation
Filter (large eddy simulation)
Filtering in the context of large eddy simulation is a mathematical operation intended to remove a range of small scales from the solution to the Navier-Stokes equations...
does not satisfy the properties of a Reynolds operator
Reynolds operator
In fluid dynamics and invariant theory, a Reynolds operator is a mathematical operator given by averaging something over a group action, that satisfies a set of properties called Reynolds rules...
.
Filtered governing equations
The governing equations of LES are obtained by filtering the partial differential equations governing the flow field. There are differences between the incompressible and compressible LES governing equations, which lead to the definition of a new filtering operation.Incompressible flow
For incompressible flow, the continuity equation and Navier-Stokes equations are filtered, yielding the filtered incompressible continuity equation,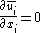and the filtered Navier-Stokes equations,
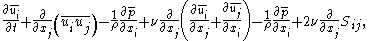
where
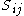is the filtered pressure field and is the rate-of-strain tensor. The nonlinear filtered advection term 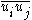is the chief cause of difficulty in LES modeling. It requires knowledge of the unfiltered velocity field, which is unknown, so it must be modeled. The analysis that follows illustrates the difficulty caused by the nonlinearity, namely, that it causes interaction between large and small scales, preventing separation of scales.The filtered advection term can be split up, following Leonard (1974), as:
where
is the residual stress tensor, so that the filtered Navier Stokes equations become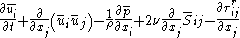with the residual stress tensor
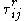grouping all unclosed terms. Leonard decomposed this stress tensor as 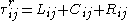and provided physical interpretations for each term. 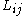, the Leonard tensor, represents interactions among large scales, , the Reynolds stress-like term, represents interactions among the sub-filter scales (SFS), and , the Clark tensor, represents cross-scale interactions between large and small scales. Modeling the unclosed term is the task of SFS models (also referred to as sub-grid scale, or SGS, models). This is made challenging by the fact that the sub-filter scale stress tensor 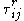must account for interactions among all scales, including filtered scales with unfiltered scales.The filtered governing equation for a passive scalar
, such as mixture fraction or temperature, can be written as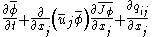where
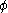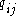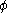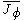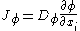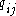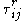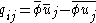
is the diffusive flux of , and is the sub-filter stress tensor for the scalar . The filtered diffusive flux is unclosed, unless a particular form is assumed for it (e.g. a gradient diffusion model ). is defined analogously to ,and can similarly be split up into contributions from interactions between various scales. This sub-filter tensor also requires a sub-filter model.
Compressible governing equations
For the governing equations of compressible flow, each equation, starting with the conservation of mass, is filtered. This gives:which results in an additional sub-filter term. However, it is desirable to avoid having to model the sub-filter scales of the mass conservation equation. For this reason, Favre proposed a density-weighted filtering operation, called Favre filtering, defined for an arbitrary quantity
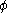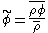
as:which, in the limit of incompressibility, becomes the normal filtering operation. This makes the conservation of mass equation:
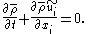
This concept can then be extended to write the Favre-filtered momentum equation for compressible flow. Following Vreman:
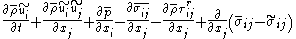
where
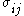is the shear stress tensor, given for a Newtonian fluid by: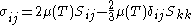and the term
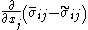represents a sub-filter viscous contribution from evaluating the viscosity 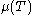using the Favre-filtered temperature 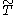. The subgrid stress tensor for the Favre-filtered momentum field is given by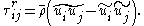By analogy, the Leonard decomposition may also be written for the residual stress tensor for a filtered triple product
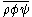. The triple product can be rewritten using the Favre filtering operator as 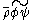, which is an unclosed term (it requires knowledge of the fields 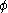and 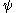, when only the fields 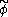and 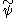are known). It can be broken up in a manner analogous to 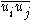above, which results in a sub-filter stress tensor . This sub-filter term can be split up into contributions from three types of interactions: the Leondard tensor 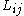, representing interactions among resolved scales; the Clark tensor 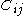, representing interactions between resolved and unresolved scales; and the Reynolds tensor 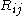, which represents interactions among unresolved scales.Filtered kinetic energy equation
In addition to the filtered mass and momentum equations, filtering the kinetic energy equation can provide additional insight. The kinetic energy field can be filtered to yield the total filtered kinetic energy:and the total filtered kinetic energy can be decomposed into two terms: the kinetic energy of the filtered velocity field
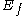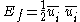
,and the residual kinetic energy
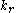,such that
.The conservation equation for
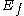can be obtained by multiplying the filtered momentum transport equation by 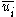to yield: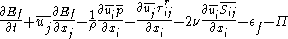where
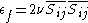is the dissipation of kinetic energy of the filtered velocity field by viscous stress, and 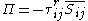represents the sub-filter scale (SFS) dissipation of kinetic energy.The terms on the left-hand side represent transport, and the terms on the right-hand side are sink terms that dissipate kinetic energy.
The
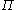SFS dissipation term is of particular interest, since it represents the transfer of energy from large resolved scales to small unresolved scales. On average, transfers energy from large to small scales. However, instantaneously 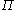can be positive or negative, meaning it can also act as a source term for 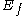, the kinetic energy of the filtered velocity field. The transfer of energy from unresolved to resolved scales is called backscatter (and likewise the transfer of energy from resolved to unresolved scales is called forward-scatter).Numerical Methods for LES
Large eddy simulation involves the solution to the discrete filtered governing equations using computational fluid dynamicsComputational fluid dynamics
Computational fluid dynamics, usually abbreviated as CFD, is a branch of fluid mechanics that uses numerical methods and algorithms to solve and analyze problems that involve fluid flows. Computers are used to perform the calculations required to simulate the interaction of liquids and gases with...
. LES resolves scales from the domain size
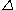down to the filter size , and as such a substantial portion of high wave number turbulent fluctuations must be resolved. This requires either high-order numerical schemes, or fine grid resolution if low-order numerical schemes are used. Chapter 13 of Pope addresses the question of how fine a grid resolution is needed to resolve a filtered velocity field 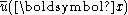. Ghosal found that for low-order discretization schemes, such as those used in finite volume methods, the truncation error can be the same order as the subfilter scale contributions, unless the filter width 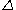is considerably larger than the grid spacing 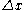. While even-order schemes have truncation error, they are non-dissipative, and because subfilter scale models are dissipative, even-order schemes will not affect the subfilter scale model contributions as strongly as dissipative schemes.Filter implementation
The filtering operation in large eddy simulation can be implicit or explicit. Implicit filtering recognizes that the subfilter scale model will dissipate in the same manner as many numerical schemes. In this way, the grid, or the numerical discretization scheme, can be assumed to be the LES low-pass filter. While this takes full advantage of the grid resolution, and eliminates the computational cost of calculating a subfilter scale model term, it is difficult to determine the shape of the LES filter that is associated with some numerical issues. Additionally, truncation error can also become an issue.In explicit filtering, an LES filter
Filter (large eddy simulation)
Filtering in the context of large eddy simulation is a mathematical operation intended to remove a range of small scales from the solution to the Navier-Stokes equations...
is applied to the discretized Navier-Stokes equations, providing a well-defined filter shape and reducing the truncation error. However, explicit filtering requires a finer grid than implicit filtering, and the computational cost increases with
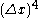. Chapter 8 of Sagaut (2006) covers LES numerics in greater detail.Modeling Unresolved Scales
To discuss the modeling of unresolved scales, first the unresolved scales must be classified. They fall into two groups: resolved sub-filter scales (SFS), and sub-grid scales(SGS).The resolved sub-filter scales represent the scales with wave numbers larger than the cutoff wave number
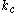, but whose effects are dampened by the filter. Resolved sub-filter scales only exist when filters non-local in wave-space are used (such as a box or Gaussian filter). These resolved sub-filter scales must be modeled using filter reconstruction.Sub-grid scales are any scales that are smaller than the cutoff filter width
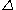. The form of the SGS model depends on the filter implementation. As mentioned in the Numerical methods for LES section, if the filter is implicit, there is no SGS model implemented. Only explicit filters require SGS models.Sub-grid scale models
Without a universally valid description of turbulence, some empirical information must be utilized when constructing and applying SGS models. Two classes of SGS models exist; the first class is functional models and the second class is structural models. Some models may be categorized as both.Functional (Eddy-Viscosity) Models
Functional models are simpler than structural models, focusing only on dissipating energy at a rate that is physically correct. These are based on an artificial eddy viscosity approach, where the effects of turbulence are lumped into a turbulent viscosity. The approach treats dissipation of kinetic energy at sub-grid scales as analogous to molecular diffusion. In this case, the deviatoric part of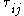 is modeled as: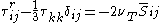where
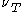is the turbulent eddy viscosity and 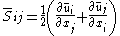is the rate-of-strain tensor.Based on dimensional analysis, the eddy viscosity must have units of
. Most eddy viscosity SGS models model the eddy viscosity as the product of a characteristic length scale and a characteristic velocity scale.Smagorinsky-Lilly model
The first SGS model developed was the Smagorinsky-Lilly SGS model, which was developed by SmagorinskyJoseph Smagorinsky
Joseph Smagorinsky was an American meteorologist and the first director of the National Oceanic and Atmospheric Administration's Geophysical Fluid Dynamics Laboratory.- Early life :...
and used in the first LES simulation by Deardorff. It models the eddy viscosity as:
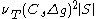
where
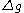is the grid size and 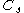is a constant.This method assumes that the energy production and dissipation of the small scales are in equilibrium - that is,
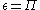.Germano dynamic model
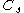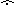Germano et al. identified a number of studies using the Smagorinsky model that each found different values for the Smagorinsky constant for different flow configurations. In an attempt to formulate a more universal approach to SGS models, Germano et al. proposed a dynamic Smagorinsky model, which utilized two filters: a grid LES filter, denoted , and a test LES filter, denoted . In this case, the resolved turbulent stress tensor 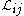is defined aswhich is also called the Germano identity. The quantity
is the residual stress tensor for the test filter, and is the residual stress tensor for the grid filter. represents the contribution to the SGS stresses by length scales smaller than the test filter width 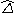but larger than the grid filter width 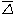. This allows the value of the Smagorinsky model to adapt to the instantaneous state of the flow.The dynamic SGS model yields an equation for
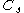:where
and 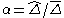. However, this procedure was numerically unstable, and additionally finding the value of 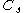was complicated by the fact that it was an overdetermined problem (one equation with five unknowns).Because of these issues, Germano enforced the dynamic constant in an average sense, so that the equation for
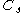was actually:Lilly proposed a modification to the dynamic model that utilized a least squares method to find
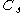, making the former version more stable and making the method more applicable.Derivation
In Einstein notationEinstein notation
In mathematics, especially in applications of linear algebra to physics, the Einstein notation or Einstein summation convention is a notational convention useful when dealing with coordinate formulae...
, the Navier-Stokes equations for an incompressible fluid are
-
-
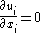
Filtering the momentum equation results in-
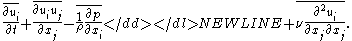
If we assume that filtering and differentiation commute, then-
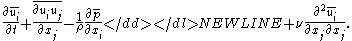
This equation models the changes in time of the filtered variables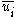
. Since the unfiltered variables 
are not known, it is impossible to directly calculate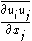 
. However, the quantity 
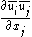is known. A substitution is made:
-
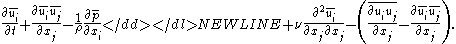
Let
. The resulting set of equations are the LES equations:
Recent applications
A few recent applications of the large eddy simulation technique include some geophysical flows including breaking waves and tidal bores. Large eddy simulation has also been used to study turbulence in the planetary boundary layer.
See also
- Direct numerical simulationDirect numerical simulationA direct numerical simulation is a simulation in computational fluid dynamics in which the Navier-Stokes equations are numerically solved without any turbulence model...
- Fluid mechanicsFluid mechanicsFluid mechanics is the study of fluids and the forces on them. Fluid mechanics can be divided into fluid statics, the study of fluids at rest; fluid kinematics, the study of fluids in motion; and fluid dynamics, the study of the effect of forces on fluid motion...
- Galilean invarianceGalilean invarianceGalilean invariance or Galilean relativity is a principle of relativity which states that the fundamental laws of physics are the same in all inertial frames...
- an important property of certain types of filters - Reynolds-averaged Navier–Stokes equations
- TurbulenceTurbulenceIn fluid dynamics, turbulence or turbulent flow is a flow regime characterized by chaotic and stochastic property changes. This includes low momentum diffusion, high momentum convection, and rapid variation of pressure and velocity in space and time...
- Direct numerical simulation
-
-
-