
Landau theory
Encyclopedia
Landau theory in physics
was introduced by Lev Landau
in an attempt to formulate a general theory of second-order phase transition
s. He was motivated to suggest that the free energy of any system should obey two conditions: that the free energy is analytic, and that it obeys the symmetry of the Hamiltonian
.
Given these two conditions, one can write down (in the vicinity of the critical temperature, Tc) a phenomenological expression for the free energy as a Taylor expansion in the order parameter. For example, the Ising model
free energy may be written as the following:

where the parameter
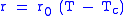
for physical reasons. The variable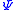 is the coarse-grained field of spins, known as the order parameter or the total magnetization.
is the coarse-grained field of spins, known as the order parameter or the total magnetization.
This theory of Landau first raised the order parameter to prominence. Note that the Ising model exhibits the following discrete symmetry: If every spin in the model is flipped, such that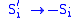 , where
, where 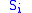 is the value of the
is the value of the 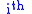 spin, the Hamiltonian (and consequently the free energy) remains unchanged. This symmetry is reflected in the even powers of
spin, the Hamiltonian (and consequently the free energy) remains unchanged. This symmetry is reflected in the even powers of 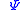 in
in 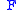 .
.
Landau theory has been extraordinarily useful. While the exact values of the parameters and
and  were unknown, critical exponents could still be calculated with ease, and only depend on the original assumptions of symmetry and analyticity. For the Ising model case, the equilibrium magnetization
were unknown, critical exponents could still be calculated with ease, and only depend on the original assumptions of symmetry and analyticity. For the Ising model case, the equilibrium magnetization 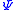 assumes the following value below the critical temperature
assumes the following value below the critical temperature  :
:

At the time, it was known experimentally that the liquid-gas coexistence curve and the ferromagnet magnetization curve both exhibited a scaling relation of the form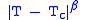 , where
, where 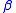 was mysteriously the same for both systems. This is the phenomenon of universality
was mysteriously the same for both systems. This is the phenomenon of universality
. It was also known that simple liquid-gas models are exactly mappable to simple magnetic models, which implied that the two systems possess the same symmetries. It then followed from Landau theory why these two apparently disparate systems should have the same critical exponents, despite having different microscopic parameters. It is now known that the phenomenon of universality
arises for other reasons (see Renormalization group
). In fact, Landau theory predicts the incorrect critical exponents for the Ising and liquid-gas systems.
The great virtue of Landau theory is that it makes specific predictions for what kind of non-analytic behavior one should see when the underlying free energy is analytic. Then, all the non-analyticity at the critical point, the critical exponents, are because the equilibrium value of the order parameter changes non-analytically, as a square root, whenever the free energy loses its unique minimum.
The extension of Landau theory to include fluctuations in the order parameter shows that Landau theory is only strictly valid near the critical points of ordinary systems with spatial dimensions of higher than 4. This is the upper critical dimension, and it can be much higher than four in more finely tuned phase transition. In Mukhamel's analysis of the isotropic Lifschitz point, the critical dimension is 8. This is because Landau theory is a mean field theory
.
This theory does not explain all the non-analyticity at the critical point, but when applied to superfluid and superconductor phase transition, Landau's theory provided inspiration for another theory, the Ginzburg-Landau theory
of superconductivity
.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
was introduced by Lev Landau
Lev Landau
Lev Davidovich Landau was a prominent Soviet physicist who made fundamental contributions to many areas of theoretical physics...
in an attempt to formulate a general theory of second-order phase transition
Phase transition
A phase transition is the transformation of a thermodynamic system from one phase or state of matter to another.A phase of a thermodynamic system and the states of matter have uniform physical properties....
s. He was motivated to suggest that the free energy of any system should obey two conditions: that the free energy is analytic, and that it obeys the symmetry of the Hamiltonian
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
.
Given these two conditions, one can write down (in the vicinity of the critical temperature, Tc) a phenomenological expression for the free energy as a Taylor expansion in the order parameter. For example, the Ising model
Ising model
The Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
free energy may be written as the following:

where the parameter
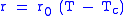
for physical reasons. The variable
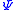 is the coarse-grained field of spins, known as the order parameter or the total magnetization.
is the coarse-grained field of spins, known as the order parameter or the total magnetization.This theory of Landau first raised the order parameter to prominence. Note that the Ising model exhibits the following discrete symmetry: If every spin in the model is flipped, such that
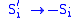 , where
, where 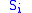 is the value of the
is the value of the 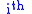 spin, the Hamiltonian (and consequently the free energy) remains unchanged. This symmetry is reflected in the even powers of
spin, the Hamiltonian (and consequently the free energy) remains unchanged. This symmetry is reflected in the even powers of 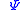 in
in 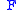 .
.Landau theory has been extraordinarily useful. While the exact values of the parameters
 and
and  were unknown, critical exponents could still be calculated with ease, and only depend on the original assumptions of symmetry and analyticity. For the Ising model case, the equilibrium magnetization
were unknown, critical exponents could still be calculated with ease, and only depend on the original assumptions of symmetry and analyticity. For the Ising model case, the equilibrium magnetization 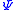 assumes the following value below the critical temperature
assumes the following value below the critical temperature  :
:
At the time, it was known experimentally that the liquid-gas coexistence curve and the ferromagnet magnetization curve both exhibited a scaling relation of the form
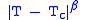 , where
, where 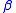 was mysteriously the same for both systems. This is the phenomenon of universality
was mysteriously the same for both systems. This is the phenomenon of universalityPhase transition
A phase transition is the transformation of a thermodynamic system from one phase or state of matter to another.A phase of a thermodynamic system and the states of matter have uniform physical properties....
. It was also known that simple liquid-gas models are exactly mappable to simple magnetic models, which implied that the two systems possess the same symmetries. It then followed from Landau theory why these two apparently disparate systems should have the same critical exponents, despite having different microscopic parameters. It is now known that the phenomenon of universality
Phase transition
A phase transition is the transformation of a thermodynamic system from one phase or state of matter to another.A phase of a thermodynamic system and the states of matter have uniform physical properties....
arises for other reasons (see Renormalization group
Renormalization group
In theoretical physics, the renormalization group refers to a mathematical apparatus that allows systematic investigation of the changes of a physical system as viewed at different distance scales...
). In fact, Landau theory predicts the incorrect critical exponents for the Ising and liquid-gas systems.
The great virtue of Landau theory is that it makes specific predictions for what kind of non-analytic behavior one should see when the underlying free energy is analytic. Then, all the non-analyticity at the critical point, the critical exponents, are because the equilibrium value of the order parameter changes non-analytically, as a square root, whenever the free energy loses its unique minimum.
The extension of Landau theory to include fluctuations in the order parameter shows that Landau theory is only strictly valid near the critical points of ordinary systems with spatial dimensions of higher than 4. This is the upper critical dimension, and it can be much higher than four in more finely tuned phase transition. In Mukhamel's analysis of the isotropic Lifschitz point, the critical dimension is 8. This is because Landau theory is a mean field theory
Mean field theory
Mean field theory is a method to analyse physical systems with multiple bodies. A many-body system with interactions is generally very difficult to solve exactly, except for extremely simple cases . The n-body system is replaced by a 1-body problem with a chosen good external field...
.
This theory does not explain all the non-analyticity at the critical point, but when applied to superfluid and superconductor phase transition, Landau's theory provided inspiration for another theory, the Ginzburg-Landau theory
Ginzburg-Landau theory
In physics, Ginzburg–Landau theory, named after Vitaly Lazarevich Ginzburg and Lev Landau, is a mathematical theory used to model superconductivity. It does not purport to explain the microscopic mechanisms giving rise to superconductivity...
of superconductivity
Superconductivity
Superconductivity is a phenomenon of exactly zero electrical resistance occurring in certain materials below a characteristic temperature. It was discovered by Heike Kamerlingh Onnes on April 8, 1911 in Leiden. Like ferromagnetism and atomic spectral lines, superconductivity is a quantum...
.
Further reading
- Michael C. Cross, Landau theory of second order phase transitions, http://www.pma.caltech.edu/~mcc/Ph127/b/Lecture6.pdf (Caltech statistical mechanics lecture notes).
- Yukhnovskii, I R, Phase Transitions of the Second Order - Collective Variables Method, World Scientific, 1987, ISBN 9971-50-087-6

