
Kronecker sum of discrete Laplacians
Encyclopedia
In mathematics, the Kronecker sum of discrete Laplacians, named after Leopold Kronecker
, is a discrete version of the separation of variables
for the continuous Laplacian in a rectangular cuboid domain.
in the discrete case, the multidimensional discrete Laplacian
is a Kronecker sum of 1D discrete Laplacians.
Example: 2D discrete Laplacian
Mathematically, using the Kronecker sum:
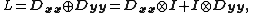
where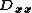 and
and 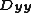 are 1D discrete Laplacians in the x- and y-directions, correspondingly, and
are 1D discrete Laplacians in the x- and y-directions, correspondingly, and 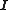 are the identities of appropriate sizes. Both
are the identities of appropriate sizes. Both  and
and  must correspond to the case of the homogeneous Dirichlet boundary condition
must correspond to the case of the homogeneous Dirichlet boundary condition
at end points of the x- and y-intervals, in order to generate the 2D discrete Laplacian L corresponding to the homogeneous Dirichlet boundary condition
everywhere on the boundary of the rectangular domain.
Here is a sample OCTAVE
/MATLAB
code to compute L on the regular 10×15 2D grid:
Eigenvalues and eigenvectors of multidimensional discrete Laplacian
Knowing all eigenvalues and eigenvectors of the factors, all eigenvalues and eigenvectors of the Kronecker product
can be explicitly calculated. Based on this, eigenvalues and eigenvectors of the Kronecker sum
can also be explicitly calculated.
The eigenvalues and eigenvectors of the standard central difference approximation of the second derivative on an interval for traditional combinations of boundary conditions at the interval end points are well known
. Combining these expressions with the formulas of eigenvalues and eigenvectors for the Kronecker sum, one can easily obtain the required answer.
Example: 3D discrete Laplacian
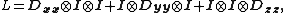
where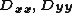 and
and 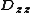 are 1D discrete Laplacians in every of the 3 directions, and
are 1D discrete Laplacians in every of the 3 directions, and 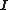 are the identities of appropriate sizes. Each 1D discrete Laplacian must correspond to the case of the homogeneous Dirichlet boundary condition
are the identities of appropriate sizes. Each 1D discrete Laplacian must correspond to the case of the homogeneous Dirichlet boundary condition
, in order to generate the 3D discrete Laplacian L corresponding to the homogeneous Dirichlet boundary condition
everywhere on the boundary. The eigenvalues are
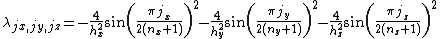
where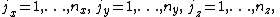 , and the corresponding eigenvectors are
, and the corresponding eigenvectors are
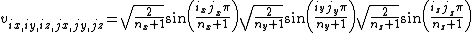
where the multi-index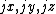 pairs the eigenvalues and the eigenvectors, while the multi-index
pairs the eigenvalues and the eigenvectors, while the multi-index
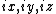 determines the location of the value of every eigenvector at the regular grid
determines the location of the value of every eigenvector at the regular grid
. The boundary points, where
the homogeneous Dirichlet boundary condition
are imposed, are just outside of the grid.
/MATLAB
code http://www.mathworks.com/matlabcentral/fileexchange/27279-laplacian-in-1d-2d-or-3d is available under a BSD License, which computes the sparse matrix of the 1, 2D, and 3D negative Laplacians on a rectangular grid for combinations of Dirichlet, Neumann, and Periodic boundary conditions using Kronecker sums of discrete 1D Laplacians. The code also provides the exact eigenvalues and eigenvectors using the explicit formulas given above.
Leopold Kronecker
Leopold Kronecker was a German mathematician who worked on number theory and algebra.He criticized Cantor's work on set theory, and was quoted by as having said, "God made integers; all else is the work of man"...
, is a discrete version of the separation of variables
Separation of variables
In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....
for the continuous Laplacian in a rectangular cuboid domain.
General form of the Kronecker sum of discrete Laplacians
In a general situation of the separation of variablesSeparation of variables
In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....
in the discrete case, the multidimensional discrete Laplacian
Discrete Laplace operator
In mathematics, the discrete Laplace operator is an analog of the continuous Laplace operator, defined so that it has meaning on a graph or a discrete grid...
is a Kronecker sum of 1D discrete Laplacians.
Example: 2D discrete LaplacianDiscrete Laplace operatorIn mathematics, the discrete Laplace operator is an analog of the continuous Laplace operator, defined so that it has meaning on a graph or a discrete grid...
on a regular gridRegular gridA regular grid is a tessellation of n-dimensional Euclidean space by congruent parallelotopes . Grids of this type appear on graph paper and may be used in finite element analysis as well as finite volume methods and finite difference methods...
with the homogeneous Dirichlet boundary conditionDirichlet boundary conditionIn mathematics, the Dirichlet boundary condition is a type of boundary condition, named after Johann Peter Gustav Lejeune Dirichlet who studied under Cauchy and succeeded Gauss at University of Göttingen. When imposed on an ordinary or a partial differential equation, it specifies the values a...
Mathematically, using the Kronecker sum: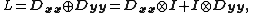
where
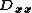 and
and 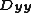 are 1D discrete Laplacians in the x- and y-directions, correspondingly, and
are 1D discrete Laplacians in the x- and y-directions, correspondingly, and 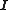 are the identities of appropriate sizes. Both
are the identities of appropriate sizes. Both  and
and  must correspond to the case of the homogeneous Dirichlet boundary condition
must correspond to the case of the homogeneous Dirichlet boundary conditionDirichlet boundary condition
In mathematics, the Dirichlet boundary condition is a type of boundary condition, named after Johann Peter Gustav Lejeune Dirichlet who studied under Cauchy and succeeded Gauss at University of Göttingen. When imposed on an ordinary or a partial differential equation, it specifies the values a...
at end points of the x- and y-intervals, in order to generate the 2D discrete Laplacian L corresponding to the homogeneous Dirichlet boundary condition
Dirichlet boundary condition
In mathematics, the Dirichlet boundary condition is a type of boundary condition, named after Johann Peter Gustav Lejeune Dirichlet who studied under Cauchy and succeeded Gauss at University of Göttingen. When imposed on an ordinary or a partial differential equation, it specifies the values a...
everywhere on the boundary of the rectangular domain.
Here is a sample OCTAVE
Octave
In music, an octave is the interval between one musical pitch and another with half or double its frequency. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music", the use of which is "common in most musical systems"...
/MATLAB
MATLAB
MATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...
code to compute L on the regular 10×15 2D grid:
- nx = 10; % number of grid points in the x-direction;
- ny = 15; % number of grid points in the y-direction;
- ex = ones(nx,1);
- Dxx = spdiags([ex -2*ex ex], [-1 0 1], nx, nx); %1D discrete Laplacian in the x-direction ;
- ey = ones(ny,1);
- Dyy = spdiags([ey, -2*ey ey], [-1 0 1], ny, ny); %1D discrete Laplacian in the y-direction ;
- L = kron(speye(ny, ny), Dxx) + kron(Dyy, speye(nx, nx)) ;
Eigenvalues and eigenvectors of multidimensional discrete LaplacianDiscrete Laplace operatorIn mathematics, the discrete Laplace operator is an analog of the continuous Laplace operator, defined so that it has meaning on a graph or a discrete grid...
on a regular gridRegular gridA regular grid is a tessellation of n-dimensional Euclidean space by congruent parallelotopes . Grids of this type appear on graph paper and may be used in finite element analysis as well as finite volume methods and finite difference methods...
Knowing all eigenvalues and eigenvectors of the factors, all eigenvalues and eigenvectors of the Kronecker productKronecker product
In mathematics, the Kronecker product, denoted by ⊗, is an operation on two matrices of arbitrary size resulting in a block matrix. It gives the matrix of the tensor product with respect to a standard choice of basis. The Kronecker product should not be confused with the usual matrix...
can be explicitly calculated. Based on this, eigenvalues and eigenvectors of the Kronecker sum
can also be explicitly calculated.
The eigenvalues and eigenvectors of the standard central difference approximation of the second derivative on an interval for traditional combinations of boundary conditions at the interval end points are well known
Eigenvalues and eigenvectors of the second derivative
Explicit formulas for eigenvalues and eigenvectors of the second derivative with different boundary conditions are provided both for the continuous and discrete cases...
. Combining these expressions with the formulas of eigenvalues and eigenvectors for the Kronecker sum, one can easily obtain the required answer.
Example: 3D discrete LaplacianDiscrete Laplace operatorIn mathematics, the discrete Laplace operator is an analog of the continuous Laplace operator, defined so that it has meaning on a graph or a discrete grid...
on a regular gridRegular gridA regular grid is a tessellation of n-dimensional Euclidean space by congruent parallelotopes . Grids of this type appear on graph paper and may be used in finite element analysis as well as finite volume methods and finite difference methods...
with the homogeneous Dirichlet boundary conditionDirichlet boundary conditionIn mathematics, the Dirichlet boundary condition is a type of boundary condition, named after Johann Peter Gustav Lejeune Dirichlet who studied under Cauchy and succeeded Gauss at University of Göttingen. When imposed on an ordinary or a partial differential equation, it specifies the values a...
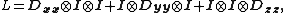
where
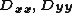 and
and 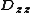 are 1D discrete Laplacians in every of the 3 directions, and
are 1D discrete Laplacians in every of the 3 directions, and 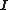 are the identities of appropriate sizes. Each 1D discrete Laplacian must correspond to the case of the homogeneous Dirichlet boundary condition
are the identities of appropriate sizes. Each 1D discrete Laplacian must correspond to the case of the homogeneous Dirichlet boundary conditionDirichlet boundary condition
In mathematics, the Dirichlet boundary condition is a type of boundary condition, named after Johann Peter Gustav Lejeune Dirichlet who studied under Cauchy and succeeded Gauss at University of Göttingen. When imposed on an ordinary or a partial differential equation, it specifies the values a...
, in order to generate the 3D discrete Laplacian L corresponding to the homogeneous Dirichlet boundary condition
Dirichlet boundary condition
In mathematics, the Dirichlet boundary condition is a type of boundary condition, named after Johann Peter Gustav Lejeune Dirichlet who studied under Cauchy and succeeded Gauss at University of Göttingen. When imposed on an ordinary or a partial differential equation, it specifies the values a...
everywhere on the boundary. The eigenvalues are
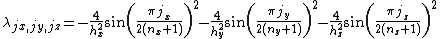
where
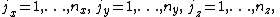 , and the corresponding eigenvectors are
, and the corresponding eigenvectors are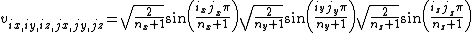
where the multi-index
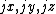 pairs the eigenvalues and the eigenvectors, while the multi-index
pairs the eigenvalues and the eigenvectors, while the multi-index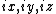 determines the location of the value of every eigenvector at the regular grid
determines the location of the value of every eigenvector at the regular gridRegular grid
A regular grid is a tessellation of n-dimensional Euclidean space by congruent parallelotopes . Grids of this type appear on graph paper and may be used in finite element analysis as well as finite volume methods and finite difference methods...
. The boundary points, where
the homogeneous Dirichlet boundary condition
Dirichlet boundary condition
In mathematics, the Dirichlet boundary condition is a type of boundary condition, named after Johann Peter Gustav Lejeune Dirichlet who studied under Cauchy and succeeded Gauss at University of Göttingen. When imposed on an ordinary or a partial differential equation, it specifies the values a...
are imposed, are just outside of the grid.
Available software
An OCTAVEOctave
In music, an octave is the interval between one musical pitch and another with half or double its frequency. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music", the use of which is "common in most musical systems"...
/MATLAB
MATLAB
MATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...
code http://www.mathworks.com/matlabcentral/fileexchange/27279-laplacian-in-1d-2d-or-3d is available under a BSD License, which computes the sparse matrix of the 1, 2D, and 3D negative Laplacians on a rectangular grid for combinations of Dirichlet, Neumann, and Periodic boundary conditions using Kronecker sums of discrete 1D Laplacians. The code also provides the exact eigenvalues and eigenvectors using the explicit formulas given above.

