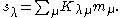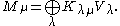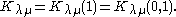Kostka number
Encyclopedia
In mathematics, a Kostka number Kλμ, introduced by , is a non-negative integer depending on two partition
s λ and μ, that is equal to the number of semistandard Young tableaux of shape λ and weight μ.
They can be used to express Schur polynomial
s sλ as a linear combination
of monomial symmetric functions mμ:
Kostka numbers also express the decomposition of the permutation module Mμ in terms of the representations Vλ corresponding to the character sλ, i.e.
On the level of representations of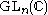 , the Kostka number Kλμ counts the dimension of the weight space corresponding to μ in the irreducible representation Vλ (where we require μ and λ to have at most n parts).
, the Kostka number Kλμ counts the dimension of the weight space corresponding to μ in the irreducible representation Vλ (where we require μ and λ to have at most n parts).
Kostka numbers are special values of the 1 or 2 variable Kostka polynomial
s:
gave tables of these numbers for partitions of numbers up to 8.
Partition (number theory)
In number theory and combinatorics, a partition of a positive integer n, also called an integer partition, is a way of writing n as a sum of positive integers. Two sums that differ only in the order of their summands are considered to be the same partition; if order matters then the sum becomes a...
s λ and μ, that is equal to the number of semistandard Young tableaux of shape λ and weight μ.
They can be used to express Schur polynomial
Schur polynomial
In mathematics, Schur polynomials, named after Issai Schur, are certain symmetric polynomials in n variables, indexed by partitions, that generalize the elementary symmetric polynomials and the complete homogeneous symmetric polynomials. In representation theory they are the characters of...
s sλ as a linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of monomial symmetric functions mμ:
Kostka numbers also express the decomposition of the permutation module Mμ in terms of the representations Vλ corresponding to the character sλ, i.e.
On the level of representations of
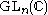 , the Kostka number Kλμ counts the dimension of the weight space corresponding to μ in the irreducible representation Vλ (where we require μ and λ to have at most n parts).
, the Kostka number Kλμ counts the dimension of the weight space corresponding to μ in the irreducible representation Vλ (where we require μ and λ to have at most n parts).Kostka numbers are special values of the 1 or 2 variable Kostka polynomial
Kostka polynomial
In mathematics, a Kostka polynomial or Kostka–Foulkes polynomial Kλμ, named after Carl Kostka, is a polynomial in two variables with non-negative integer coefficients depending on two partitions λ and μ...
s:
Examples
The Kostka numbers for partitions of size at most 3 are given by the coefficients of:- s = m = 1 (indexed by the empty partition)
- s1 = m1
- s2 = m2 + m11
- s11 = m11
- s3 = m3 + m21 + m111
- s21 = m21 + 2m111
- s111 = m111.
gave tables of these numbers for partitions of numbers up to 8.