
Komlós–Major–Tusnády approximation
Encyclopedia
In theory of probability, the Komlós–Major–Tusnády approximation (also known as the KMT approximation, the KMT embedding, or the Hungarian embedding) is an approximation of the empirical process
by a Gaussian process
constructed on the same probability space
. It is named after Hungarian mathematicians János Komlós
, Gábor Tusnády, and Péter Major.
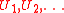 be independent uniform
be independent uniform
(0,1) random variable
s. Define a uniform empirical distribution function
as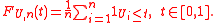
Define a uniform empirical process
as
The Donsker theorem (1952) shows that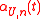 converges in law
converges in law
to a Brownian bridge
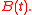 Komlós, Major and Tusnády established a sharp bound for the speed of this weak convergence.
Komlós, Major and Tusnády established a sharp bound for the speed of this weak convergence.
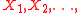 with cdf
with cdf
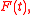 it is possible to construct a probability space where independent sequences of empirical processes
it is possible to construct a probability space where independent sequences of empirical processes 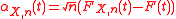 and Gaussian process
and Gaussian process
es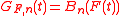 exist such that
exist such that
Empirical process
The study of empirical processes is a branch of mathematical statistics and a sub-area of probability theory. It is a generalization of the central limit theorem for empirical measures...
by a Gaussian process
Gaussian process
In probability theory and statistics, a Gaussian process is a stochastic process whose realisations consist of random values associated with every point in a range of times such that each such random variable has a normal distribution...
constructed on the same probability space
Probability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
. It is named after Hungarian mathematicians János Komlós
János Komlós (mathematician)
János Komlós is a Hungarian-American mathematician, working in probability theory and discrete mathematics. He is a professor of mathematics at Rutgers University since 1988. He graduated from the Eötvös Loránd University, then became a fellow at the Mathematical Institute of the Hungarian Academy...
, Gábor Tusnády, and Péter Major.
Theory
Let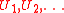 be independent uniform
be independent uniformUniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
(0,1) random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s. Define a uniform empirical distribution function
Empirical distribution function
In statistics, the empirical distribution function, or empirical cdf, is the cumulative distribution function associated with the empirical measure of the sample. This cdf is a step function that jumps up by 1/n at each of the n data points. The empirical distribution function estimates the true...
as
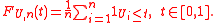
Define a uniform empirical process
Empirical process
The study of empirical processes is a branch of mathematical statistics and a sub-area of probability theory. It is a generalization of the central limit theorem for empirical measures...
as

The Donsker theorem (1952) shows that
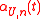 converges in law
converges in lawConvergence of random variables
In probability theory, there exist several different notions of convergence of random variables. The convergence of sequences of random variables to some limit random variable is an important concept in probability theory, and its applications to statistics and stochastic processes...
to a Brownian bridge
Brownian bridge
A Brownian bridge is a continuous-time stochastic process B whose probability distribution is the conditional probability distribution of a Wiener process W given the condition that B = B = 0.The expected value of the bridge is zero, with variance t, implying that the most...
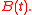 Komlós, Major and Tusnády established a sharp bound for the speed of this weak convergence.
Komlós, Major and Tusnády established a sharp bound for the speed of this weak convergence.- Theorem (KMT, 1975) On a suitable probability spaceProbability spaceIn probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
for independent uniform (0,1) r.v. the empirical process
the empirical process 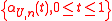 can be approximated by a sequence of Brownian bridges
can be approximated by a sequence of Brownian bridges 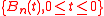 such that
such that
- for all positive integers n and all
 , where a, b, and c are positive constants.
, where a, b, and c are positive constants.
Corollary
A corollary of that theorem is that for any real iid r.v.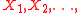 with cdf
with cdfCDF
-Mathematics, science, and computers:* .cdf , the ANDI/netCDF mass spectrometry data interchange file format* Channel Definition Format, an XML standard* Charging Data Function, in the Session Initiation Protocol standard...
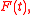 it is possible to construct a probability space where independent sequences of empirical processes
it is possible to construct a probability space where independent sequences of empirical processes 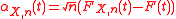 and Gaussian process
and Gaussian processGaussian process
In probability theory and statistics, a Gaussian process is a stochastic process whose realisations consist of random values associated with every point in a range of times such that each such random variable has a normal distribution...
es
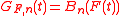 exist such that
exist such that
-
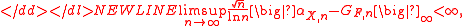 almost surelyAlmost surelyIn probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
almost surelyAlmost surelyIn probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
.


