
János Komlós (mathematician)
Encyclopedia
János Komlós is a Hungarian-American
mathematician, working in probability theory
and discrete mathematics
. He is a professor of mathematics at Rutgers University
since 1988. He graduated from the Eötvös Loránd University, then became a fellow at the Mathematical Institute
of the Hungarian Academy of Sciences
. Between 1984–1988 he worked at the University of California at San Diego.

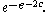
. In 1975 he received the Alfréd Rényi Prize
, a prize established for researchers of the Alfréd Rényi Institute of Mathematics
. In 1998 he was elected as an external member to the Hungarian Academy of Sciences
.
Hungarian American
Hungarian Americans Hungarian are American citizens of Hungarian descent. The constant influx of Hungarian immigrants was marked by several waves of sharp increase.-History:...
mathematician, working in probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and discrete mathematics
Discrete mathematics
Discrete mathematics is the study of mathematical structures that are fundamentally discrete rather than continuous. In contrast to real numbers that have the property of varying "smoothly", the objects studied in discrete mathematics – such as integers, graphs, and statements in logic – do not...
. He is a professor of mathematics at Rutgers University
Rutgers University
Rutgers, The State University of New Jersey , is the largest institution for higher education in New Jersey, United States. It was originally chartered as Queen's College in 1766. It is the eighth-oldest college in the United States and one of the nine Colonial colleges founded before the American...
since 1988. He graduated from the Eötvös Loránd University, then became a fellow at the Mathematical Institute
Alfréd Rényi Institute of Mathematics
The Alfréd Rényi Institute of Mathematics is the research institute in mathematics of the Hungarian Academy of Sciences. It was created in 1950 by Alfréd Rényi, who directed it until his death. Since its creation, the institute has been the center of mathematical research in Hungary. It received...
of the Hungarian Academy of Sciences
Hungarian Academy of Sciences
The Hungarian Academy of Sciences is the most important and prestigious learned society of Hungary. Its seat is at the bank of the Danube in Budapest.-History:...
. Between 1984–1988 he worked at the University of California at San Diego.
Notable results
- He proved that every L1-bounded sequence of real functions contains a subsequence such that the arithmetic meanArithmetic meanIn mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
s of all its subsequences converge pointwise almost everywhere. In probabilistic terminology, the theorem is as follows. Let ξ1,ξ2,... be a sequence of random variableRandom variableIn probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s such that E[ξ1],E[ξ2],... is bounded. Then there exist a subsequence ξ'1, ξ'2,... and a random variable β such that for each further subsequence η1,η2,... of ξ'0, ξ'1,... we have (η1+...+ηn)/n → β a.sAlmost surelyIn probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
.
- With AjtaiMiklós AjtaiMiklós Ajtai is a computer scientist at the IBM Almaden Research Center. In 2003 he received the Knuth Prize for his numerous contributions to the field, including a classic sorting network algorithm Miklós Ajtai (born 2 July 1946, Budapest, Hungary) is a computer scientist at the IBM Almaden...
and SzemerédiEndre SzemerédiEndre Szemerédi is a Hungarian mathematician, working in the field of combinatorics and theoretical computer science. He is the State of New Jersey Professor of computer science at Rutgers University since 1986...
he proved the ct2/log t upper bound for the Ramsey number R(3,t). The corresponding lower bound was proved by KimJeong Han KimJeong Han Kim is a South Korean mathematician specializing in combinatorics and computational mathematics. He studied physics and mathematical physics at Yonsei University, and earned his Ph.D in mathematics at Rutgers University...
only in 1995, this result earned him a Fulkerson PrizeFulkerson PrizeThe Fulkerson Prize for outstanding papers in the area of discrete mathematics is sponsored jointly by the Mathematical Programming Society and the American Mathematical Society . Up to three awards of $1500 each are presented at each International Symposium of the MPS...
.
- The same team of authors developed the optimal Ajtai–Komlós–Szemerédi sorting networkSorting networkA sorting network is an abstract mathematical model of a network of wires and comparator modules that is used to sort a sequence of numbers. Each comparator connects two wires and sorts the values by outputting the smaller value to one wire, and the larger to the other...
. - Komlós and SzemerédiEndre SzemerédiEndre Szemerédi is a Hungarian mathematician, working in the field of combinatorics and theoretical computer science. He is the State of New Jersey Professor of computer science at Rutgers University since 1986...
proved that if G is a random graphRandom graphIn mathematics, a random graph is a graph that is generated by some random process. The theory of random graphs lies at the intersection between graph theory and probability theory, and studies the properties of typical random graphs.-Random graph models:...
on n vertices with

- edges, where c is a fixed real number, then the probability that G has a Hamiltonian circuit converges to
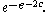
- With Gábor Sárközy and Endre SzemerédiEndre SzemerédiEndre Szemerédi is a Hungarian mathematician, working in the field of combinatorics and theoretical computer science. He is the State of New Jersey Professor of computer science at Rutgers University since 1986...
he proved the so called blow-up lemma which claims that the regular pairs in Szemerédi's regularity lemma are similar to complete bipartite graphComplete bipartite graphIn the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
s when considering the embedding of graphs with bounded degrees. - Komlós also wrote highly-cited papers on sums of random variables, space-efficient representations of sparse sets, random matricesRandom matrixIn probability theory and mathematical physics, a random matrix is a matrix-valued random variable. Many important properties of physical systems can be represented mathematically as matrix problems...
, the Szemerédi regularity lemmaSzemerédi regularity lemmaIn mathematics, the Szemerédi regularity lemma states that every large enough graph can be divided into subsets of about the same size so that the edges between different subsets behave almost randomly. introduced a weaker version of this lemma, restricted to bipartite graphs, in order to prove ...
, and derandomization.
Degrees, awards
Komlós received his Ph.D. in 1967 from Eötvös Loránd University under the supervision of Alfréd RényiAlfréd Rényi
Alfréd Rényi was a Hungarian mathematician who made contributions in combinatorics, graph theory, number theory but mostly in probability theory.-Life:...
. In 1975 he received the Alfréd Rényi Prize
Alfréd Rényi Prize
The Alfréd Rényi Prize is awarded biannually by the Alfréd Rényi Institute of Mathematics of the Hungarian Academy of Science in honor of founder Alfréd Rényi. By the current rules it is given to one or two fellows of the Institute in recognition of their outstanding performance in mathematics...
, a prize established for researchers of the Alfréd Rényi Institute of Mathematics
Alfréd Rényi Institute of Mathematics
The Alfréd Rényi Institute of Mathematics is the research institute in mathematics of the Hungarian Academy of Sciences. It was created in 1950 by Alfréd Rényi, who directed it until his death. Since its creation, the institute has been the center of mathematical research in Hungary. It received...
. In 1998 he was elected as an external member to the Hungarian Academy of Sciences
Hungarian Academy of Sciences
The Hungarian Academy of Sciences is the most important and prestigious learned society of Hungary. Its seat is at the bank of the Danube in Budapest.-History:...
.

