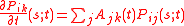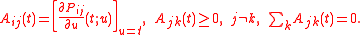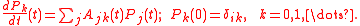Kolmogorov equations (Markov jump process)
Encyclopedia
In the context of a continuous-time Markov process, the Kolmogorov equations, including Kolmogorov forward equations and Kolmogorov backward equations, are a pair of systems of differential equation
s that describe the time-evolution of the probability
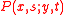 , where
, where 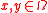 (the state space) and
(the state space) and  are the final and initial time respectively.
are the final and initial time respectively.
 in place of
in place of  .
.
Kolmogorov forward equations read
while Kolmogorov backward equations are
The functions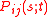 are continuous and derivable in both time arguments. They represent the
are continuous and derivable in both time arguments. They represent the
probability that the system that was in state at time
at time  jumps to state
jumps to state 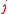 at some later time
at some later time  . The continuous quantities
. The continuous quantities 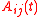 satisfy
satisfy
(Kolmogorov called it Fundamental equation) for time-continuous and differentiable Markov processes on a finite, discrete state space. In this formulation, it is assumed that the probabilities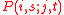 are continuous and differentiable functions of
are continuous and differentiable functions of  . Also adequate limit properties for the derivatives are assumed. Feller derives the equations under slightly different conditions, starting with the concept of purely discontinuous Markov process and formulating them for more general state spaces. Feller proves the existence of solutions of probabilistic character to the Kolmogorov forward equations and Kolmogorov backward equations under natural conditions.
. Also adequate limit properties for the derivatives are assumed. Feller derives the equations under slightly different conditions, starting with the concept of purely discontinuous Markov process and formulating them for more general state spaces. Feller proves the existence of solutions of probabilistic character to the Kolmogorov forward equations and Kolmogorov backward equations under natural conditions.
 and assuming that the system initially is found in state
and assuming that the system initially is found in state
 , The Kolmogorov forward equations describe an initial value problem for finding the probabilities of the process, given the quantities
, The Kolmogorov forward equations describe an initial value problem for finding the probabilities of the process, given the quantities 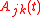 . We put
. We put 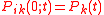 and
and
For the case of a pure death process with constant rates the only nonzero coefficients are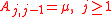 . Letting
. Letting
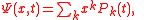
the system of equations can in this case be recast as a partial differential equation
for with initial condition
with initial condition 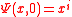 . After some manipulations, the system of equations reads,
. After some manipulations, the system of equations reads,
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s that describe the time-evolution of the probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
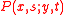 , where
, where 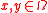 (the state space) and
(the state space) and  are the final and initial time respectively.
are the final and initial time respectively.The equations
For the case of denumerable state space we put in place of
in place of  .
.Kolmogorov forward equations read
while Kolmogorov backward equations are
The functions
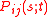 are continuous and derivable in both time arguments. They represent the
are continuous and derivable in both time arguments. They represent theprobability that the system that was in state
 at time
at time  jumps to state
jumps to state 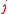 at some later time
at some later time  . The continuous quantities
. The continuous quantities 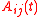 satisfy
satisfyBackground
The original derivation of the equations by Kolmogorov starts with the Chapman-Kolmogorov equationChapman-Kolmogorov equation
In mathematics, specifically in probability theory and in particular the theory of Markovian stochastic processes, the Chapman–Kolmogorov equation is an identity relating the joint probability distributions of different sets of coordinates on a stochastic process...
(Kolmogorov called it Fundamental equation) for time-continuous and differentiable Markov processes on a finite, discrete state space. In this formulation, it is assumed that the probabilities
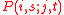 are continuous and differentiable functions of
are continuous and differentiable functions of  . Also adequate limit properties for the derivatives are assumed. Feller derives the equations under slightly different conditions, starting with the concept of purely discontinuous Markov process and formulating them for more general state spaces. Feller proves the existence of solutions of probabilistic character to the Kolmogorov forward equations and Kolmogorov backward equations under natural conditions.
. Also adequate limit properties for the derivatives are assumed. Feller derives the equations under slightly different conditions, starting with the concept of purely discontinuous Markov process and formulating them for more general state spaces. Feller proves the existence of solutions of probabilistic character to the Kolmogorov forward equations and Kolmogorov backward equations under natural conditions.Relation with the generating function
Still in the discrete state case, letting and assuming that the system initially is found in state
and assuming that the system initially is found in state , The Kolmogorov forward equations describe an initial value problem for finding the probabilities of the process, given the quantities
, The Kolmogorov forward equations describe an initial value problem for finding the probabilities of the process, given the quantities 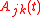 . We put
. We put 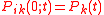 and
andFor the case of a pure death process with constant rates the only nonzero coefficients are
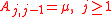 . Letting
. Letting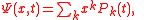
the system of equations can in this case be recast as a partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
for
 with initial condition
with initial condition 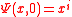 . After some manipulations, the system of equations reads,
. After some manipulations, the system of equations reads,External links
- Continuous-time Markov process
- Master equationMaster equationIn physics and chemistry and related fields, master equations are used to describe the time-evolution of a system that can be modelled as being in exactly one of countable number of states at any given time, and where switching between states is treated probabilistically...
- Fokker–Planck equation
- Kolmogorov backward equations (diffusion)