Kantorovich inequality
Encyclopedia
In mathematics
, the Kantorovich inequality is a particular case of the Cauchy-Schwarz inequality, which is itself a generalization of the triangle inequality
.
The triangle inequality states that the length of two sides of any triangle, added together, will be equal to or greater than the length of the third side. In simplest terms, the Kantorovich inequality translates the basic idea of the triangle inequality into the terms and notational conventions of linear programming
. (See vector space
, inner product, and normed vector space
for other examples of how the basic ideas inherent in the triangle inequality--line segment and distance--can be generalized into a broader context.)
More formally, the Kantorovich inequality can be expressed this way:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Kantorovich inequality is a particular case of the Cauchy-Schwarz inequality, which is itself a generalization of the triangle inequality
Triangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
.
The triangle inequality states that the length of two sides of any triangle, added together, will be equal to or greater than the length of the third side. In simplest terms, the Kantorovich inequality translates the basic idea of the triangle inequality into the terms and notational conventions of linear programming
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
. (See vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
, inner product, and normed vector space
Normed vector space
In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
for other examples of how the basic ideas inherent in the triangle inequality--line segment and distance--can be generalized into a broader context.)
More formally, the Kantorovich inequality can be expressed this way:
- Let
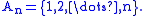
- Then
-
-

The Kantorovich inequality is used in convergence analysis; it bounds the convergence rate of Cauchy's steepest descent.
Equivalents of the Kantorovich inequality have arisen in a number of different fields. For instance, the Bunyakovsky inequality, the Wielandt inequality, and the Cauchy–Schwarz inequality are equivalent to the Kantorovich inequality and all of these are, in turn, special cases of the Hölder inequality.
The Kantorovich inequality is named after Soviet economist, mathematician, and Nobel PrizeNobel PrizeThe Nobel Prizes are annual international awards bestowed by Scandinavian committees in recognition of cultural and scientific advances. The will of the Swedish chemist Alfred Nobel, the inventor of dynamite, established the prizes in 1895...
winner Leonid KantorovichLeonid KantorovichLeonid Vitaliyevich Kantorovich was a Soviet mathematician and economist, known for his theory and development of techniques for the optimal allocation of resources...
, a pioneer in the field of linear programmingLinear programmingLinear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
.
External links
-