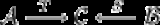
Comma category
Encyclopedia
In mathematics, a comma category (a special case being a slice category) is a construction in category theory
. It provides another way of looking at morphism
s: instead of simply relating objects of a category
to one another, morphisms become objects in their own right. This notion was introduced in 1963 by F. W. Lawvere
, although the technique did not become generally known until many years later. Today, it has become particularly important to mathematicians, because several important mathematical concepts can be treated as comma categories. There are also certain guarantees about the existence of limit
s and colimits in the context of comma categories. The name comes from the notation originally used by Lawvere, which involved the comma
punctuation mark. Although standard notation has changed since the use of a comma as an operator is potentially confusing, and even Lawvere dislikes the uninformative term "comma category", the name persists.
s with the same codomain. Often one of these will have domain 1 (the one-object one-morphism category). Some accounts of category theory consider these special cases only, but the term comma category is actually much more general.
, 
, and 
are categories, and 
and 
are functor
s
We can form the comma category
as follows:
Morphisms are composed by taking 
to be 
, whenever the latter expression is defined. The identity morphism on an object 
is 
.
, 
is the identity functor, and 
(the category with one object 
and one morphism). Then 
for some object 
in 
. In this case, the comma category is written 
, and is often called the slice category over 
or the category of objects over 
. The objects 
can be simplified to pairs 
, where 
. Sometimes, 
is denoted 
. A morphism from 
to 
in the slice category is then an arrow 
making the following diagram commute:
concept to a slice category is a coslice category. Here,
has domain 1 and 
is an identity functor. In this case, the comma category is often written
, where 
is the object of 
selected by 
. It is called the coslice category with respect to 
, or the category of objects under 
. The objects are pairs 
with 
. Given 
and 
, a morphism in the coslice category is a map 
making the following diagram commute:
and 
are identity functors on 
(so 
). In this case, the comma category is the arrow category 
. Its objects are the morphisms of 
, and its morphisms are commuting squares in 
.
is the forgetful functor
mapping an abelian group
to its underlying set, and
is some fixed set (regarded as a functor from 1), then the comma category 
has objects that are maps from 
to a set underlying a group. This relates to the left adjoint of 
, which is the functor that maps a set to the free abelian group
having that set as its basis. In particular, the initial object of
is the canonical injection 
, where 
is the free group generated by 
.
An object of
is called a morphism from 
to 
or a 
-structured arrow with domain 
in. An object of 
is called a morphism from 
to 
or a 
-costructured arrow with codomain 
in.
Another special case occurs when both
and 
are functors with domain 1. If 
and 
, then the comma category 
, written 
, is the discrete category
whose objects are morphisms from
to 
.
in comma categories may be "inherited". If
and 
are cocomplete, 
is a cocontinuous functor, and 
another functor (not necessarily cocontinuous), then the comma category 
produced will also be cocomplete. For example, in the above construction of the category of graphs, the category of sets is cocomplete, and the identity functor is cocontinuous: so graphs are also cocomplete - all (small) colimits exist. This result is much harder to obtain directly.
If
and 
are complete, and both 
and 
are continuous functors, then the comma category 
is also complete, and the projection functors 
and 
are limit preserving.
The notion of a universal morphism
to a particular colimit, or from a limit, can be expressed in terms of a comma category. Essentially, we create a category whose objects are cones, and where the limiting cone is a terminal object; then, each universal morphism for the limit is just the morphism to the terminal object. This works in the dual case, with a category of cocones having an initial object. For example, let
be a category with 
the functor taking each object 
to 
and each arrow 
to 
. A universal morphism from 
to 
consists, by definition, of an object 
and morphism 
with the universal property that for any morphism 
there is a unique morphism 
with 
. In other words, it is an object in the comma category 
having a morphism to any other object in that category; it is initial. This serves to define the coproduct
in
, when it exists.
and 
are adjoint
if and only if the comma categories
and 
, with 
and 
the identity functors on 
and 
respectively, are isomorphic, and equivalent elements in the comma category can be projected onto the same element of 
. This allows adjunctions to be described without involving sets, and was in fact the original motivation for introducing comma categories.
are equal, then the diagram which defines morphisms in 
with 
is identical to the diagram which defines a natural transformation
. The difference between the two notions is that a natural transformation is a particular collection of morphisms of type of the form 
, while objects of the comma category contains all morphisms of type of such form. A functor to the comma category selects that particular collection of morphisms. This is described succinctly by an observation by Huq that a natural transformation 
, with 
, corresponds to a functor 
which maps each object 
to 
and maps each morphism 
to 
. This is a bijective
correspondence between natural transformations
and functors 
which are sections
of both forgetful functors from
.
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
. It provides another way of looking at morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s: instead of simply relating objects of a category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
to one another, morphisms become objects in their own right. This notion was introduced in 1963 by F. W. Lawvere
William Lawvere
Francis William Lawvere is a mathematician known for his work in category theory, topos theory and the philosophy of mathematics.-Biography:...
, although the technique did not become generally known until many years later. Today, it has become particularly important to mathematicians, because several important mathematical concepts can be treated as comma categories. There are also certain guarantees about the existence of limit
Limit (category theory)
In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products and inverse limits....
s and colimits in the context of comma categories. The name comes from the notation originally used by Lawvere, which involved the comma
Comma
A comma is a type of punctuation mark . The word comes from the Greek komma , which means something cut off or a short clause.Comma may also refer to:* Comma , a type of interval in music theory...
punctuation mark. Although standard notation has changed since the use of a comma as an operator is potentially confusing, and even Lawvere dislikes the uninformative term "comma category", the name persists.
Definition
The most general comma category construction involves two functorFunctor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
s with the same codomain. Often one of these will have domain 1 (the one-object one-morphism category). Some accounts of category theory consider these special cases only, but the term comma category is actually much more general.
General form
Suppose that, , and are categories, and and are functorFunctor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
s
We can form the comma category
as follows:
- The objects are all triples
with 
an object in 
, 
an object in 
, and 
a morphism in 
. - The morphisms from
to 
are all pairs 
where 
and 
are morphisms in 
and 
respectively, such that the following diagram commutesCommutative diagramIn mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
:
to be , whenever the latter expression is defined. The identity morphism on an object is .Slice category
The first special case occurs when, is the identity functor, and (the category with one object and one morphism). Then for some object in . In this case, the comma category is written , and is often called the slice category over or the category of objects over . The objects can be simplified to pairs , where . Sometimes, is denoted . A morphism from to in the slice category is then an arrow making the following diagram commute:Coslice category
The dualDual (category theory)
In category theory, a branch of mathematics, duality is a correspondence between properties of a category C and so-called dual properties of the opposite category Cop...
concept to a slice category is a coslice category. Here,
has domain 1 and is an identity functor. In this case, the comma category is often written, where is the object of selected by . It is called the coslice category with respect to , or the category of objects under . The objects are pairs with . Given and , a morphism in the coslice category is a map making the following diagram commute:Arrow category
and are identity functors on (so ). In this case, the comma category is the arrow category . Its objects are the morphisms of , and its morphisms are commuting squares in .Other variations
In the case of the slice or coslice category, the identity functor may be replaced with some other functor; this yields a family of categories particularly useful in the study of adjoint functors. For example, if is the forgetful functorForgetful functor
In mathematics, in the area of category theory, a forgetful functor is a type of functor. The nomenclature is suggestive of such a functor's behaviour: given some object with structure as input, some or all of the object's structure or properties is 'forgotten' in the output...
mapping an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
to its underlying set, and
is some fixed set (regarded as a functor from 1), then the comma category has objects that are maps from to a set underlying a group. This relates to the left adjoint of , which is the functor that maps a set to the free abelian groupFree abelian group
In abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
having that set as its basis. In particular, the initial object of
is the canonical injection , where is the free group generated by .An object of
is called a morphism from to or a -structured arrow with domain in. An object of is called a morphism from to or a -costructured arrow with codomain in.Another special case occurs when both
and are functors with domain 1. If and , then the comma category , written , is the discrete categoryDiscrete category
In mathematics, especially category theory, a discrete category is a category whose only morphisms are the identity morphisms. It is the simplest kind of category...
whose objects are morphisms from
to .Properties
For each comma category there are forgetful functors from it.- Domain functor,
, which maps:
- objects:
; - morphisms:
;
- objects:
- Codomain functor,
, which maps:
- objects:
; - morphisms:
.
- objects:
Some notable categories
Several interesting categories have a natural definition in terms of comma categories.- The category of pointed setPointed setIn mathematics, a pointed set is a set X with a distinguished element x_0\in X, which is called the basepoint. Maps of pointed sets are those functions that map one basepoint to another, i.e. a map f : X \to Y such that f = y_0. This is usually denotedf : \to .Pointed sets may be regarded as a...
s is a comma category,
with 
being (a functor selecting) any singleton set, and 
(the identity functor of) the category of setsCategory of setsIn the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
. Each object of this category is a set, together with a function selecting some element of the set: the "basepoint". Morphisms are functions on sets which map basepoints to basepoints. In a similar fashion one can form the category of pointed spacePointed spaceIn mathematics, a pointed space is a topological space X with a distinguished basepoint x0 in X. Maps of pointed spaces are continuous maps preserving basepoints, i.e. a continuous map f : X → Y such that f = y0...
s
. - The category of graphsGraph (mathematics)In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
is
, with 
the functor taking a set 
to 
. The objects 
then consist of two sets and a function; 
is an indexing set, 
is a set of nodes, and 
chooses pairs of elements of 
for each input from 
. That is, 
picks out certain edges from the set 
of possible edges. A morphism in this category is made up of two functions, one on the indexing set and one on the node set. They must "agree" according to the general definition above, meaning that 
must satisfy 
. In other words, the edge corresponding to a certain element of the indexing set, when translated, must be the same as the edge for the translated index. - Many "augmentation" or "labelling" operations can be expressed in terms of comma categories. Let
be the functor taking each graph to the set of its edges, and let 
be (a functor selecting) some particular set: then 
is the category of graphs whose edges are labelled by elements of 
. This form of comma category is often called objects 
-over 
- closely related to the "objects over 
" discussed above. Here, each object takes the form 
, where 
is a graph and 
a function from the edges of 
to 
. The nodes of the graph could be labelled in essentially the same way. - A category is said to be locally cartesian closed if every slice of it is cartesian closed (see above for the notion of slice). Locally cartesian closed categories are the classifying categories of dependent type theories.
Limits and universal morphisms
ColimitsLimit (category theory)
In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products and inverse limits....
in comma categories may be "inherited". If
and are cocomplete, is a cocontinuous functor, and another functor (not necessarily cocontinuous), then the comma category produced will also be cocomplete. For example, in the above construction of the category of graphs, the category of sets is cocomplete, and the identity functor is cocontinuous: so graphs are also cocomplete - all (small) colimits exist. This result is much harder to obtain directly.If
and are complete, and both and are continuous functors, then the comma category is also complete, and the projection functors and are limit preserving.The notion of a universal morphism
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
to a particular colimit, or from a limit, can be expressed in terms of a comma category. Essentially, we create a category whose objects are cones, and where the limiting cone is a terminal object; then, each universal morphism for the limit is just the morphism to the terminal object. This works in the dual case, with a category of cocones having an initial object. For example, let
be a category with the functor taking each object to and each arrow to . A universal morphism from to consists, by definition, of an object and morphism with the universal property that for any morphism there is a unique morphism with . In other words, it is an object in the comma category having a morphism to any other object in that category; it is initial. This serves to define the coproductCoproduct
In category theory, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the...
in
, when it exists.Adjunctions
Lawvere showed that the functors and are adjointAdjoint functors
In mathematics, adjoint functors are pairs of functors which stand in a particular relationship with one another, called an adjunction. The relationship of adjunction is ubiquitous in mathematics, as it rigorously reflects the intuitive notions of optimization and efficiency...
if and only if the comma categories
and , with and the identity functors on and respectively, are isomorphic, and equivalent elements in the comma category can be projected onto the same element of . This allows adjunctions to be described without involving sets, and was in fact the original motivation for introducing comma categories.Natural transformations
If the domains of are equal, then the diagram which defines morphisms in with is identical to the diagram which defines a natural transformationNatural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
. The difference between the two notions is that a natural transformation is a particular collection of morphisms of type of the form , while objects of the comma category contains all morphisms of type of such form. A functor to the comma category selects that particular collection of morphisms. This is described succinctly by an observation by Huq that a natural transformation , with , corresponds to a functor which maps each object to and maps each morphism to . This is a bijectiveBijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
correspondence between natural transformations
and functors which are sectionsSection (category theory)
In category theory, a branch of mathematics, a section is a right inverse of a morphism. Dually, a retraction is a left inverse...
of both forgetful functors from
.