
Kaczmarz method
Encyclopedia
The Kaczmarz method, based on the work of the Polish
mathematican Stefan Kaczmarz
,
is a method for solving linear system
s of equations .
.
It was rediscovered in the field of image reconstruction from projections by
Richard Gordon
, Robert Bender, and Gabor Herman
in 1970, where it is called
the Algebraic Reconstruction Technique
(ART)
.
It is applicable to any linear system of equations, but its computational
advantage relative to other methods depends on the system being sparse. This
method has been found efficacious in the area of image reconstruction from
projections, especially when "blobs" are chosen as the basis function
s.
It has been demonstrated to be superior, in some biomedical imaging applications,
to other methods such as the filtered backprojection method
.
The Kaczmarz method or ART is an iterative algorithm that has
many applications ranging from computed tomography
(CT) to
signal processing
. It can be obtained also by applying to the hyperplanes,
described by the linear system, the method of successive projections onto convex
sets (POCS)
,
.
Given a real or complex

matrix
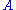
and a real or complex vector
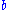 ,
,
respectively, the method computes an approximation of the solution of the linear
systems of equations as in the following formula,
mathematican Stefan Kaczmarz
Stefan Kaczmarz
Stefan Kaczmarz was a Polish mathematician. His Kaczmarz method provided the basis for many modern imaging technologies, including the CAT scan....
,
is a method for solving linear system
Linear system
A linear system is a mathematical model of a system based on the use of a linear operator.Linear systems typically exhibit features and properties that are much simpler than the general, nonlinear case....
s of equations
 .
.It was rediscovered in the field of image reconstruction from projections by
Richard Gordon
Richard Gordon
Richard Gordon may refer to:*Richard Gordon , English novelist, screenwriter and doctor*Richard Gordon , Jewish leader*Richard Gordon , American football player*Richard F. Gordon, Jr...
, Robert Bender, and Gabor Herman
Gabor Herman
Gabor T. Herman is a pioneer in the field of computed tomography, an important medical diagnostic procedure. He is also author of books on digital geometry and digital topology, 3D rendering in medicine and discrete tomography. He has written well over 100 research articles, including several...
in 1970, where it is called
the Algebraic Reconstruction Technique
Algebraic Reconstruction Technique
frame|right|Animated sequence of reconstruction steps, one iteration.The Algebraic Reconstruction Technique is an iterative algorithm for the reconstruction of a images from a series of angular projections , used in computed tomography...
(ART)
.
It is applicable to any linear system of equations, but its computational
advantage relative to other methods depends on the system being sparse. This
method has been found efficacious in the area of image reconstruction from
projections, especially when "blobs" are chosen as the basis function
Basis function
In mathematics, a basis function is an element of a particular basis for a function space. Every continuous function in the function space can be represented as a linear combination of basis functions, just as every vector in a vector space can be represented as a linear combination of basis...
s.
It has been demonstrated to be superior, in some biomedical imaging applications,
to other methods such as the filtered backprojection method
.
The Kaczmarz method or ART is an iterative algorithm that has
many applications ranging from computed tomography
Computed tomography
X-ray computed tomography or Computer tomography , is a medical imaging method employing tomography created by computer processing...
(CT) to
signal processing
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
. It can be obtained also by applying to the hyperplanes,
described by the linear system, the method of successive projections onto convex
sets (POCS)
,
.
Given a real or complex

matrix
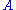
and a real or complex vector
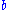 ,
,respectively, the method computes an approximation of the solution of the linear
systems of equations as in the following formula,
-
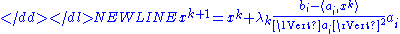
where
 ,
,
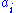
is the i-th row of the matrix
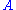 ,
,
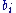
is the i-th component of the vector
 ,
,
and
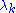
is a relaxation parameter. The above formulae gives a simple iteration routine.
There are various ways for choosing the i-th equation
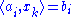
and the relaxation parameter
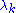
at the k-th iteration. If the linear systemLinear systemA linear system is a mathematical model of a system based on the use of a linear operator.Linear systems typically exhibit features and properties that are much simpler than the general, nonlinear case....
is
consistent, the ART converges to the minimum-norm solution, provided that the
iterations start with the zero vector, for example. There are versions of the
ART that converge to a regularized weighted least squares solution when applied
to a system of inconsistent equations and, at least as far as initial behavior
is concerned, at a lesser cost than other iterative methods, such as the
conjugate gradient methodConjugate gradient methodIn mathematics, the conjugate gradient method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix is symmetric and positive-definite. The conjugate gradient method is an iterative method, so it can be applied to sparse systems that are too...
. See Ref. and references
therein.
Recently, a randomized version of the Kaczmarz method for overdetermined linear
systems was introduced in
Ref.,
in which the i-th equation is selected with probability proportional to
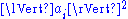 .
.
The superiority of this selection was illustrated with the reconstruction of a
bandlimited function from its nonuniformly spaced sampling values. However, it
was commented in
Ref.
that the reported success in Ref. depends on the specific
choices that were made there in translating the underlying problem, whose
geometrical nature is to find a common point of a set of hyperplanes, into a
system of algebraic equations. There will always be legitimate algebraic
representations of the underlying problem for which the selection method in
Ref. will perform in an inferior manner
Ref. Consult Ref. and
Ref.
for further discussions.

