
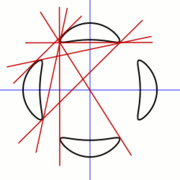
Bitangent
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a bitangent to a curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
C is a line L that touches C in two distinct points P and Q and that has the same direction to C at these points. That is, L is a tangent line at P and at Q.
Bitangents of algebraic curves
In general, an algebraic curveAlgebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
will have infinitely many secant lines, but only finitely many bitangents.
Bézout's theorem
Bézout's theorem
Bézout's theorem is a statement in algebraic geometry concerning the number of common points, or intersection points, of two plane algebraic curves. The theorem claims that the number of common points of two such curves X and Y is equal to the product of their degrees...
implies that a plane curve
Plane curve
In mathematics, a plane curve is a curve in a Euclidean plane . The most frequently studied cases are smooth plane curves , and algebraic plane curves....
with a bitangent must have degree at least 4. The case of the 28 bitangents of a quartic was a celebrated piece of geometry of the nineteenth century, a relationship being shown to the 27 lines on the cubic surface
Cubic surface
A cubic surface is a projective variety studied in algebraic geometry. It is an algebraic surface in three-dimensional projective space defined by a single polynomial which is homogeneous of degree 3...
.
Bitangents of polygons
The four bitangents of two disjoint convex polygonConvex polygon
In geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set...
s may be found efficiently by an algorithm based on binary search in which one maintains a binary search pointer into the lists of edges of each polygon and moves one of the pointers left or right at each steps depending on where the tangent lines to the edges at the two pointers cross each other. This bitangent calculation is a key subroutine in data structures for maintaining convex hull
Convex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
s dynamically
Dynamic convex hull
The dynamic convex hull problem is a class of dynamic problems in computational geometry. The problem consists in the maintenance, i.e., keeping track, of the convex hull for the dynamically changing input data, i.e., when input data elements may be inserted, deleted, or modified...
. describe an algorithm for efficiently listing all bitangent line segments that do not cross any of the other curves in a system of multiple disjoint convex curves, using a technique based on pseudotriangulation.
Bitangents may be used to speed up the visibility graph
Visibility graph
In computational geometry and robot motion planning, a visibility graph is a graph of intervisible locations, typically for a set of points and obstacles in the Euclidean plane. Each node in the graph represents a point location, and each edge represents a visible connection between them...
approach to solving the Euclidean shortest path
Euclidean shortest path
The Euclidean shortest path problem is a problem in computational geometry: given a set of polyhedral obstacles in a Euclidean space, and two points, find the shortest path between the points that does not intersect any of the obstacles....
problem: the shortest path among a collection of polygonal obstacles may only enter or leave the boundary of an obstacle along one of its bitangents, so the shortest path can be found by applying Dijkstra's algorithm
Dijkstra's algorithm
Dijkstra's algorithm, conceived by Dutch computer scientist Edsger Dijkstra in 1956 and published in 1959, is a graph search algorithm that solves the single-source shortest path problem for a graph with nonnegative edge path costs, producing a shortest path tree...
to a subgraph of the visibility graph formed by the visibility edges that lie on bitangent lines .
Related concepts
A bitangent differs from a secant lineSecant line
A secant line of a curve is a line that intersects two points on the curve. The word secant comes from the Latin secare, to cut.It can be used to approximate the tangent to a curve, at some point P...
in that a secant line may cross the curve at the two points it intersects it.
One can also consider bitangents that are not lines; for instance, the symmetry set
Symmetry set
In geometry, the symmetry set is a method for representing the local symmetries of a curve, and can be used as a method for representing the shape of objects by finding the topological skeleton...
of a curve is the locus of centers of circles that are tangent to the curve in two points.
Bitangents to pairs of circles figure prominently in Jakob Steiner
Jakob Steiner
Jakob Steiner was a Swiss mathematician who worked primarily in geometry.-Personal and professional life:...
's 1826 construction of the malfatti circles
Malfatti circles
In geometry, the Malfatti circles are three circles inside a given triangle such that each circle is tangent to the other two and to two sides of the triangle...
and in the belt problem
Belt problem
The belt problem is a mathematics problem which requires finding the length of a crossed belt that connects two circular pulleys with radius r1 and r2 whose centers are separated by a distance P...
of calculating the length of a belt connecting two pulleys.

