Jordan algebra
Encyclopedia
In abstract algebra
, a Jordan algebra is an (not necessarily associative) algebra over a field
whose multiplication
satisfies the following axioms:
The product of two elements x and y in a Jordan algebra is also denoted x ∘ y, particularly to avoid confusion with the product of a related associative algebra
.
Jordan algebras were first introduced by to formalize the notion of an algebra of observable
s in quantum mechanics
. They were originally called "r-number systems", but were renamed "Jordan algebras" by , who began the systematic study of general Jordan algebras.
A (not of characteristic
2), one can construct a Jordan algebra A+ using the same underlying addition vector space. Notice first that an associative algebra is a Jordan algebra if and only if it is commutative. If it is not commutative we can define a new multiplication on A to make it commutative, and in fact make it a Jordan algebra. The new multiplication x ∘ y is as follows: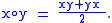
This defines a Jordan algebra A+, and we call these Jordan algebras, as well as any subalgebras of these Jordan algebras, special Jordan algebras. All other Jordan algebras are called exceptional Jordan algebras. The Shirshov–Cohn theorem states that any Jordan algebra with two generators
is special. Related to this, Macdonald's theorem states that any polynomial in three variables, which has degree one in one of the variables, and which vanishes in every special Jordan algebra, vanishes in every Jordan algebra.
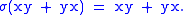
Thus the set of all elements fixed by the involution (sometimes called the hermitian elements) form a subalgebra of A+ which is sometimes denoted H(A,σ).
real, complex, or quaternionic matrices with multiplication
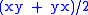
form a special Jordan algebra.
2. The set of 3×3 self-adjoint matrices over the non-associative octonion
s, again with multiplication
,
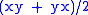is a 27 dimensional, exceptional Jordan algebra. Its automorphism group is related to the exceptional Lie group F₄. Since over the real numbers this is the only exceptional Jordan algebra, it is often referred to as "the" exceptional Jordan algebra. It was the first example of an Albert algebra
.
of a Jordan algebra A is an endomorphism D of A such that D(xy) = D(x)y+xD(y). The derivations form a Lie algebra
der(A). The Jordan identity implies that if x and y are elements of A, then the endomorphism sending z to x(yz)−y(xz) is a derivation. Thus the direct sum of A and der(A) can be made into a Lie algebra, called the structure algebra of A, str(A).
A simple example is provided by the Hermitian Jordan algebras H(A,σ). In this case any element x of A with σ(x)=−x defines a derivation. In many important examples, the structure algebra of H(A,σ) is A.
Derivation and structure algebras also form part of Tits' construction of the Freudenthal magic square
.
Not every Jordan algebra is formally real, but classified the finite dimensional formally real Jordan algebras. Every formally real Jordan algebra can be written as a direct sum of so-called simple ones, which are not themselves direct sums in a nontrivial way. In finite dimensions, the simple formally real Jordan algebras come in four infinite families, together with one exceptional case:
Of these possibilities, so far it appears that nature makes use only of the n×n complex matrices as algebras of observables. However, the spin factors play a role in special relativity, and all the formally real Jordan algebras are related to projective geometry
.
classified infinite dimensional simple (and prime) Jordan algebras. They are either of Hermitian or Clifford type. In particular, the only exceptional simple (and prime) Jordan algebras are finite dimensional Albert algebra
s, which have dimension 27.
that respects the Jordan identity.
They include several families and some exceptional algebras notably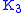
and 
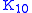
so the only eigenvalues of R are 0, 1/2, 1. If the Jordan algebra A is finite-dimensional over a field of characteristic not 2, this implies that it is a direct sum of subspaces A = A0(e) ⊕ A1/2(e) ⊕ A1(e) of the three eigenspaces. This decomposition was introduced by and is called the Peirce decomposition
of A relative to the idempotent e.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, a Jordan algebra is an (not necessarily associative) algebra over a field
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
whose multiplication
Product (mathematics)
In mathematics, a product is the result of multiplying, or an expression that identifies factors to be multiplied. The order in which real or complex numbers are multiplied has no bearing on the product; this is known as the commutative law of multiplication...
satisfies the following axioms:
-
(commutative law) -
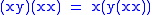(Jordan identity).
The product of two elements x and y in a Jordan algebra is also denoted x ∘ y, particularly to avoid confusion with the product of a related associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
.
Jordan algebras were first introduced by to formalize the notion of an algebra of observable
Observable
In physics, particularly in quantum physics, a system observable is a property of the system state that can be determined by some sequence of physical operations. For example, these operations might involve submitting the system to various electromagnetic fields and eventually reading a value off...
s in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. They were originally called "r-number systems", but were renamed "Jordan algebras" by , who began the systematic study of general Jordan algebras.
Special Jordan algebras
Given an associative algebraAssociative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
A (not of characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
2), one can construct a Jordan algebra A+ using the same underlying addition vector space. Notice first that an associative algebra is a Jordan algebra if and only if it is commutative. If it is not commutative we can define a new multiplication on A to make it commutative, and in fact make it a Jordan algebra. The new multiplication x ∘ y is as follows:
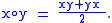
This defines a Jordan algebra A+, and we call these Jordan algebras, as well as any subalgebras of these Jordan algebras, special Jordan algebras. All other Jordan algebras are called exceptional Jordan algebras. The Shirshov–Cohn theorem states that any Jordan algebra with two generators
Generating set
In mathematics, the expressions generator, generate, generated by and generating set can have several closely related technical meanings:...
is special. Related to this, Macdonald's theorem states that any polynomial in three variables, which has degree one in one of the variables, and which vanishes in every special Jordan algebra, vanishes in every Jordan algebra.
Hermitian Jordan algebras
If (A, σ) is an associative algebra with an (anti-)involution σ, then if σ(x)=x and σ(y)=y it follows that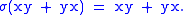Thus the set of all elements fixed by the involution (sometimes called the hermitian elements) form a subalgebra of A+ which is sometimes denoted H(A,σ).
Examples
1. The set of self-adjointSelf-adjoint
In mathematics, an element x of a star-algebra is self-adjoint if x^*=x.A collection C of elements of a star-algebra is self-adjoint if it is closed under the involution operation...
real, complex, or quaternionic matrices with multiplication
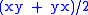
form a special Jordan algebra.
2. The set of 3×3 self-adjoint matrices over the non-associative octonion
Octonion
In mathematics, the octonions are a normed division algebra over the real numbers, usually represented by the capital letter O, using boldface O or blackboard bold \mathbb O. There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H...
s, again with multiplication
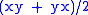,is a 27 dimensional, exceptional Jordan algebra. Its automorphism group is related to the exceptional Lie group F₄. Since over the real numbers this is the only exceptional Jordan algebra, it is often referred to as "the" exceptional Jordan algebra. It was the first example of an Albert algebra
Albert algebra
In mathematics, an Albert algebra is a 27-dimensional exceptional Jordan algebra. They are named after Abraham Adrian Albert, who pioneered the study of non-associative algebras, usually working over the real numbers. Over the real numbers, there are two such Jordan algebras up to isomorphism...
.
Derivations and structure algebra
A derivationDerivation (abstract algebra)
In abstract algebra, a derivation is a function on an algebra which generalizes certain features of the derivative operator. Specifically, given an algebra A over a ring or a field K, a K-derivation is a K-linear map D: A → A that satisfies Leibniz's law: D = b + a.More...
of a Jordan algebra A is an endomorphism D of A such that D(xy) = D(x)y+xD(y). The derivations form a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
der(A). The Jordan identity implies that if x and y are elements of A, then the endomorphism sending z to x(yz)−y(xz) is a derivation. Thus the direct sum of A and der(A) can be made into a Lie algebra, called the structure algebra of A, str(A).
A simple example is provided by the Hermitian Jordan algebras H(A,σ). In this case any element x of A with σ(x)=−x defines a derivation. In many important examples, the structure algebra of H(A,σ) is A.
Derivation and structure algebras also form part of Tits' construction of the Freudenthal magic square
Freudenthal magic square
In mathematics, the Freudenthal magic square is a construction relating several Lie groups. It is named after Hans Freudenthal and Jacques Tits, who developed the idea independently. It associates a Lie group to a pair of division algebras A, B...
.
Formally real Jordan algebras
A (possibly nonassociative) algebra over the real numbers is said to be formally real if it satisfies the property that a sum of n squares can only vanish if each one vanishes individually. In 1932, Pascual Jordan attempted to axiomatize quantum theory by saying that the algebra of observables of any quantum system should be a formally real algebra which is commutative (xy = yx) and power-associative (the associative law holds for products involving only x, so that powers of any element x are unambiguously defined). He proved that any such algebra is a Jordan algebra.Not every Jordan algebra is formally real, but classified the finite dimensional formally real Jordan algebras. Every formally real Jordan algebra can be written as a direct sum of so-called simple ones, which are not themselves direct sums in a nontrivial way. In finite dimensions, the simple formally real Jordan algebras come in four infinite families, together with one exceptional case:
- The Jordan algebra of n×n self-adjoint real matrices, as above.
- The Jordan algebra of n×n self-adjoint complex matrices, as above.
- The Jordan algebra of n×n self-adjoint quaternionic matrices. as above.
- The Jordan algebra freely generated by Rn with the relations
- where the right-hand side is defined using the usual inner product on Rn. This is sometimes called a spin factor or a Jordan algebra of Clifford type.
- The Jordan algebra of 3×3 self-adjoint octonionic matrices, as above (an exceptional Jordan algebra called the Albert algebraAlbert algebraIn mathematics, an Albert algebra is a 27-dimensional exceptional Jordan algebra. They are named after Abraham Adrian Albert, who pioneered the study of non-associative algebras, usually working over the real numbers. Over the real numbers, there are two such Jordan algebras up to isomorphism...
).
- The Jordan algebra of 3×3 self-adjoint octonionic matrices, as above (an exceptional Jordan algebra called the Albert algebra
Of these possibilities, so far it appears that nature makes use only of the n×n complex matrices as algebras of observables. However, the spin factors play a role in special relativity, and all the formally real Jordan algebras are related to projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
.
Infinite dimensional Jordan algebras
In 1979, Efim ZelmanovEfim Zelmanov
Efim Isaakovich Zelmanov is a Russian mathematician, known for his work on combinatorial problems in nonassociative algebra and group theory, including his solution of the restricted Burnside problem. He was awarded a Fields Medal at the International Congress of Mathematicians in Zürich in...
classified infinite dimensional simple (and prime) Jordan algebras. They are either of Hermitian or Clifford type. In particular, the only exceptional simple (and prime) Jordan algebras are finite dimensional Albert algebra
Albert algebra
In mathematics, an Albert algebra is a 27-dimensional exceptional Jordan algebra. They are named after Abraham Adrian Albert, who pioneered the study of non-associative algebras, usually working over the real numbers. Over the real numbers, there are two such Jordan algebras up to isomorphism...
s, which have dimension 27.
Jordan rings
A Jordan ring is a generalization of Jordan algebras, requiring only that the Jordan ring be over a general ring rather than a field. Alternatively one can define a Jordan ring as a commutative nonassociative ringNonassociative ring
In abstract algebra, a nonassociative ring is a generalization of the concept of ring.A nonassociative ring is a set R with two operations, addition and multiplication, such that:# R is an abelian group under addition:## a+b = b+a...
that respects the Jordan identity.
Jordan superalgebras
The Jordan superalgebras over an algebraically closed field of characteristic 0 were classified by .They include several families and some exceptional algebras notably
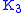and 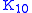Peirce decomposition
If e is an idempotent in a Jordan algebra A (e2=e) and R is the operation of multiplication by e, then- R(2R−1)(R−1) = 0
so the only eigenvalues of R are 0, 1/2, 1. If the Jordan algebra A is finite-dimensional over a field of characteristic not 2, this implies that it is a direct sum of subspaces A = A0(e) ⊕ A1/2(e) ⊕ A1(e) of the three eigenspaces. This decomposition was introduced by and is called the Peirce decomposition
Peirce decomposition
In algebra, a Peirce decomposition is a decomposition of an algebra as a sum of eigenspaces of commuting idempotents.The Peirce decomposition for associative algebras was introduced by...
of A relative to the idempotent e.