
Johnson bound
Encyclopedia
The Johnson bound is a bound on the size of error-correcting codes.
Let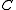 be a q-ary code
be a q-ary code
of length , i.e. a subset of
, i.e. a subset of  . Let
. Let  be the minimum distance of
be the minimum distance of 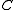 , i.e.
, i.e.
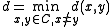
where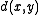 is the Hamming distance
is the Hamming distance
between and
and 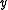 .
.
Let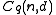 be the set of all q-ary codes with length
be the set of all q-ary codes with length  and minimum distance
and minimum distance  and let
and let 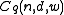 denote the set of codes in
denote the set of codes in  such that every element has exactly
such that every element has exactly 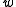 nonzero entries.
nonzero entries.
Denote by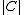 the number of elements in
the number of elements in  . Then, we define
. Then, we define 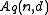 to be the largest size of a code with length
to be the largest size of a code with length  and minimum distance
and minimum distance  :
:
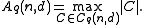
Similarly, we define to be the largest size of a code in
to be the largest size of a code in 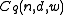 :
:
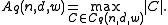
Theorem 1 (Johnson bound for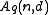 ):
):
If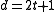 ,
,
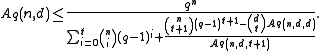
If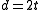 ,
,
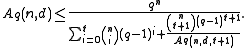
Theorem 2 (Johnson bound for ):
):
(i) If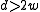 ,
,
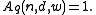
(ii) If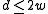 , then define the variable
, then define the variable  as follows. If
as follows. If 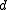 is even, then define
is even, then define  through the relation
through the relation 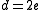 ; if
; if  is odd, define
is odd, define  through the relation
through the relation 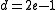 . Let
. Let 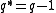 . Then,
. Then,
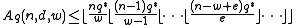
where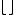 is the floor function
is the floor function
.
Remark: Plugging the bound of Theorem 2 into the bound of Theorem 1 produces a numerical upper bound on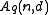 .
.
Let
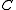 be a q-ary code
be a q-ary codeCode
A code is a rule for converting a piece of information into another form or representation , not necessarily of the same type....
of length
 , i.e. a subset of
, i.e. a subset of  . Let
. Let  be the minimum distance of
be the minimum distance of 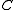 , i.e.
, i.e.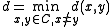
where
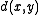 is the Hamming distance
is the Hamming distanceHamming distance
In information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different...
between
 and
and 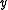 .
.Let
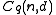 be the set of all q-ary codes with length
be the set of all q-ary codes with length  and minimum distance
and minimum distance  and let
and let 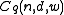 denote the set of codes in
denote the set of codes in  such that every element has exactly
such that every element has exactly 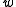 nonzero entries.
nonzero entries.Denote by
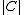 the number of elements in
the number of elements in  . Then, we define
. Then, we define 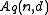 to be the largest size of a code with length
to be the largest size of a code with length  and minimum distance
and minimum distance  :
: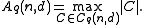
Similarly, we define
 to be the largest size of a code in
to be the largest size of a code in 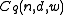 :
: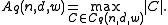
Theorem 1 (Johnson bound for
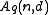 ):
):If
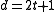 ,
,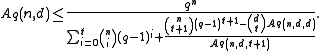
If
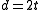 ,
,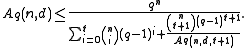
Theorem 2 (Johnson bound for
 ):
):(i) If
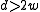 ,
,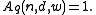
(ii) If
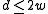 , then define the variable
, then define the variable  as follows. If
as follows. If 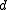 is even, then define
is even, then define  through the relation
through the relation 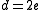 ; if
; if  is odd, define
is odd, define  through the relation
through the relation 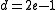 . Let
. Let 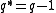 . Then,
. Then,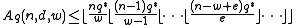
where
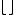 is the floor function
is the floor functionFloor function
In mathematics and computer science, the floor and ceiling functions map a real number to the largest previous or the smallest following integer, respectively...
.
Remark: Plugging the bound of Theorem 2 into the bound of Theorem 1 produces a numerical upper bound on
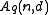 .
.See also
- Singleton boundSingleton boundIn coding theory, the Singleton bound, named after Richard Collom Singleton, is a relatively crude bound on the size of a block code C with block length n, size r and minimum distance d.-Statement of the Bound:...
- Hamming boundHamming boundIn mathematics and computer science, in the field of coding theory, the Hamming bound is a limit on the parameters of an arbitrary block code: it is also known as the sphere-packing bound or the volume bound from an interpretation in terms of packing balls in the Hamming metric into the space of...
- Plotkin boundPlotkin boundIn the mathematics of coding theory, the Plotkin bound, named after Morris Plotkin, is a bound on the maximum possible number of codewords in binary codes of given length n and given minimum distance d.- Statement of the bound :...
- Gilbert-Varshamov boundGilbert-Varshamov boundIn coding theory, the Gilbert–Varshamov bound is a bound on the parameters of a code . It is occasionally known as the Gilbert–Shannon–Varshamov bound , but the Gilbert–Varshamov bound is by far the most popular name...
- Griesmer boundGriesmer boundIn the mathematics of coding theory, the Griesmer bound, named after James Hugo Griesmer, is a bound on the length of binary codes of dimension k and minimum distance d.There is also a very similar version for non-binary codes....

