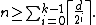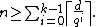Griesmer bound
Encyclopedia
In the mathematics
of coding theory
, the Griesmer bound, named after James Hugo Griesmer, is a bound on the length of binary code
s of dimension k and minimum distance d.
There is also a very similar version for non-binary codes.
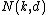 denote the minimum length of a binary code of dimension k and distance d. Let C be such a code.
denote the minimum length of a binary code of dimension k and distance d. Let C be such a code.
We want to show that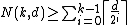 .
.
Let G be a generator matrix of C. We can always suppose that the first row of
G is of the form r = (1, ..., 1, 0, ..., 0) with weight d.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
of coding theory
Coding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
, the Griesmer bound, named after James Hugo Griesmer, is a bound on the length of binary code
Code
A code is a rule for converting a piece of information into another form or representation , not necessarily of the same type....
s of dimension k and minimum distance d.
There is also a very similar version for non-binary codes.
Statement of the bound
For a binary linear code, the Griesmer bound says:Proof
Let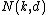 denote the minimum length of a binary code of dimension k and distance d. Let C be such a code.
denote the minimum length of a binary code of dimension k and distance d. Let C be such a code.We want to show that
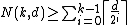 .
.Let G be a generator matrix of C. We can always suppose that the first row of
G is of the form r = (1, ..., 1, 0, ..., 0) with weight d.
-
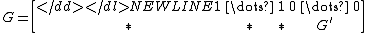
The matrix G' generates a code C', which is called the residual code of C.
C' has obviously dimension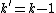 and length
and length 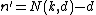 .
.
C' has a distance d', but we don't know it.
Let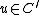 s.t.
s.t. 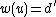 . There exists a vector
. There exists a vector
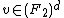 s.t. the concatenation
s.t. the concatenation 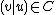 .
.
Then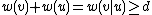 . On the other hand, also
. On the other hand, also 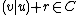 , since
, since 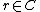 and
and 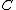 is linear, so
is linear, so 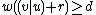 . But
. But
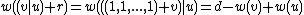 ,
,
so this becomes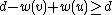 . By summing this with
. By summing this with 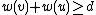 , we obtain
, we obtain 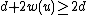 . But
. But 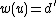 , so we get
, so we get
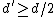 . This implies
. This implies 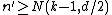 , therefore
, therefore 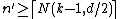 (due to the integrality of n'), so that
(due to the integrality of n'), so that
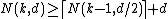 .
.
By induction over k we will eventually get
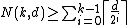
(note that at any step the dimension decreases by 1 and the distance is halved, and we use the identity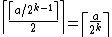 for any integer a and positive integer k).
for any integer a and positive integer k).
The bound for the general case
For a linear code over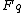 , the Griesmer bound becomes:
, the Griesmer bound becomes:
The proof is similar to the binary case and so it is omitted.
See also
- Singleton boundSingleton boundIn coding theory, the Singleton bound, named after Richard Collom Singleton, is a relatively crude bound on the size of a block code C with block length n, size r and minimum distance d.-Statement of the Bound:...
- Hamming boundHamming boundIn mathematics and computer science, in the field of coding theory, the Hamming bound is a limit on the parameters of an arbitrary block code: it is also known as the sphere-packing bound or the volume bound from an interpretation in terms of packing balls in the Hamming metric into the space of...
- Gilbert-Varshamov boundGilbert-Varshamov boundIn coding theory, the Gilbert–Varshamov bound is a bound on the parameters of a code . It is occasionally known as the Gilbert–Shannon–Varshamov bound , but the Gilbert–Varshamov bound is by far the most popular name...
- Johnson bound
- Plotkin boundPlotkin boundIn the mathematics of coding theory, the Plotkin bound, named after Morris Plotkin, is a bound on the maximum possible number of codewords in binary codes of given length n and given minimum distance d.- Statement of the bound :...
-