Jenkins-Traub algorithm
Encyclopedia
The Jenkins–Traub algorithm for polynomial zeros is a fast globally convergent iterative method published in 1970 by Michael A. Jenkins and Joseph F. Traub. It is "practically a standard in black-box polynomial root-finders".
Given a polynomial P,
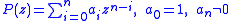
with complex coefficients compute approximations to the n zeros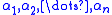
of P(z).
There is a variation of the Jenkins–Traub algorithm which is faster if the coefficients are real. The Jenkins–Traub algorithm has stimulated considerable research on theory and software for methods of this type.
with complex coefficients. The algorithm starts by checking the polynomial for the occurrence of very large or very small roots. If necessary, the coefficients are rescaled by a rescaling of the variable. In the algorithm proper, roots are found one by one and generally in increasing size. After each root is found, the polynomial is deflated by dividing off the corresponding linear factor. Indeed, the factorization of the polynomial into the linear factor and the remaining deflated polynomial is already a result of the root-finding procedure. The root-finding procedure has three stages that correspond to different variants of the inverse power iteration. See Jenkins and Traub
.
A description can also be found in Ralston and
Rabinowitz
p. 383.
The algorithm is similar in spirit to the two-stage algorithm studied by Traub.
polynomials that keeps the coefficients in a numerically sensible range.
The construction of the H polynomials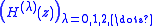
depends on a sequence of complex numbers 
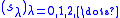called shifts. These shifts themselves depend, at least in the third stage, on the previous H polynomials. The H polynomials are defined as the solution to the implicit recursion
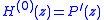and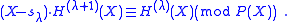 
A direct solution to this implicit equation is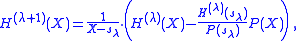
where the polynomial division is exact.
Algorithmically, one would use for instance the Horner scheme
or Ruffini rule to evaluate the polynomials at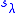
and obtain the quotients at the same time. With the resulting quotients p(X) and h(X) as intermediate results the next H polynomial is obtained as
Since the highest degree coefficient is obtained from P(X), the leading coefficient of
is 
. If this is divided out the normalized H polynomial is
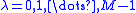set 
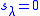. Usually M=5 is chosen for polynomials of moderate degrees up to n = 50. This stage is not necessary from theoretical considerations alone, but is useful in practice. It emphasizes in the H polynomials the cofactor (of the linear factor) of the smallest root.
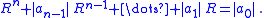
Since the left side is a convex function and increases monotonically from zero to infinity, this equation is easy to solve, for instance by Newton's method
.
Now choose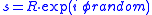
on the circle of this radius. The sequence of polynomials 
, 
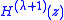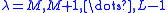, is generated with the fixed shift value 
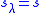. During this iteration, the current approximation for the root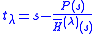
is traced. The second stage is finished successfully if the conditions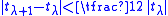
and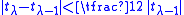 
are simultaneously met. If there was no success after some number of iterations, a different random point on the circle is tried. Typically one uses a number of 9 iterations for polynomials of moderate degree, with a doubling strategy for the case of multiple failures.
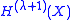are now generated using the variable shifts 
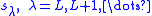which are generated by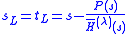
being the last root estimate of the second stage and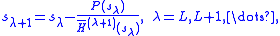
If the step size in stage three does not fall fast enough to zero, then stage two is restarted using a different random point. If this does not succeed after a small number of restarts, the number of steps in stage two is doubled.
The algorithm converges for any distribution of roots, but may fail to find all roots of the polynomial. Furthermore, the convergence is slightly faster than the quadratic convergence
of Newton–Raphson iteration, however, it uses at least twice as many operations per step.
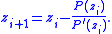
The iteration uses the given P and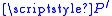
. In contrast the third-stage of Jenkins–Traub
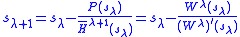
is precisely a Newton–Raphson iteration performed on certain rational functions. More precisely, Newton–Raphson is being performed on a sequence of rational functions
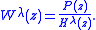
For
sufficiently large,
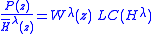
is as close as desired to a first degree polynomial
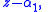
where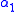
is one of the zeros of 
. Even though Stage 3 is precisely a Newton–Raphson iteration, differentiation is not performed.
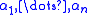be the roots of P(X). The so called Lagrange factors of P(X) are the cofactors of these roots,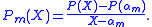
If all roots are different, then the Lagrange factors form a basis of the space of polynomials of degree at most n − 1. By analysis of the recursion procedure one finds that the H polynomials have the coordinate representation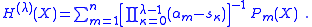
Each Lagrange factor has leading coefficient 1, so that the leading coefficient of the H polynomials is the sum of the coefficients. The normalized H polynomials are thus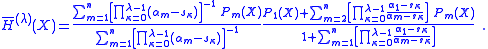
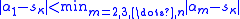holds for almost all iterates, the normalized H polynomials will converge at least geometrically towards 
.
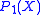Under the condition that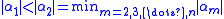
one gets the aymptotic estimates for
Given a polynomial P,
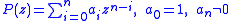
with complex coefficients compute approximations to the n zeros
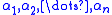of P(z).There is a variation of the Jenkins–Traub algorithm which is faster if the coefficients are real. The Jenkins–Traub algorithm has stimulated considerable research on theory and software for methods of this type.
Overview
The Jenkins–Traub algorithm calculates all of the roots of a polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
with complex coefficients. The algorithm starts by checking the polynomial for the occurrence of very large or very small roots. If necessary, the coefficients are rescaled by a rescaling of the variable. In the algorithm proper, roots are found one by one and generally in increasing size. After each root is found, the polynomial is deflated by dividing off the corresponding linear factor. Indeed, the factorization of the polynomial into the linear factor and the remaining deflated polynomial is already a result of the root-finding procedure. The root-finding procedure has three stages that correspond to different variants of the inverse power iteration. See Jenkins and Traub
Joseph F Traub
Joseph Frederick Traub , is a computer scientist. He is the Edwin Howard Armstrong Professor of Computer Science at Columbia University and External Professor at the Santa Fe Institute...
.
A description can also be found in Ralston and
Rabinowitz
Philip Rabinowitz (mathematician)
Philip Rabinowitz was an American and Israeli applied mathematician. He was best known for his work in numerical analysis, including his books A First Course in Numerical Analysis with Anthony Ralston and Methods of Numerical Integration with Philip J. Davis...
p. 383.
The algorithm is similar in spirit to the two-stage algorithm studied by Traub.
Root-finding procedure
Starting with the current polynomial P(X) of degree n, the smallest root of P(x) is computed. To that end, a sequence of so called H polynomials is constructed. These polynomials are all of degree n − 1 and are supposed to converge to the factor of P(X) containing all the remaining roots. The sequence of H polynomials occurs in two variants, an unnormalized variant that allows easy theoretical insights and a normalized variant of polynomials that keeps the coefficients in a numerically sensible range.The construction of the H polynomials
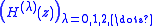depends on a sequence of complex numbers 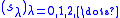called shifts. These shifts themselves depend, at least in the third stage, on the previous H polynomials. The H polynomials are defined as the solution to the implicit recursion 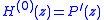and 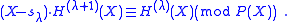A direct solution to this implicit equation is
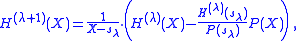
where the polynomial division is exact.
Algorithmically, one would use for instance the Horner scheme
Horner scheme
In numerical analysis, the Horner scheme , named after William George Horner, is an algorithm for the efficient evaluation of polynomials in monomial form. Horner's method describes a manual process by which one may approximate the roots of a polynomial equation...
or Ruffini rule to evaluate the polynomials at
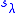and obtain the quotients at the same time. With the resulting quotients p(X) and h(X) as intermediate results the next H polynomial is obtained asSince the highest degree coefficient is obtained from P(X), the leading coefficient of
is . If this is divided out the normalized H polynomial isStage one: no-shift process
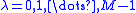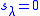For set . Usually M=5 is chosen for polynomials of moderate degrees up to n = 50. This stage is not necessary from theoretical considerations alone, but is useful in practice. It emphasizes in the H polynomials the cofactor (of the linear factor) of the smallest root.Stage two: fixed-shift process
The shift for this stage is determined as some point close to the smallest root of the polynomial. It is quasi-randomly located on the circle with the inner root radius, which in turn is estimated as the positive solution of the equation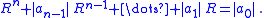Since the left side is a convex function and increases monotonically from zero to infinity, this equation is easy to solve, for instance by Newton's method
Newton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
.
Now choose
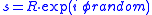on the circle of this radius. The sequence of polynomials 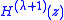, , 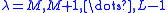is generated with the fixed shift value 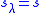. During this iteration, the current approximation for the root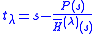is traced. The second stage is finished successfully if the conditions
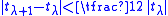and 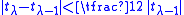are simultaneously met. If there was no success after some number of iterations, a different random point on the circle is tried. Typically one uses a number of 9 iterations for polynomials of moderate degree, with a doubling strategy for the case of multiple failures.
Stage three: variable-shift process
The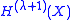 are now generated using the variable shifts 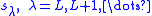which are generated bybeing the last root estimate of the second stage and
- where
is the normalized H polynomial, that is 
divided by its leading coefficient.
If the step size in stage three does not fall fast enough to zero, then stage two is restarted using a different random point. If this does not succeed after a small number of restarts, the number of steps in stage two is doubled.
Convergence
It can be shown that, provided L is chosen sufficiently large, sλ always converges to a root of P.The algorithm converges for any distribution of roots, but may fail to find all roots of the polynomial. Furthermore, the convergence is slightly faster than the quadratic convergence
Rate of convergence
In numerical analysis, the speed at which a convergent sequence approaches its limit is called the rate of convergence. Although strictly speaking, a limit does not give information about any finite first part of the sequence, this concept is of practical importance if we deal with a sequence of...
of Newton–Raphson iteration, however, it uses at least twice as many operations per step.
What gives the algorithm its power?
Compare with the Newton–Raphson iteration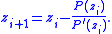The iteration uses the given P and
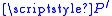. In contrast the third-stage of Jenkins–Traub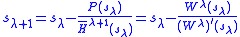is precisely a Newton–Raphson iteration performed on certain rational functions. More precisely, Newton–Raphson is being performed on a sequence of rational functions
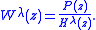
For
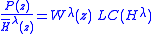
sufficiently large,is as close as desired to a first degree polynomial
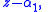
where
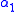is one of the zeros of . Even though Stage 3 is precisely a Newton–Raphson iteration, differentiation is not performed.Analysis of the H polynomials
Let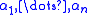 be the roots of P(X). The so called Lagrange factors of P(X) are the cofactors of these roots,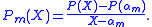If all roots are different, then the Lagrange factors form a basis of the space of polynomials of degree at most n − 1. By analysis of the recursion procedure one finds that the H polynomials have the coordinate representation
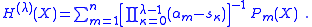
Each Lagrange factor has leading coefficient 1, so that the leading coefficient of the H polynomials is the sum of the coefficients. The normalized H polynomials are thus
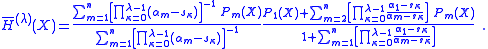
Convergence orders
If the condition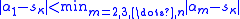 holds for almost all iterates, the normalized H polynomials will converge at least geometrically towards 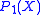.Under the condition that
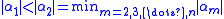
one gets the aymptotic estimates for
- stage 1:
- for stage 2, if s is close enough to
:
-
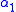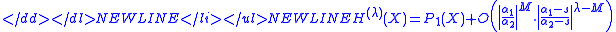
- and
- and for stage 3:
-
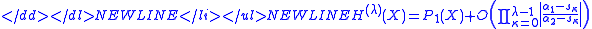
- and
- giving rise to a higher than quadratic convergence order of
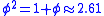, where 
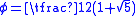is the golden ratioGolden ratioIn mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
.
Interpretation as inverse power iteration
All stages of the Jenkins–Traub complex algorithm may be represented as the linear algebra problem of determining the eigenvalues of a special matrix. This matrix is the coordinate representation of a linear map in the n-dimensional space of polynomials of degree n − 1 or less. The principal idea of this map is to interpret the factorization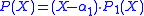
with a root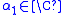
and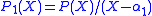 
the remaining factor of degree n − 1 as the eigenvector equation for the multiplication with the variable X, followed by remainder computation with divisor P(X),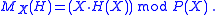
This maps polynomials of degree at most n − 1 to polynomials of degree at most n − 1. The eigenvalues of this map are the roots of P(X), since the eigenvector equation reads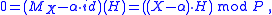
which implies that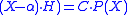
, that is, 
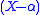is a linear factor of P(X). In the monomial basis the linear map 
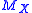is represented by a companion matrix of the polynomial P, as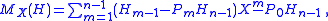
the resulting coefficient matrix is
To this matrix the inverse power iteration is applied in the three variants of no shift, constant shift and generalized Rayleigh shift in the three stages of the algorithm. It is more efficient to perform the linear algebra operations in polynomial arithmetic and not by matrix operations, however, the properties of the inverse power iteration remain the same.
Real coefficients
The Jenkins–Traub algorithm described earlier works for polynomials with complex coefficients. The same authors also created a three-stage algorithm for polynomials with real coefficients. See Jenkins and Traub A Three-Stage Algorithm for Real Polynomials Using Quadratic Iteration. The algorithm finds either a linear or quadratic factor working completely in real arithmetic. If the complex and real algorithms are applied to the same real polynomial, the real algorithm is about four times as fast. The real algorithm always converges and the rate of convergence is greater than second order.
A connection with the shifted QR algorithm
There is a surprising connection with the shifted QR algorithm for computing matrix eigenvalues. See Dekker and Traub The shifted QR algorithm for Hermitian matrices. Again the shifts may be viewed as Newton-Raphson iteration on a sequence of rational functions converging to a first degree polynomial.
Software and testing
The software for the Jenkins–Traub algorithm was published as Jenkins and Traub Algorithm 419: Zeros of a Complex Polynomial. The software for the real algorithm was published as Jenkins Algorithm 493: Zeros of a Real Polynomial.
The methods have been extensively tested by many people. As predicted they enjoy faster than quadratic convergence for all distributions of zeros.
However there are polynomials which can cause loss of precision as illustrated by the following example. The polynomial has all its zeros lying on two half-circles of different radii. WilkinsonJames H. WilkinsonJames Hardy Wilkinson was a prominent figure in the field of numerical analysis, a field at the boundary of applied mathematics and computer science particularly useful to physics and engineering.-Early life:...
recommends that it is desirable for stable deflation that smaller zeros be computed first. The second-stage shifts are chosen so that the zeros on the smaller half circle are found first. After deflation the polynomial with the zeros on the half circle is known to be ill-conditioned if the degree is large; see Wilkinson, p. 64. The original polynomial was of degree 60 and suffered severe deflation instability.
External links
- Additional Bibliography for the Jenkins–Traub Method
- Internet Resources for the Jenkins–Traub Method
- A free downloadable Windows application using the Jenkins–Traub Method for polynomials with real and complex coefficients
- CPOLY (Algorithm 419 from Comm. ACM) on NetlibNetlibNetlib is a repository of software for scientific computing maintained by AT&T, Bell Laboratories, the University of Tennessee and Oak Ridge National Laboratory. Netlib comprises a large number of separate programs and libraries...
. In FortranFortranFortran is a general-purpose, procedural, imperative programming language that is especially suited to numeric computation and scientific computing...
. - RPOLY Algorithm 493 from ACM TOMS) on Netlib. In Fortran.
- Online Calculator Online Polynomial Calculator using the Jenkins Traub procedure
- giving rise to a higher than quadratic convergence order of
-
- and for stage 3:
-
- for stage 2, if s is close enough to