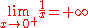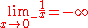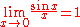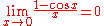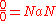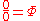James Anderson (computer scientist)
Encyclopedia
James Anderson is an academic staff member in the School of Systems Engineering at the University of Reading
, England
. He is currently teaching compilers, algorithms, and computer algebra, and in the past he has taught programming and computer graphics
.
Anderson quickly gained publicity in December 2006 in the United Kingdom
when the regional BBC South Today reported his claim of "having solved a 1200 year old problem", namely that of division by zero
. However, commentators quickly pointed out that his ideas are just a variation of the standard IEEE 754 concept of NaN
(Not a Number), a datum that has been commonly employed on computer
s in floating point
arithmetic
for many years. Dr Anderson defended the criticism of his claims on BBC Berkshire on 12 December 2006, saying, "If anyone doubts me I can hit them over the head with a computer that does it."
, the British Machine Vision Association, Eurographics
, and the British Society for the Philosophy of Science. He is also a teacher in the Computer Science department (School of Systems Engineering) at the University of Reading
. He was
a psychology graduate who worked in the Electrical and Electronic Engineering departments at the University of Sussex
and Plymouth Polytechnic (now the University of Plymouth
). His doctorate is from the University of Reading for (in Anderson's words) "developing a canonical description of the perspective transformations in whole numbered dimensions".
He has written two papers on division by zero
and has invented what he calls the "Perspex machine".
Anderson claims that "mathematical arithmetic is sociologically invalid" and that IEEE floating-point arithmetic, with NaN, is also faulty.
Anderson's transreal numbers were first mentioned in a 1997 publication, and made well-known on the Internet
in 2006, but not accepted as useful by the mathematics community. These numbers are used in his concept of transreal arithmetic and the Perspex machine. According to Anderson, transreal numbers include all of the real number
s, plus three others: infinity
( ), negative infinity (
), negative infinity ( ) and "nullity" (
) and "nullity" (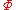 ), a numerical representation of a non-number that lies outside of the affinely extended real number line. (Nullity
), a numerical representation of a non-number that lies outside of the affinely extended real number line. (Nullity
, confusingly, has an existing mathematical meaning.)
Anderson intends the axiom
s of transreal arithmetic to complement the axioms of standard arithmetic; they are supposed to produce the same result as standard arithmetic for all calculations where standard arithmetic defines a result. In addition, they are intended to define a consistent numeric result for the calculations which are undefined in standard arithmetic, such as division by zero
.
. The reason for this is simple: A statement about the quotient of two numbers is understood in mathematics as another statement about multiplcation. Specifically, if
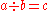
this is understood as simply another way of saying that
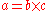
Thus, if for some number
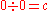
then this is just another way of saying that

But in fact this is true for all real numbers . And that is precisely the reason that mathematicians do not assign a single value to
. And that is precisely the reason that mathematicians do not assign a single value to  but rather label it "indeterminate". Assigning a value to
but rather label it "indeterminate". Assigning a value to  , even a newly fabricated "number", misses the point entirely.
, even a newly fabricated "number", misses the point entirely.
In computer arithmetic, the symbol is not meant to be a number, but rather an error message conveying the fact that the arithmetical operation the computer just attempted cannot be assigned a single number as an answer—even if
is not meant to be a number, but rather an error message conveying the fact that the arithmetical operation the computer just attempted cannot be assigned a single number as an answer—even if  and
and  are considered numbers.
are considered numbers.
Because is an error message and not a number, there is no reason to assign
is an error message and not a number, there is no reason to assign  to the comparison
to the comparison  .
.
By contrast, so-called "transreal arithmetic" resembles IEEE floating point arithmetic, a floating point
arithmetic commonly used on computer
s. In IEEE floating point arithmetic, calculations such as zero divided by zero can produce a result, Not a Number (NaN)
, to which the standard arithmetic axioms do not apply (as it is not a number). IEEE floating point arithmetic, like transreal arithmetic, uses affine infinity (two separate infinities, one positive and one negative) rather than projective infinity (a single unsigned infinity, turning the number line into a loop). The IEEE standard extends standard arithmetic by defining the results of all arithmetic operations upon ,
,  , and NaN.
, and NaN.
Loosely put, IEEE floating point arithmetic extends the (affinely) extended real number line to the set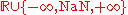 and transreal arithmetic extends the (affinely) extended real number line to the set
and transreal arithmetic extends the (affinely) extended real number line to the set 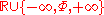 . IEEE floating point arithmetic approximates this set, defining a finite binary representation, for actual use in computers, that includes denormal number
. IEEE floating point arithmetic approximates this set, defining a finite binary representation, for actual use in computers, that includes denormal number
s and negative zero. Transreal arithmetic has no standardized binary encoding for use in computers.
Just as in IEEE floating point arithemetic, in transreal arithmetic, all calculations including infinity and nullity are axiom
atically defined. In addition, several of the axioms of standard arithmetic are constrained so that they do not operate upon the extended members of the number set. Here are some identities
in transreal arithmetic with the IEEE equivalents:
The main difference between transreal arithmetic and IEEE floating-point arithmetic is that whilst nullity compares equal to nullity, NaN does not compare equal to NaN.
Anderson's analysis of the properties of transreal algebra is given in his paper on "perspex machines".
Due to the more expansive definition of numbers in transreal arithmetic, several identities and theorems which apply to all numbers in standard arithmetic are not universal in transreal arithmetic. For instance, in transreal arithmetic, is not true for all
is not true for all  , since
, since  . That problem is addressed in ref. pg. 7. Similarly, it is not always the case in transreal arithmetic that a number can be cancelled with its reciprocal
. That problem is addressed in ref. pg. 7. Similarly, it is not always the case in transreal arithmetic that a number can be cancelled with its reciprocal
to yield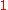 . Cancelling zero with its reciprocal in fact yields nullity.
. Cancelling zero with its reciprocal in fact yields nullity.
Examining the axiom
s provided by Anderson, it is easy to see that any term which contains an occurrence of the constant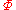 is provably equivalent to
is provably equivalent to 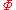 . Formally, let
. Formally, let  be any term with a sub-term
be any term with a sub-term 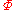 , then
, then
 is a theorem
is a theorem
of the theory proposed by Anderson.
with its report in December 2006 where Anderson was featured on a BBC television segment teaching schoolchildren about his concept of "nullity". The report implied that Anderson had discovered the solution to division by zero, rather than simply attempting to formalize it. The report also suggested that Anderson was the first to solve this problem, when in fact the result of zero divided by zero has been expressed formally in a number of different ways (for example, NaN
).
The BBC was criticized for irresponsible journalism, but the producers of the segment defended the BBC, stating that the report was a light-hearted look at a mathematical problem aimed at a mainstream, regional audience for BBC South Today rather than at a global audience of mathematicians. The BBC later posted a follow-up giving Anderson's response to many claims that the theory is flawed.
University of Reading
The University of Reading is a university in the English town of Reading, Berkshire. The University was established in 1892 as University College, Reading and received its Royal Charter in 1926. It is based on several campuses in, and around, the town of Reading.The University has a long tradition...
, England
England
England is a country that is part of the United Kingdom. It shares land borders with Scotland to the north and Wales to the west; the Irish Sea is to the north west, the Celtic Sea to the south west, with the North Sea to the east and the English Channel to the south separating it from continental...
. He is currently teaching compilers, algorithms, and computer algebra, and in the past he has taught programming and computer graphics
Computer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
.
Anderson quickly gained publicity in December 2006 in the United Kingdom
United Kingdom
The United Kingdom of Great Britain and Northern IrelandIn the United Kingdom and Dependencies, other languages have been officially recognised as legitimate autochthonous languages under the European Charter for Regional or Minority Languages...
when the regional BBC South Today reported his claim of "having solved a 1200 year old problem", namely that of division by zero
Division by zero
In mathematics, division by zero is division where the divisor is zero. Such a division can be formally expressed as a / 0 where a is the dividend . Whether this expression can be assigned a well-defined value depends upon the mathematical setting...
. However, commentators quickly pointed out that his ideas are just a variation of the standard IEEE 754 concept of NaN
NaN
In computing, NaN is a value of the numeric data type representing an undefined or unrepresentable value, especially in floating-point calculations...
(Not a Number), a datum that has been commonly employed on computer
Computer
A computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...
s in floating point
Floating point
In computing, floating point describes a method of representing real numbers in a way that can support a wide range of values. Numbers are, in general, represented approximately to a fixed number of significant digits and scaled using an exponent. The base for the scaling is normally 2, 10 or 16...
arithmetic
Arithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
for many years. Dr Anderson defended the criticism of his claims on BBC Berkshire on 12 December 2006, saying, "If anyone doubts me I can hit them over the head with a computer that does it."
Research and background
Mr Anderson is a member of the British Computer SocietyBritish Computer Society
The British Computer Society, is a professional body and a learned society that represents those working in Information Technology in the United Kingdom and internationally...
, the British Machine Vision Association, Eurographics
Eurographics
Eurographics is a Europe-wide professional Computer Graphics association. The association supports its members in advancing the state of the art in Computer Graphics and related fields such as Multimedia, Scientific Visualization and Human-Computer Interaction....
, and the British Society for the Philosophy of Science. He is also a teacher in the Computer Science department (School of Systems Engineering) at the University of Reading
University of Reading
The University of Reading is a university in the English town of Reading, Berkshire. The University was established in 1892 as University College, Reading and received its Royal Charter in 1926. It is based on several campuses in, and around, the town of Reading.The University has a long tradition...
. He was
a psychology graduate who worked in the Electrical and Electronic Engineering departments at the University of Sussex
University of Sussex
The University of Sussex is an English public research university situated next to the East Sussex village of Falmer, within the city of Brighton and Hove. The University received its Royal Charter in August 1961....
and Plymouth Polytechnic (now the University of Plymouth
University of Plymouth
Plymouth University is the largest university in the South West of England, with over 30,000 students and is 9th largest in the United Kingdom by total number of students . It has almost 3,000 staff...
). His doctorate is from the University of Reading for (in Anderson's words) "developing a canonical description of the perspective transformations in whole numbered dimensions".
He has written two papers on division by zero
Division by zero
In mathematics, division by zero is division where the divisor is zero. Such a division can be formally expressed as a / 0 where a is the dividend . Whether this expression can be assigned a well-defined value depends upon the mathematical setting...
and has invented what he calls the "Perspex machine".
Anderson claims that "mathematical arithmetic is sociologically invalid" and that IEEE floating-point arithmetic, with NaN, is also faulty.
Transreal arithmetic
In mathematical analysis, the following limits can be found: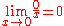
 is also an indeterminate form is also an indeterminate formIndeterminate form In calculus and other branches of mathematical analysis, an indeterminate form is an algebraic expression obtained in the context of limits. Limits involving algebraic operations are often performed by replacing subexpressions by their limits; if the expression obtained after this substitution... . See exponentiation. |
In IEEE floating-point arithmetic:
In several computer programming languages, including C C (programming language) C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system.... 's pow function,  is defined to be is defined to be 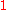 , as that is the most convenient value for numerical analysis programs, since it makes , as that is the most convenient value for numerical analysis programs, since it makes 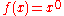 (and many other functions) continuous (and many other functions) continuousContinuous function In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of... at zero, with the notable exception of 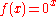 . . |
In transreal arithmetic:
|
Anderson's transreal numbers were first mentioned in a 1997 publication, and made well-known on the Internet
Internet
The Internet is a global system of interconnected computer networks that use the standard Internet protocol suite to serve billions of users worldwide...
in 2006, but not accepted as useful by the mathematics community. These numbers are used in his concept of transreal arithmetic and the Perspex machine. According to Anderson, transreal numbers include all of the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, plus three others: infinity
Infinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
(
 ), negative infinity (
), negative infinity ( ) and "nullity" (
) and "nullity" (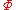 ), a numerical representation of a non-number that lies outside of the affinely extended real number line. (Nullity
), a numerical representation of a non-number that lies outside of the affinely extended real number line. (NullityNullity
Nullity may refer to:* Nullity , a legal declaration that no marriage had ever come into being* Nullity, the dimension of the null space of a mathematical operator or matrix...
, confusingly, has an existing mathematical meaning.)
Anderson intends the axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s of transreal arithmetic to complement the axioms of standard arithmetic; they are supposed to produce the same result as standard arithmetic for all calculations where standard arithmetic defines a result. In addition, they are intended to define a consistent numeric result for the calculations which are undefined in standard arithmetic, such as division by zero
Division by zero
In mathematics, division by zero is division where the divisor is zero. Such a division can be formally expressed as a / 0 where a is the dividend . Whether this expression can be assigned a well-defined value depends upon the mathematical setting...
.
Transreal arithmetic and other arithmetics
In standard arithmetic, division of zero by zero is considered indeterminateIndeterminate form
In calculus and other branches of mathematical analysis, an indeterminate form is an algebraic expression obtained in the context of limits. Limits involving algebraic operations are often performed by replacing subexpressions by their limits; if the expression obtained after this substitution...
. The reason for this is simple: A statement about the quotient of two numbers is understood in mathematics as another statement about multiplcation. Specifically, if
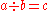
this is understood as simply another way of saying that
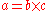
Thus, if for some number

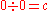
then this is just another way of saying that

But in fact this is true for all real numbers
 . And that is precisely the reason that mathematicians do not assign a single value to
. And that is precisely the reason that mathematicians do not assign a single value to  but rather label it "indeterminate". Assigning a value to
but rather label it "indeterminate". Assigning a value to  , even a newly fabricated "number", misses the point entirely.
, even a newly fabricated "number", misses the point entirely.In computer arithmetic, the symbol
 is not meant to be a number, but rather an error message conveying the fact that the arithmetical operation the computer just attempted cannot be assigned a single number as an answer—even if
is not meant to be a number, but rather an error message conveying the fact that the arithmetical operation the computer just attempted cannot be assigned a single number as an answer—even if  and
and  are considered numbers.
are considered numbers.Because
 is an error message and not a number, there is no reason to assign
is an error message and not a number, there is no reason to assign 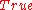 to the comparison
to the comparison  .
.By contrast, so-called "transreal arithmetic" resembles IEEE floating point arithmetic, a floating point
Floating point
In computing, floating point describes a method of representing real numbers in a way that can support a wide range of values. Numbers are, in general, represented approximately to a fixed number of significant digits and scaled using an exponent. The base for the scaling is normally 2, 10 or 16...
arithmetic commonly used on computer
Computer
A computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...
s. In IEEE floating point arithmetic, calculations such as zero divided by zero can produce a result, Not a Number (NaN)
NaN
In computing, NaN is a value of the numeric data type representing an undefined or unrepresentable value, especially in floating-point calculations...
, to which the standard arithmetic axioms do not apply (as it is not a number). IEEE floating point arithmetic, like transreal arithmetic, uses affine infinity (two separate infinities, one positive and one negative) rather than projective infinity (a single unsigned infinity, turning the number line into a loop). The IEEE standard extends standard arithmetic by defining the results of all arithmetic operations upon
 ,
,  , and NaN.
, and NaN.Loosely put, IEEE floating point arithmetic extends the (affinely) extended real number line to the set
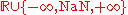 and transreal arithmetic extends the (affinely) extended real number line to the set
and transreal arithmetic extends the (affinely) extended real number line to the set 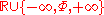 . IEEE floating point arithmetic approximates this set, defining a finite binary representation, for actual use in computers, that includes denormal number
. IEEE floating point arithmetic approximates this set, defining a finite binary representation, for actual use in computers, that includes denormal numberDenormal number
In computer science, denormal numbers or denormalized numbers fill the underflow gap around zero in floating point arithmetic: any non-zero number which is smaller than the smallest normal number is 'sub-normal'.For example, if the smallest positive 'normal' number is 1×β−n In computer...
s and negative zero. Transreal arithmetic has no standardized binary encoding for use in computers.
Just as in IEEE floating point arithemetic, in transreal arithmetic, all calculations including infinity and nullity are axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
atically defined. In addition, several of the axioms of standard arithmetic are constrained so that they do not operate upon the extended members of the number set. Here are some identities
Identity (mathematics)
In mathematics, the term identity has several different important meanings:*An identity is a relation which is tautologically true. This means that whatever the number or value may be, the answer stays the same. For example, algebraically, this occurs if an equation is satisfied for all values of...
in transreal arithmetic with the IEEE equivalents:
| Transreal arithmetic | IEEE standard floating point arithmetic |
|---|---|
|
|
  |
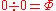 |
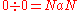 |
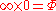 |
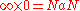 |
 |
 |
 |
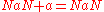 |
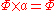 |
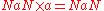 |
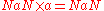 |
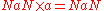 (i.e. applying unary negation to NaN yields NaN) (i.e. applying unary negation to NaN yields NaN) |
 |
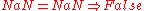 |
The main difference between transreal arithmetic and IEEE floating-point arithmetic is that whilst nullity compares equal to nullity, NaN does not compare equal to NaN.
Anderson's analysis of the properties of transreal algebra is given in his paper on "perspex machines".
Due to the more expansive definition of numbers in transreal arithmetic, several identities and theorems which apply to all numbers in standard arithmetic are not universal in transreal arithmetic. For instance, in transreal arithmetic,
 is not true for all
is not true for all  , since
, since  . That problem is addressed in ref. pg. 7. Similarly, it is not always the case in transreal arithmetic that a number can be cancelled with its reciprocal
. That problem is addressed in ref. pg. 7. Similarly, it is not always the case in transreal arithmetic that a number can be cancelled with its reciprocalMultiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
to yield
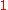 . Cancelling zero with its reciprocal in fact yields nullity.
. Cancelling zero with its reciprocal in fact yields nullity.Examining the axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s provided by Anderson, it is easy to see that any term which contains an occurrence of the constant
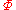 is provably equivalent to
is provably equivalent to 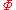 . Formally, let
. Formally, let  be any term with a sub-term
be any term with a sub-term 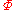 , then
, then is a theorem
is a theoremTheorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
of the theory proposed by Anderson.
Media coverage
Anderson's transreal arithmetic, and concept of "nullity" in particular, were introduced to the public by the BBCBBC
The British Broadcasting Corporation is a British public service broadcaster. Its headquarters is at Broadcasting House in the City of Westminster, London. It is the largest broadcaster in the world, with about 23,000 staff...
with its report in December 2006 where Anderson was featured on a BBC television segment teaching schoolchildren about his concept of "nullity". The report implied that Anderson had discovered the solution to division by zero, rather than simply attempting to formalize it. The report also suggested that Anderson was the first to solve this problem, when in fact the result of zero divided by zero has been expressed formally in a number of different ways (for example, NaN
NaN
In computing, NaN is a value of the numeric data type representing an undefined or unrepresentable value, especially in floating-point calculations...
).
The BBC was criticized for irresponsible journalism, but the producers of the segment defended the BBC, stating that the report was a light-hearted look at a mathematical problem aimed at a mainstream, regional audience for BBC South Today rather than at a global audience of mathematicians. The BBC later posted a follow-up giving Anderson's response to many claims that the theory is flawed.