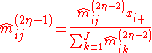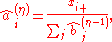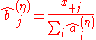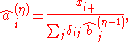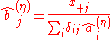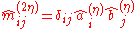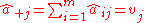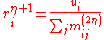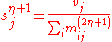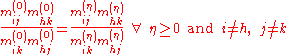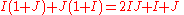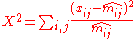Iterative proportional fitting
Encyclopedia
The iterative proportional fitting procedure (IPFP, also known as biproportional fitting in statistics, RAS algorithm in economics and matrix raking or matrix scaling in computer science) is an iterative algorithm for estimating cell values of a contingency table
such that the marginal totals remain fixed and the estimated table decomposes into an outer product
.
First introduced by Deming
and Stephan in 1940 (they proposed IPFP as an algorithm leading to a minimizer of the Pearson X-squared statistic, which it does not, and even failed to prove convergence), it has seen various extensions and related research. A rigorous proof of convergence by means of differential geometry is due to Fienberg
(1970). He interpreted the family of contingency tables of constant crossproduct ratios as a particular (IJ − 1)-dimensional manifold of constant interaction and showed that the IPFP is a fixed-point iteration on that manifold. Nevertheless, he assumed strictly positive observations. Generalization to tables with zero entries is still considered a hard and only partly solved problem.
An exhaustive treatment of the algorithm and its mathematical foundations can be found in the book of Bishop et al. (1975). The first general proof of convergence, built on non-trivial measure theoretic theorems and entropy minimization, is due to Csiszár (1975).
Relatively new results on convergence and error behavior have been published by Pukelsheim and Simeone (2009)
. They proved simple necessary and sufficient conditions for the convergence of the IPFP for arbitrary two-way tables (e.i. tables with zero entries) by analysing an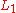 -error function.
-error function.
Other general algorithms can be modified to yield the same limit as the IPFP, for instance the Newton–Raphson method and
the EM algorithm. In most cases, IPFP is preferred due to its computational speed, numerical stability and algebraic simplicity.
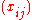 , where the cell values are assumed to be Poisson or multinomially distributed, we wish to estimate a decomposition
, where the cell values are assumed to be Poisson or multinomially distributed, we wish to estimate a decomposition  for all i and j such that
for all i and j such that 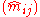 is the maximum likelihood
is the maximum likelihood
estimate (MLE) of the expected values leaving the marginals
leaving the marginals  and
and 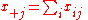 fixed. The assumption that the table factorizes in such a manner is known as the model of independence (I-model). Written in terms of a log-linear model
fixed. The assumption that the table factorizes in such a manner is known as the model of independence (I-model). Written in terms of a log-linear model
, we can write this assumption as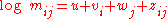 , where
, where 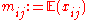 ,
,  and the interaction term vanishes, that is
and the interaction term vanishes, that is 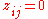 for all i and j.
for all i and j.
Choose initial values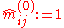 (different choices of initial values may lead to changes in convergence behavior), and for
(different choices of initial values may lead to changes in convergence behavior), and for  set
set
Notes:
Alternatively, we can estimate the row and column factors separately: Choose initial values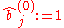 , and for
, and for  set
set
Setting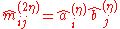 , the two variants of the algorithm are mathematically equivalent (can be seen by formal induction).
, the two variants of the algorithm are mathematically equivalent (can be seen by formal induction).
Notes:
Obviously, the I-model is a particular case of the Q-model.
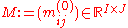 be the initial matrix with nonnegative entries,
be the initial matrix with nonnegative entries,  a vector of specified
a vector of specified
row marginals (e.i. row sums) and a vector of column marginals. We wish to compute a matrix
a vector of column marginals. We wish to compute a matrix 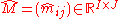 similar to M with predefined marginals, meaning
similar to M with predefined marginals, meaning
and
Define the diagonalization operator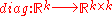 , which produces a (diagonal) matrix with its input vector on the main diagonal and zero elsewhere. Then, for
, which produces a (diagonal) matrix with its input vector on the main diagonal and zero elsewhere. Then, for  , set
, set
where
Finally, we obtain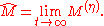
one would not implement actual matrix multiplication, since diagonal matrices are involved. Reducing the operations to the necessary ones,
it can easily be seen that RAS does the same as IPFP. The vaguely demanded 'similarity' can be explained as follows: IPFP (and thus RAS)
maintains the crossproduct ratios, e.i.
since
This property is sometimes called structure conservation and directly leads to the geometrical interpretation of contingency tables and the proof of convergence in the seminal paper of Fienberg (1970).
Nevertheless, direct factor estimation (algorithm 2) is under all circumstances the best way to deal with IPF: Whereas classical IPFP needs
elementary operations in each iteration step (including a row and a column fitting step), factor estimation needs only
operations being at least one order in magnitude faster than classical IPFP.
If unique MLEs exist, IPFP exhibits linear convergence in the worst case (Fienberg 1970), but exponential convergence has also been observed (Pukelsheim and Simeone 2009). If a direct estimator (i.e. a closed form of ) exists, IPFP converges after 2 iterations. If unique MLEs do not exist, IPFP converges toward the so-called extended MLEs by design (Haberman 1974), but convergence may be arbitrarily slow and often computationally infeasible.
) exists, IPFP converges after 2 iterations. If unique MLEs do not exist, IPFP converges toward the so-called extended MLEs by design (Haberman 1974), but convergence may be arbitrarily slow and often computationally infeasible.
If all observed values are strictly positive, existence and uniqueness of MLEs and therefore convergence is ensured.
or alternatively the likelihood-ratio test
(G-test
) statistic
Both statistics are asymptotically -distributed, where
-distributed, where 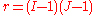 is the number of degrees of freedom.
is the number of degrees of freedom.
That is, if the p-value
s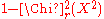 and
and  are not too small (> 0.05 for instance), there is no indication to discard the hypothesis of independence.
are not too small (> 0.05 for instance), there is no indication to discard the hypothesis of independence.
s):
For executing the classical IPFP, we first initialize the matrix with ones, leaving the marginals untouched:
Of course, the marginal sums do not correspond to the matrix anymore, but this is fixed in the next two iterations of IPFP. The first iteration deals with the row sums:
Note that, by definition, the row sums always constitute a perfect match after odd iterations, as do the column sums for even ones. The subsequent iteration updates the matrix column-wise:
Now, both row and column sums of the matrix match the given marginals again.
The p-value
of this matrix approximates to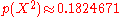 , meaning: gender and left-handedness/right-handedness can be considered independent.
, meaning: gender and left-handedness/right-handedness can be considered independent.
Contingency table
In statistics, a contingency table is a type of table in a matrix format that displays the frequency distribution of the variables...
such that the marginal totals remain fixed and the estimated table decomposes into an outer product
Outer product
In linear algebra, the outer product typically refers to the tensor product of two vectors. The result of applying the outer product to a pair of vectors is a matrix...
.
First introduced by Deming
W. Edwards Deming
William Edwards Deming was an American statistician, professor, author, lecturer and consultant. He is perhaps best known for his work in Japan...
and Stephan in 1940 (they proposed IPFP as an algorithm leading to a minimizer of the Pearson X-squared statistic, which it does not, and even failed to prove convergence), it has seen various extensions and related research. A rigorous proof of convergence by means of differential geometry is due to Fienberg
Stephen Fienberg
Stephen Elliott Fienberg is the Maurice Falk University Professor of Statistics and Social Science in the Department of Statistics, the Machine Learning Department and Cylab at Carnegie Mellon University....
(1970). He interpreted the family of contingency tables of constant crossproduct ratios as a particular (IJ − 1)-dimensional manifold of constant interaction and showed that the IPFP is a fixed-point iteration on that manifold. Nevertheless, he assumed strictly positive observations. Generalization to tables with zero entries is still considered a hard and only partly solved problem.
An exhaustive treatment of the algorithm and its mathematical foundations can be found in the book of Bishop et al. (1975). The first general proof of convergence, built on non-trivial measure theoretic theorems and entropy minimization, is due to Csiszár (1975).
Relatively new results on convergence and error behavior have been published by Pukelsheim and Simeone (2009)
. They proved simple necessary and sufficient conditions for the convergence of the IPFP for arbitrary two-way tables (e.i. tables with zero entries) by analysing an
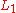 -error function.
-error function.Other general algorithms can be modified to yield the same limit as the IPFP, for instance the Newton–Raphson method and
the EM algorithm. In most cases, IPFP is preferred due to its computational speed, numerical stability and algebraic simplicity.
Algorithm 1 (classical IPFP)
Given a two-way (I × J)-table of counts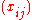 , where the cell values are assumed to be Poisson or multinomially distributed, we wish to estimate a decomposition
, where the cell values are assumed to be Poisson or multinomially distributed, we wish to estimate a decomposition  for all i and j such that
for all i and j such that 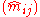 is the maximum likelihood
is the maximum likelihoodMaximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
estimate (MLE) of the expected values
 leaving the marginals
leaving the marginals  and
and 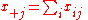 fixed. The assumption that the table factorizes in such a manner is known as the model of independence (I-model). Written in terms of a log-linear model
fixed. The assumption that the table factorizes in such a manner is known as the model of independence (I-model). Written in terms of a log-linear modelLog-linear model
A log-linear model is a mathematical model that takes the form of a function whose logarithm is a first-degree polynomial function of the parameters of the model, which makes it possible to apply linear regression...
, we can write this assumption as
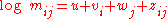 , where
, where 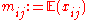 ,
,  and the interaction term vanishes, that is
and the interaction term vanishes, that is 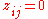 for all i and j.
for all i and j.Choose initial values
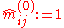 (different choices of initial values may lead to changes in convergence behavior), and for
(different choices of initial values may lead to changes in convergence behavior), and for  set
setNotes:
- Convergence does not depend on the actual distribution. Distributional assumptions are necessary for inferring that the limit
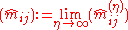 is an MLE indeed.
is an MLE indeed.
- IPFP can be manipulated to generate any positive marginals be replacing
 by the desired row marginal
by the desired row marginal 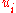 (analogously for the column marginals).
(analogously for the column marginals).
- IPFP can be extended to fit the model of quasi-independence (Q-model), where
 is known a priori for
is known a priori for 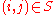 . Only the initial values have to be changed: Set
. Only the initial values have to be changed: Set 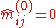 if
if 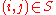 and 1 otherwise.
and 1 otherwise.
Algorithm 2 (factor estimation)
Assume the same setting as in the classical IPFP.Alternatively, we can estimate the row and column factors separately: Choose initial values
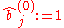 , and for
, and for  set
setSetting
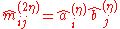 , the two variants of the algorithm are mathematically equivalent (can be seen by formal induction).
, the two variants of the algorithm are mathematically equivalent (can be seen by formal induction).Notes:
- In matrix notation, we can write
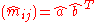 , where
, where 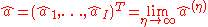 and
and 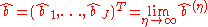 .
. - The factorization is not unique, since it is
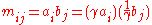 for all
for all  .
. - The factor totals remain constant, i.e.
 for all
for all  and
and 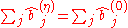 for all
for all  .
. - To fit the Q-model, where
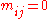 a priori for
a priori for 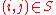 , set
, set 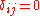 if (
if (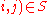 and
and 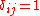 otherwise. Then
otherwise. Then
Obviously, the I-model is a particular case of the Q-model.
Algorithm 3 (RAS)
The Problem: Let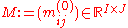 be the initial matrix with nonnegative entries,
be the initial matrix with nonnegative entries,  a vector of specified
a vector of specifiedrow marginals (e.i. row sums) and
 a vector of column marginals. We wish to compute a matrix
a vector of column marginals. We wish to compute a matrix 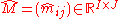 similar to M with predefined marginals, meaning
similar to M with predefined marginals, meaningand
Define the diagonalization operator
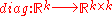 , which produces a (diagonal) matrix with its input vector on the main diagonal and zero elsewhere. Then, for
, which produces a (diagonal) matrix with its input vector on the main diagonal and zero elsewhere. Then, for  , set
, setwhere
Finally, we obtain
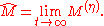
Discussion and comparison of the algorithms
Although RAS seems to be the solution of an entirely different problem, it is indeed identical to the classical IPFP. In practice,one would not implement actual matrix multiplication, since diagonal matrices are involved. Reducing the operations to the necessary ones,
it can easily be seen that RAS does the same as IPFP. The vaguely demanded 'similarity' can be explained as follows: IPFP (and thus RAS)
maintains the crossproduct ratios, e.i.
since

This property is sometimes called structure conservation and directly leads to the geometrical interpretation of contingency tables and the proof of convergence in the seminal paper of Fienberg (1970).
Nevertheless, direct factor estimation (algorithm 2) is under all circumstances the best way to deal with IPF: Whereas classical IPFP needs
elementary operations in each iteration step (including a row and a column fitting step), factor estimation needs only
operations being at least one order in magnitude faster than classical IPFP.
Existence and uniqueness of MLEs
Necessary and sufficient conditions for the existence and uniqueness of MLEs are complicated in the general case (see), but sufficient conditions for 2-dimensional tables are simple:- the marginals of the observed table do not vanish (that is,
 ) and
) and - the observed table is inseparable (e.i. the table does not permute to a block-diagonal shape).
If unique MLEs exist, IPFP exhibits linear convergence in the worst case (Fienberg 1970), but exponential convergence has also been observed (Pukelsheim and Simeone 2009). If a direct estimator (i.e. a closed form of
 ) exists, IPFP converges after 2 iterations. If unique MLEs do not exist, IPFP converges toward the so-called extended MLEs by design (Haberman 1974), but convergence may be arbitrarily slow and often computationally infeasible.
) exists, IPFP converges after 2 iterations. If unique MLEs do not exist, IPFP converges toward the so-called extended MLEs by design (Haberman 1974), but convergence may be arbitrarily slow and often computationally infeasible.If all observed values are strictly positive, existence and uniqueness of MLEs and therefore convergence is ensured.
Goodness of fit
Checking if the assumption of independence is adequate, one uses the Pearson X-squared statisticor alternatively the likelihood-ratio test
Likelihood-ratio test
In statistics, a likelihood ratio test is a statistical test used to compare the fit of two models, one of which is a special case of the other . The test is based on the likelihood ratio, which expresses how many times more likely the data are under one model than the other...
(G-test
G-test
In statistics, G-tests are likelihood-ratio or maximum likelihood statistical significance tests that are increasingly being used in situations where chi-squared tests were previously recommended....
) statistic
-
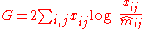 .
.
Both statistics are asymptotically
 -distributed, where
-distributed, where 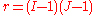 is the number of degrees of freedom.
is the number of degrees of freedom.That is, if the p-value
P-value
In statistical significance testing, the p-value is the probability of obtaining a test statistic at least as extreme as the one that was actually observed, assuming that the null hypothesis is true. One often "rejects the null hypothesis" when the p-value is less than the significance level α ,...
s
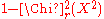 and
and  are not too small (> 0.05 for instance), there is no indication to discard the hypothesis of independence.
are not too small (> 0.05 for instance), there is no indication to discard the hypothesis of independence.Interpretation
If the rows correspond to different values of property A, and the columns correspond to different values of property B, and the hypothesis of independence is not discarded, the properties A and B are considered independent.Example
Consider a table of observations (taken from the entry on contingency tableContingency table
In statistics, a contingency table is a type of table in a matrix format that displays the frequency distribution of the variables...
s):
| right-handed | left-handed | TOTAL | |
| male | 43 | 9 | 52 |
| female | 44 | 4 | 48 |
| TOTAL | 87 | 13 | 100 |
For executing the classical IPFP, we first initialize the matrix with ones, leaving the marginals untouched:
| right-handed | left-handed | TOTAL | |
| male | 1 | 1 | 52 |
| female | 1 | 1 | 48 |
| TOTAL | 87 | 13 | 100 |
Of course, the marginal sums do not correspond to the matrix anymore, but this is fixed in the next two iterations of IPFP. The first iteration deals with the row sums:
| right-handed | left-handed | TOTAL | |
| male | 26 | 26 | 52 |
| female | 24 | 24 | 48 |
| TOTAL | 87 | 13 | 100 |
Note that, by definition, the row sums always constitute a perfect match after odd iterations, as do the column sums for even ones. The subsequent iteration updates the matrix column-wise:
| right-handed | left-handed | TOTAL | |
| male | 45.24 | 6.76 | 52 |
| female | 41.76 | 6.24 | 48 |
| TOTAL | 87 | 13 | 100 |
Now, both row and column sums of the matrix match the given marginals again.
The p-value
P-value
In statistical significance testing, the p-value is the probability of obtaining a test statistic at least as extreme as the one that was actually observed, assuming that the null hypothesis is true. One often "rejects the null hypothesis" when the p-value is less than the significance level α ,...
of this matrix approximates to
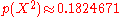 , meaning: gender and left-handedness/right-handedness can be considered independent.
, meaning: gender and left-handedness/right-handedness can be considered independent.