Intersection of a polyhedron with a line
Encyclopedia
In computational geometry
, the intersection of a polyhedron with a line is the problem of computing the intersection
of a convex polyhedron and a ray in Euclidean space
. This problem has important applications in computer graphics
, optimization
, and even in some Monte Carlo methods.
is defined as the intersection of a finite number of halfspaces. That is, a convex polyhedron is the set of solutions of a system of inequation
s of the form
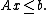
The formal statement of our problem is to find the intersection of the set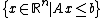
with the line defined by 
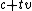, where 
and 
.
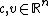such that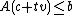 
, which is equivalent to finding a 
such that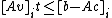
for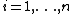
.
Thus, we can bound
as follows: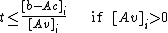
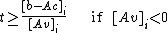
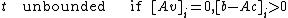
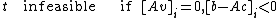
The last two lines follow from the cases when the direction vector
is parallel to the halfplane defined by the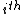 
row of 
: 
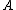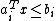. In the second to last case, the point 
is on the inside of the halfspace; in the last case, the point 
is on the outside of the halfspace, and so 
will always be infeasible.
As such, we can find
as all points in the region (so long as we do not have the fourth case from above)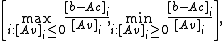
which will be empty if there is no intersection.
Computational geometry
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational...
, the intersection of a polyhedron with a line is the problem of computing the intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of a convex polyhedron and a ray in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. This problem has important applications in computer graphics
Computer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
, optimization
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
, and even in some Monte Carlo methods.
Statement of the problem
In general, a convex polyhedronPolyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
is defined as the intersection of a finite number of halfspaces. That is, a convex polyhedron is the set of solutions of a system of inequation
Inequation
In mathematics, an inequation is a statement that two objects or expressions are not the same, or do not represent the same value. This relation is written with a crossed-out equal sign as inx \neq y....
s of the form
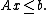
The formal statement of our problem is to find the intersection of the set
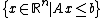with the line defined by 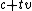, where and 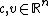.General solution
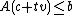To this end, we would like to find such that , which is equivalent to finding a such that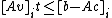for
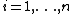.Thus, we can bound
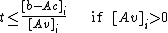
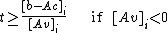
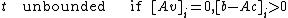
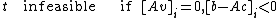
as follows:The last two lines follow from the cases when the direction vector
is parallel to the halfplane defined by the 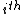row of 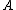: 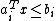. In the second to last case, the point is on the inside of the halfspace; in the last case, the point is on the outside of the halfspace, and so will always be infeasible.As such, we can find
as all points in the region (so long as we do not have the fourth case from above)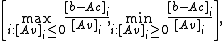which will be empty if there is no intersection.