
Inseparable differential equation
Encyclopedia
In mathematics
, an inseparable differential equation is an ordinary differential equation
that cannot be solved by using separation of variables
. To solve an inseparable differential equation one can employ a number of other methods, like the Laplace transform, substitution, etc.
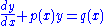
Now we will define a special factorial, μ as
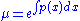
Thus:

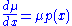
From here we can solve the equation using the above definition:
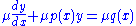

(using the product rule in reverse)
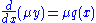

Finally, we obtain:

This can be used to solve most all inseparable equations containing no y to a degree other than one. For example, solving the inseparable equation:

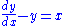
By arranging in the form required, we obtain:
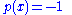
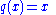

Now all that is necessary is to find the value of μ to plug into our original equation of
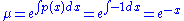
Plugging this into the original equation and simplifying gives us our final answer:
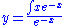
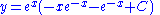
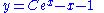
Consider for example the inseparable equation

Let us solve it using the Laplace transform. One has that
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an inseparable differential equation is an ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
that cannot be solved by using separation of variables
Separation of variables
In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....
. To solve an inseparable differential equation one can employ a number of other methods, like the Laplace transform, substitution, etc.
Examples
Consider the general inseparable equation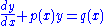
Now we will define a special factorial, μ as
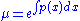
Thus:

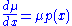
From here we can solve the equation using the above definition:
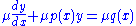

(using the product rule in reverse)
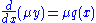

Finally, we obtain:

This can be used to solve most all inseparable equations containing no y to a degree other than one. For example, solving the inseparable equation:

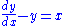
By arranging in the form required, we obtain:
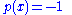
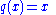

Now all that is necessary is to find the value of μ to plug into our original equation of

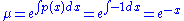
Plugging this into the original equation and simplifying gives us our final answer:
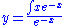
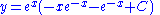
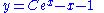
Consider for example the inseparable equation

Let us solve it using the Laplace transform. One has that
-
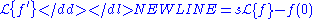
-
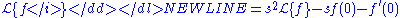
-
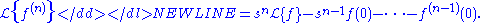
Using the convenience that Laplace transforms follow the rules of linearity, one can solve the above example for y by performing a Laplace transform on both sides of the differential equation, substituting in the initial values, solving for the transformed function, and then performing an inverse transform.
For the above example, assume initial values are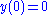 and
and 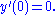 Then,
Then,
It follows that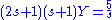
or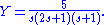
Now one can just take the inverse Laplace transform of Y to get the solution y to the original equation.
See also
- examples of differential equationsExamples of differential equationsDifferential equations arise in many problems in physics, engineering, and other sciences. The following examples show how to solve differential equations in a few simple cases when an exact solution exists....
- method of variation of parametersMethod of variation of parametersIn mathematics, variation of parameters, also known as variation of constants, is a general method to solve inhomogeneous linear ordinary differential equations...
-
-
-


