
Infinity Laplacian
Encyclopedia
In mathematics
, the infinity Laplace (or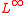 -Laplace) operator is a 2nd-order partial differential operator, commonly abbreviated
-Laplace) operator is a 2nd-order partial differential operator, commonly abbreviated 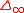 . It is alternately defined by
. It is alternately defined by
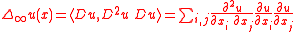
or
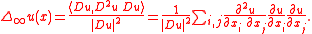
The first version has the advantage of being formally simpler, while the second version has the advantage of being linear, hence much more natural. Verbally, the second version is the second derivative in the direction of the gradient. In the case of the infinity Laplace equation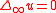 , the two definitions are equivalent.
, the two definitions are equivalent.
A fundamental property of the operator is that functions that should naturally be considered as solutions to the equation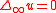 , i.e., infinity harmonic functions, are often not twice differentiable. Hence the equation should be understood in the viscosity sense.
, i.e., infinity harmonic functions, are often not twice differentiable. Hence the equation should be understood in the viscosity sense.
The infinity Laplace operator first arose in the study of absolute minimizers for , and it can be viewed in a certain sense as the limit of the p-Laplacian
, and it can be viewed in a certain sense as the limit of the p-Laplacian
as . More recently, viscosity solutions to the infinity Laplace equation have been identified with the payoff functions from randomized tug-of-war games
. More recently, viscosity solutions to the infinity Laplace equation have been identified with the payoff functions from randomized tug-of-war games
. The game theory point of view has significantly improved the understanding of the partial differential equation
itself.
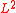 -harmonic function
-harmonic function
s is the mean value property. That has a natural and important discrete version: a real-valued function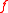 on a finite or infinite graph
on a finite or infinite graph
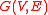 is discrete harmonic on a subset
is discrete harmonic on a subset 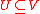 if
if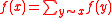
for all . Similarly, the vanishing second derivative in the direction of the gradient has a natural discrete version:
. Similarly, the vanishing second derivative in the direction of the gradient has a natural discrete version:
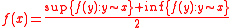 .
.
In this equation, we used sup and inf instead of max and min because the graph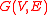 does not have to be locally finite (i.e., to have finite degrees): a key example is when
does not have to be locally finite (i.e., to have finite degrees): a key example is when 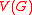 is the set of points in a domain in
is the set of points in a domain in 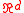 , and
, and 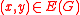 if their Euclidean distance is at most
if their Euclidean distance is at most  . The importance of this example lies in the following.
. The importance of this example lies in the following.
Consider a bounded open set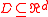 with smooth boundary
with smooth boundary  , and a continuous function
, and a continuous function  . In the
. In the 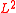 -case, an approximation of the harmonic extension of f to D is given by taking a lattice
-case, an approximation of the harmonic extension of f to D is given by taking a lattice 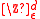 with small mesh size
with small mesh size  , letting
, letting 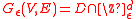 and
and 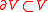 be the set of vertices with degree less than 2d, taking a natural approximation
be the set of vertices with degree less than 2d, taking a natural approximation  , and then taking the unique discrete harmonic extension of
, and then taking the unique discrete harmonic extension of 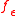 to V. However, it is easy to see by examples that this does not work for the
to V. However, it is easy to see by examples that this does not work for the 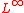 -case. Instead, as it turns out, one should take the continuum graph with all edges of length at most
-case. Instead, as it turns out, one should take the continuum graph with all edges of length at most  , mentioned above.
, mentioned above.
Now, a probabilistic way of looking at the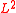 -harmonic extension of
-harmonic extension of 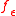 from
from 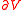 to
to 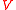 is that
is that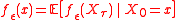 ,
,
where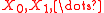 is the simple random walk on
is the simple random walk on 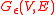 started at
started at  , and
, and  is the hitting time
is the hitting time
of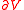 .
.
For the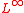 -case, we need game theory
-case, we need game theory
. A token is started at location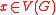 , and
, and 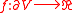 is given. There are two players, in each turn they flip a fair coin, and the winner can move the token to any neighbour of the current location. The game ends when the token reaches
is given. There are two players, in each turn they flip a fair coin, and the winner can move the token to any neighbour of the current location. The game ends when the token reaches 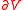 at some time
at some time  and location
and location 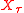 , at which point the first player gets the amount
, at which point the first player gets the amount 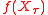 from the second player. Therefore, the first player wants to maximize
from the second player. Therefore, the first player wants to maximize 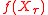 , while the second player wants to minimize it. If both players play optimally (which has a well-defined meaning in game theory), the expected payoff
, while the second player wants to minimize it. If both players play optimally (which has a well-defined meaning in game theory), the expected payoff  to the first player is a discrete infinity harmonic function, as defined above.
to the first player is a discrete infinity harmonic function, as defined above.
There is a game theory approach to the p-Laplacian
, too, interpolating between simple random walk and the above random tug-of-war game.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the infinity Laplace (or
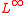 -Laplace) operator is a 2nd-order partial differential operator, commonly abbreviated
-Laplace) operator is a 2nd-order partial differential operator, commonly abbreviated 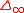 . It is alternately defined by
. It is alternately defined by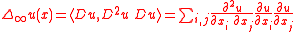
or
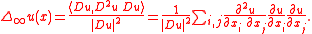
The first version has the advantage of being formally simpler, while the second version has the advantage of being linear, hence much more natural. Verbally, the second version is the second derivative in the direction of the gradient. In the case of the infinity Laplace equation
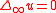 , the two definitions are equivalent.
, the two definitions are equivalent.A fundamental property of the operator is that functions that should naturally be considered as solutions to the equation
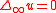 , i.e., infinity harmonic functions, are often not twice differentiable. Hence the equation should be understood in the viscosity sense.
, i.e., infinity harmonic functions, are often not twice differentiable. Hence the equation should be understood in the viscosity sense.The infinity Laplace operator first arose in the study of absolute minimizers for
 , and it can be viewed in a certain sense as the limit of the p-Laplacian
, and it can be viewed in a certain sense as the limit of the p-LaplacianP-Laplacian
In mathematics, the p-Laplacian, or the p-Laplace operator, is a quasilinear elliptic partial differential operator of 2nd order. It is a generalization of the Laplace operator, where p is allowed to range over 1...
as
 . More recently, viscosity solutions to the infinity Laplace equation have been identified with the payoff functions from randomized tug-of-war games
. More recently, viscosity solutions to the infinity Laplace equation have been identified with the payoff functions from randomized tug-of-war gamesDifferential game
In game theory, differential games are a group of problems related to the modeling and analysis of conflict in the context of a dynamical system. The problem usually consists of two actors, a pursuer and an evader, with conflicting goals...
. The game theory point of view has significantly improved the understanding of the partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
itself.
Discrete version and game theory
A defining property of the usual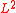 -harmonic function
-harmonic functionHarmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
s is the mean value property. That has a natural and important discrete version: a real-valued function
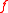 on a finite or infinite graph
on a finite or infinite graphGraph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
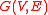 is discrete harmonic on a subset
is discrete harmonic on a subset 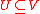 if
if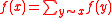
for all
 . Similarly, the vanishing second derivative in the direction of the gradient has a natural discrete version:
. Similarly, the vanishing second derivative in the direction of the gradient has a natural discrete version: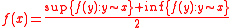 .
.In this equation, we used sup and inf instead of max and min because the graph
 does not have to be locally finite (i.e., to have finite degrees): a key example is when
does not have to be locally finite (i.e., to have finite degrees): a key example is when  is the set of points in a domain in
is the set of points in a domain in 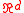 , and
, and 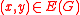 if their Euclidean distance is at most
if their Euclidean distance is at most  . The importance of this example lies in the following.
. The importance of this example lies in the following.Consider a bounded open set
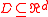 with smooth boundary
with smooth boundary  , and a continuous function
, and a continuous function  . In the
. In the 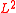 -case, an approximation of the harmonic extension of f to D is given by taking a lattice
-case, an approximation of the harmonic extension of f to D is given by taking a lattice 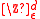 with small mesh size
with small mesh size  , letting
, letting 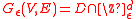 and
and 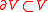 be the set of vertices with degree less than 2d, taking a natural approximation
be the set of vertices with degree less than 2d, taking a natural approximation  , and then taking the unique discrete harmonic extension of
, and then taking the unique discrete harmonic extension of 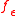 to V. However, it is easy to see by examples that this does not work for the
to V. However, it is easy to see by examples that this does not work for the 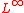 -case. Instead, as it turns out, one should take the continuum graph with all edges of length at most
-case. Instead, as it turns out, one should take the continuum graph with all edges of length at most  , mentioned above.
, mentioned above.Now, a probabilistic way of looking at the
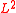 -harmonic extension of
-harmonic extension of 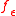 from
from 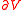 to
to 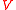 is that
is that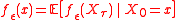 ,
,where
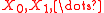 is the simple random walk on
is the simple random walk on 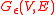 started at
started at  , and
, and  is the hitting time
is the hitting timeHitting time
In the study of stochastic processes in mathematics, a hitting time is a particular instance of a stopping time, the first time at which a given process "hits" a given subset of the state space...
of
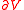 .
.For the
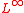 -case, we need game theory
-case, we need game theoryGame theory
Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...
. A token is started at location
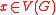 , and
, and 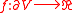 is given. There are two players, in each turn they flip a fair coin, and the winner can move the token to any neighbour of the current location. The game ends when the token reaches
is given. There are two players, in each turn they flip a fair coin, and the winner can move the token to any neighbour of the current location. The game ends when the token reaches 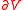 at some time
at some time  and location
and location 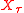 , at which point the first player gets the amount
, at which point the first player gets the amount 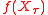 from the second player. Therefore, the first player wants to maximize
from the second player. Therefore, the first player wants to maximize 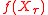 , while the second player wants to minimize it. If both players play optimally (which has a well-defined meaning in game theory), the expected payoff
, while the second player wants to minimize it. If both players play optimally (which has a well-defined meaning in game theory), the expected payoff  to the first player is a discrete infinity harmonic function, as defined above.
to the first player is a discrete infinity harmonic function, as defined above.There is a game theory approach to the p-Laplacian
P-Laplacian
In mathematics, the p-Laplacian, or the p-Laplace operator, is a quasilinear elliptic partial differential operator of 2nd order. It is a generalization of the Laplace operator, where p is allowed to range over 1...
, too, interpolating between simple random walk and the above random tug-of-war game.

