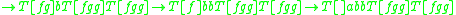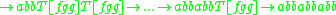Indexed grammar
Encyclopedia
An indexed grammar is a formal grammar
which describes indexed language
s. They have three disjoint sets of symbols: the usual terminals and nonterminals, as well as index symbols, which appear only in intermediate derivation steps on a stack associated with the non-terminals of that step.
The problem of determining whether a string is recognized by an indexed grammar is NP-complete
.
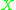with some index symbols 
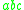on its stack, can be denoted as 
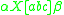(using the [ and ] as metasymbols to denote the stack). In an indexed grammar, the application of a production rule such as 
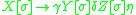would rewrite the string by replacing 
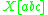with 
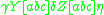, which copies the stack symbols 
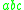from X to each non-terminal in its replacement — Y and Z in this case. In the process, a symbol can be pushed to, or popped from, the stack before the stack is copied to the introduced non-terminals, which would be specified in the rule for the rewriting operation.
:
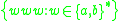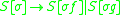
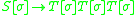
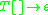
The production for "abbabbabb" is then
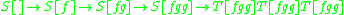
The language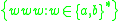
is generable by an indexed grammar, but not by a linear indexed grammar, while 
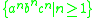is generable by a linear indexed grammar.
denote an arbitrary collection of stack symbols, we can define a grammar for the language 
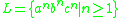as
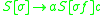
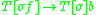
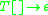
To derive the string "abc" we have the production steps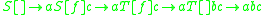
.
Similarly, for "aabbcc":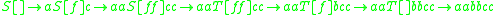
.
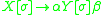, modulo the push/pop part of a rewrite rule. The symbols 
and 
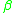represent strings of terminal and/or non-terminal symbols, and any non-terminal symbol in either must have an empty stack, by the definition of a LIG. This is, of course, counter to how IGs are defined: in an IG, the non-terminals whose stacks are not being pushed to or popped from must have exactly the same stack as the rewritten non-terminal. Thus, somehow, we need to have non-terminals in 
and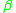 
which, despite having non-empty stacks, behave as if they had empty stacks.
Let's consider the rule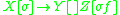
as an example case. In converting this to an IG, the replacement for 
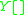must be some 
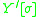that behaves exactly like 
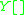regardless of what 
is. To achieve this, we can simply have a pair of rules that takes any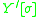 
where 
is not empty, and pops symbols from the stack. Then, when the stack is empty, it can be rewritten as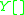 
.
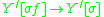
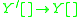
We can apply this in general to derive an IG from an LIG. So for example if the LIG for the language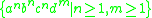
is as follows:
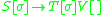
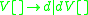
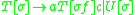
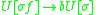
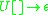
The sentential rule here is not an IG rule, but using the above conversion algorithm, we can define new rules for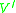
, changing the grammar to:
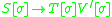
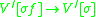
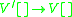
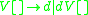
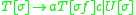
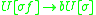
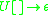
Each rule now fits the definition of an IG, in which all the non-terminals in the right hand side of a rewrite rule receive a copy of the rewritten symbol's stack. The indexed grammars are therefore able to describe all the languages that linearly indexed grammars can describe.
, Tree-adjoining Grammars
, and Head Grammars
are weakly equivalent
formalisms, in that the all define the same string languages.
The general rule schema for a binarily distributing rule of DIG is the form
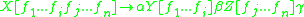
Where
, 
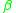, and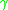 
are arbitrary terminal strings. For a ternarily distributing string:
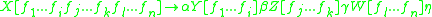
And so forth for higher numbers of non-terminals in the right hand side of the rewrite rule. In general, if there are N non-terminals in the right hand side of a rewrite rule, the stack is partitioned N ways and distributed amongst the new non-terminals. Notice that there is a special case where a partition is empty, which effectively makes the rule a LIG rule. The Distributed Index languages are therefore a superset of the Linearly Indexed languages.
Formal grammar
A formal grammar is a set of formation rules for strings in a formal language. The rules describe how to form strings from the language's alphabet that are valid according to the language's syntax...
which describes indexed language
Indexed language
Indexed languages are a class of formal languages discovered by Alfred Aho; they are described by indexed grammars and can be recognized by nested stack automatons....
s. They have three disjoint sets of symbols: the usual terminals and nonterminals, as well as index symbols, which appear only in intermediate derivation steps on a stack associated with the non-terminals of that step.
The problem of determining whether a string is recognized by an indexed grammar is NP-complete
NP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
.
Description
A string with a non-terminal symbol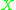 with some index symbols 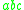on its stack, can be denoted as 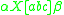(using the [ and ] as metasymbols to denote the stack). In an indexed grammar, the application of a production rule such as 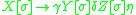would rewrite the string by replacing 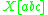with 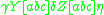, which copies the stack symbols 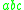from X to each non-terminal in its replacement — Y and Z in this case. In the process, a symbol can be pushed to, or popped from, the stack before the stack is copied to the introduced non-terminals, which would be specified in the rule for the rewriting operation.Example
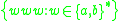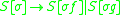
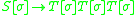
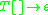
In practice, stacks of indices can count and remember what rules were applied and in which order. For example, indexed grammars can describe the context-sensitive language of word triples:The production for "abbabbabb" is then
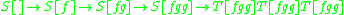
Linear indexed grammars
Gerald Gazdar has defined a second class, the linear indexed grammars, by requiring that at most one nonterminal in each production be specified as receiving the stack, whereas in a normal indexed grammar, all nonterminals receive copies of the stack. He showed that this new class of grammars defines a strictly smaller class of languages, the mildly context sensitive languages. Membership in a linear indexed grammar can be decided in polynomial time.The language
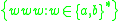is generable by an indexed grammar, but not by a linear indexed grammar, while 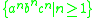is generable by a linear indexed grammar.Example
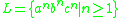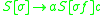
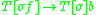
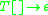
Letting denote an arbitrary collection of stack symbols, we can define a grammar for the language asTo derive the string "abc" we have the production steps
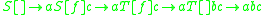.Similarly, for "aabbcc":
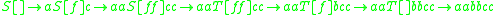.Computational Power
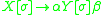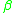The linearly indexed languages are a subset of the indexed languages, and thus all LIGs can be recoded as IGs, making the LIGs strictly less powerful than the IGs. A conversion from a LIG to an IG is relatively simple. LIG rules in general look approximately like, modulo the push/pop part of a rewrite rule. The symbols and represent strings of terminal and/or non-terminal symbols, and any non-terminal symbol in either must have an empty stack, by the definition of a LIG. This is, of course, counter to how IGs are defined: in an IG, the non-terminals whose stacks are not being pushed to or popped from must have exactly the same stack as the rewritten non-terminal. Thus, somehow, we need to have non-terminals in and 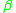which, despite having non-empty stacks, behave as if they had empty stacks.Let's consider the rule
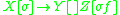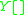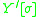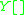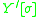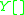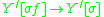
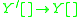
as an example case. In converting this to an IG, the replacement for must be some that behaves exactly like regardless of what is. To achieve this, we can simply have a pair of rules that takes any where is not empty, and pops symbols from the stack. Then, when the stack is empty, it can be rewritten as .We can apply this in general to derive an IG from an LIG. So for example if the LIG for the language
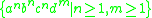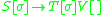
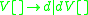
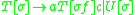
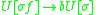
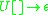
is as follows:The sentential rule here is not an IG rule, but using the above conversion algorithm, we can define new rules for
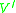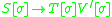
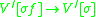
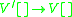
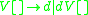
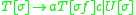
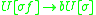
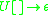
, changing the grammar to:Each rule now fits the definition of an IG, in which all the non-terminals in the right hand side of a rewrite rule receive a copy of the rewritten symbol's stack. The indexed grammars are therefore able to describe all the languages that linearly indexed grammars can describe.
Equivalencies
Vijay-Shanker and Weir (1994) demonstrates that Linear Indexed Grammars, Combinatory Categorial GrammarsCombinatory categorial grammar
Combinatory categorial grammar is an efficiently parseable, yet linguistically expressive grammar formalism. It has a transparent interface between surface syntax and underlying semantic representation, including predicate-argument structure, quantification and information structure.CCG relies on...
, Tree-adjoining Grammars
Tree-adjoining grammar
Tree-adjoining grammar is a grammar formalism defined by Aravind Joshi. Tree-adjoining grammars are somewhat similar to context-free grammars, but the elementary unit of rewriting is the tree rather than the symbol...
, and Head Grammars
Head grammar
Head Grammar is a grammar formalism introduced in Carl Pollard as an extension of the Context-free grammar class of grammars. The class of head grammars is a subset of the linear context-free rewriting systems....
are weakly equivalent
Weak equivalence
-Mathematics:In mathematics, a weak equivalence is a notion from homotopy theory which in some sense identifies objects that have the same basic "shape"...
formalisms, in that the all define the same string languages.
Distributed Index (DI) grammars
Another form of indexed grammars, introduced by Staudacher (1993), is the class of Distributed Index grammars (DIGs). What distinguishes DIGs from Aho's Indexed Grammars is the propagation of indexes. Unlike Aho's IGs, which distribute the whole symbol stack to all non-terminals during a rewrite operation, DIGs divide the stack into substacks and distributes the substacks to selected non-terminals.The general rule schema for a binarily distributing rule of DIG is the form
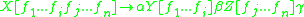
Where
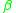, , and 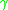are arbitrary terminal strings. For a ternarily distributing string: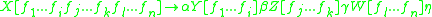And so forth for higher numbers of non-terminals in the right hand side of the rewrite rule. In general, if there are N non-terminals in the right hand side of a rewrite rule, the stack is partitioned N ways and distributed amongst the new non-terminals. Notice that there is a special case where a partition is empty, which effectively makes the rule a LIG rule. The Distributed Index languages are therefore a superset of the Linearly Indexed languages.