
Head grammar
Encyclopedia
Head Grammar is a grammar formalism introduced in Carl Pollard
(1984) as an extension of the Context-free grammar
class of grammars. The class of head grammars is a subset of the linear context-free rewriting systems.
One typical way of defining head grammars is to replace the terminal strings of CFGs
with indexed terminal strings, where the index denotes the "head" word of the string. Thus, for example, a CF rule such as might instead be
might instead be 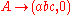 , where the 0th terminal, the a, is the head of the resulting terminal string. For convenience of notation, such a rule could be written as just the terminal string, with the head terminal denoted by some sort of mark, as in
, where the 0th terminal, the a, is the head of the resulting terminal string. For convenience of notation, such a rule could be written as just the terminal string, with the head terminal denoted by some sort of mark, as in  .
.
Two fundamental operations are then added to all rewrite rules: wrapping and concatenation.
Let and
and  be terminal strings headed by x and y, respectively.
be terminal strings headed by x and y, respectively.
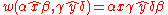
Let ,
,  , and
, and  be terminal strings headed by x, y, and z, respectively.
be terminal strings headed by x, y, and z, respectively.
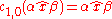
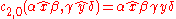
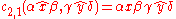
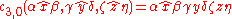
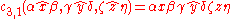
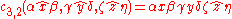
And so on for . One can sum up the pattern here simply as "concatenate some number of terminal strings m, with the head of string n designated as the head of the resulting string".
. One can sum up the pattern here simply as "concatenate some number of terminal strings m, with the head of string n designated as the head of the resulting string".
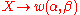
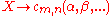
where ,
, 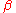 , ... are each either a terminal string or a non-terminal symbol.
, ... are each either a terminal string or a non-terminal symbol.
 . We can define the grammar as follows:
. We can define the grammar as follows:
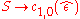
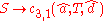
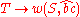
The derivation for "abcd" is thus:
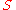
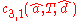
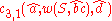
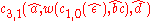
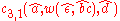
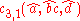
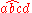
And for "aabbccdd":

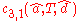
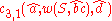
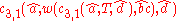
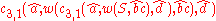
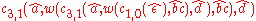
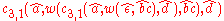
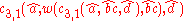
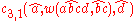
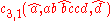
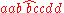
, Combinatory Categorial Grammars
, Tree-adjoining Grammars
, and Head Grammars are weakly equivalent
formalisms, in that they all define the same string languages.
Carl Pollard
Carl Jesse Pollard is a Professor of Linguistics at the Ohio State University. He is the inventor of Head grammar and Higher-order grammar, as well as co-inventor of Head-driven phrase structure grammar . He is currently also working on Convergent Grammar . He has written numerous books and...
(1984) as an extension of the Context-free grammar
Context-free grammar
In formal language theory, a context-free grammar is a formal grammar in which every production rule is of the formwhere V is a single nonterminal symbol, and w is a string of terminals and/or nonterminals ....
class of grammars. The class of head grammars is a subset of the linear context-free rewriting systems.
One typical way of defining head grammars is to replace the terminal strings of CFGs
Context-free grammar
In formal language theory, a context-free grammar is a formal grammar in which every production rule is of the formwhere V is a single nonterminal symbol, and w is a string of terminals and/or nonterminals ....
with indexed terminal strings, where the index denotes the "head" word of the string. Thus, for example, a CF rule such as
 might instead be
might instead be 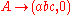 , where the 0th terminal, the a, is the head of the resulting terminal string. For convenience of notation, such a rule could be written as just the terminal string, with the head terminal denoted by some sort of mark, as in
, where the 0th terminal, the a, is the head of the resulting terminal string. For convenience of notation, such a rule could be written as just the terminal string, with the head terminal denoted by some sort of mark, as in  .
.Two fundamental operations are then added to all rewrite rules: wrapping and concatenation.
Wrapping
Wrapping is an operation on two headed strings defined as follows:Let
 and
and  be terminal strings headed by x and y, respectively.
be terminal strings headed by x and y, respectively.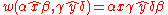
Concatenation
Concatenation is a family of operations on n > 0 headed strings, defined for n = 1, 2, 3 as follows:Let
 ,
,  , and
, and  be terminal strings headed by x, y, and z, respectively.
be terminal strings headed by x, y, and z, respectively.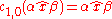
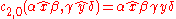
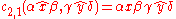
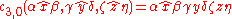
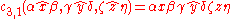
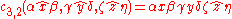
And so on for
 . One can sum up the pattern here simply as "concatenate some number of terminal strings m, with the head of string n designated as the head of the resulting string".
. One can sum up the pattern here simply as "concatenate some number of terminal strings m, with the head of string n designated as the head of the resulting string".Form of Rules
Head Grammar rules are defined in terms of these two operations, with rules taking either of the forms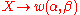
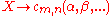
where
 ,
, 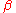 , ... are each either a terminal string or a non-terminal symbol.
, ... are each either a terminal string or a non-terminal symbol.Example
Head Grammars are capable of generating the language . We can define the grammar as follows:
. We can define the grammar as follows: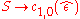
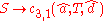
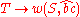
The derivation for "abcd" is thus:
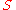
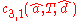
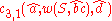
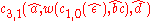
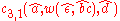
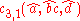
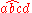
And for "aabbccdd":

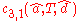
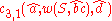
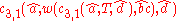
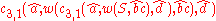
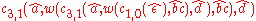
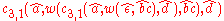
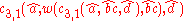
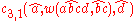
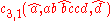
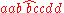
Equivalencies
Vijay-Shanker and Weir (1994) demonstrates that Linear Indexed GrammarsIndexed grammar
An indexed grammar is a formal grammar which describes indexed languages. They have three disjoint sets of symbols: the usual terminals and nonterminals, as well as index symbols, which appear only in intermediate derivation steps on a stack associated with the non-terminals of that step.The...
, Combinatory Categorial Grammars
Combinatory categorial grammar
Combinatory categorial grammar is an efficiently parseable, yet linguistically expressive grammar formalism. It has a transparent interface between surface syntax and underlying semantic representation, including predicate-argument structure, quantification and information structure.CCG relies on...
, Tree-adjoining Grammars
Tree-adjoining grammar
Tree-adjoining grammar is a grammar formalism defined by Aravind Joshi. Tree-adjoining grammars are somewhat similar to context-free grammars, but the elementary unit of rewriting is the tree rather than the symbol...
, and Head Grammars are weakly equivalent
Weak equivalence
-Mathematics:In mathematics, a weak equivalence is a notion from homotopy theory which in some sense identifies objects that have the same basic "shape"...
formalisms, in that they all define the same string languages.

