Combinatory categorial grammar
Encyclopedia
Combinatory categorial grammar
(CCG) is an efficiently parseable, yet linguistically expressive grammar formalism. It has a transparent interface between surface syntax and underlying semantic representation, including predicate-argument structure, quantification and information structure.
CCG relies on combinatory logic
, which has the same expressive power as the lambda calculus
, but builds its expressions differently. The first linguistic and psycholinguistic arguments for basing the grammar on combinators were put forth by Steedman
and Szabolcsi
. More recent prominent proponents of the approach are Jacobson and Baldridge.
For example, the combinator B (the compositor) is useful in creating long-distance dependencies, as in "Who do you think Mary is talking about?" and the combinator W (the duplicator) is useful as the lexical interpretation of reflexive pronouns, as in "Mary talks about herself". Together with I (the identity mapping) and C (the permutator) these form a set of primitive, non-interdefinable combinators. Jacobson interprets personal pronouns as the combinator I, and their binding is aided by a complex combinator Z, as in "Mary lost her way". Z is definable using W and B.
style proofs. The goal of the proof is to find some way of applying the combinators to a sequence of lexical items until no lexical item is unused in the proof. The resulting type after the proof is complete is the type of the whole expression. Thus, proving that some sequence of words is a sentence of some language amounts to proving that the words reduce to the type S.
The complex types, schematizable as X/Y and X\Y, denote functor types that take an argument of type Y and return an object of type X. A forward slash denotes that the argument should appear to the right, while a backslash denotes that the argument should appear on the left. Any type can stand in for the X and Y here, making syntactic types in CCG a recursive type system.
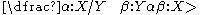
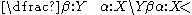
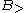for forward composition and 
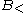for backward composition, are similar to function composition from mathematics, and can be defined as follows:
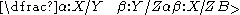
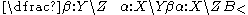
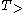for forward type-raising and 
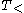for backward type-raising, take argument types (usually primitive types) to functor types, which take as their argument the functors that, before type-raising, would have taken them as arguments.
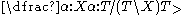
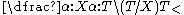
Let the types of these lexical items be
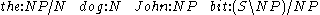
We can perform the simplest proof (changing notation slightly for brevity) as:
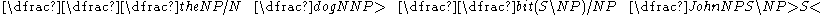
Opting to type-raise and compose some, we could get a fully incremental, left-to-right proof:
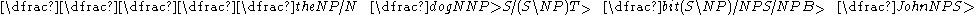
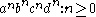. Examples of this are unfortunately too complicated to provide here, but can be found in Vijay-Shanker and Weir (1994).
, and Head Grammars
are weakly equivalent
formalisms, in that they all define the same string languages.
Categorial grammar
Categorial grammar is a term used for a family of formalisms in natural language syntax motivated by the principle of compositionality and organized according to the view that syntactic constituents should generally combine as functions or according to a function-argument relationship...
(CCG) is an efficiently parseable, yet linguistically expressive grammar formalism. It has a transparent interface between surface syntax and underlying semantic representation, including predicate-argument structure, quantification and information structure.
CCG relies on combinatory logic
Combinatory logic
Combinatory logic is a notation introduced by Moses Schönfinkel and Haskell Curry to eliminate the need for variables in mathematical logic. It has more recently been used in computer science as a theoretical model of computation and also as a basis for the design of functional programming...
, which has the same expressive power as the lambda calculus
Lambda calculus
In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
, but builds its expressions differently. The first linguistic and psycholinguistic arguments for basing the grammar on combinators were put forth by Steedman
Mark Steedman
Mark Jerome Steedman, FBA, FRSE is a computational linguist and cognitive scientist.Steedman graduated from the University of Sussex in 1968, with a B.Sc in Experimental Psychology, and from the University of Edinburgh in 1973, with a Ph.D. in Artificial Intelligence Mark Jerome Steedman, FBA,...
and Szabolcsi
Anna Szabolcsi
Anna Szabolcsi is a linguist whose research has focused on semantics, syntax, and the syntax-semantics interface. She was born and educated in Hungary...
. More recent prominent proponents of the approach are Jacobson and Baldridge.
For example, the combinator B (the compositor) is useful in creating long-distance dependencies, as in "Who do you think Mary is talking about?" and the combinator W (the duplicator) is useful as the lexical interpretation of reflexive pronouns, as in "Mary talks about herself". Together with I (the identity mapping) and C (the permutator) these form a set of primitive, non-interdefinable combinators. Jacobson interprets personal pronouns as the combinator I, and their binding is aided by a complex combinator Z, as in "Mary lost her way". Z is definable using W and B.
Parts of the Formalism
The CCG formalism defines a number of combinators (application, composition, and type-raising being the most common). These operate on syntactically-typed lexical items, by means of Natural deductionNatural deduction
In logic and proof theory, natural deduction is a kind of proof calculus in which logical reasoning is expressed by inference rules closely related to the "natural" way of reasoning...
style proofs. The goal of the proof is to find some way of applying the combinators to a sequence of lexical items until no lexical item is unused in the proof. The resulting type after the proof is complete is the type of the whole expression. Thus, proving that some sequence of words is a sentence of some language amounts to proving that the words reduce to the type S.
Syntactic Types
The syntactic type of a lexical item can be either a primitive type, such as S, N, or NP, or complex, such as S\NP, or NP/N.The complex types, schematizable as X/Y and X\Y, denote functor types that take an argument of type Y and return an object of type X. A forward slash denotes that the argument should appear to the right, while a backslash denotes that the argument should appear on the left. Any type can stand in for the X and Y here, making syntactic types in CCG a recursive type system.
Application Combinators
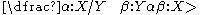
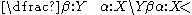
The application combinators, often denoted by > for forward application and < for backward application, apply a lexical item with a functor type to an argument with an appropriate type. The definition of application is given as:Composition Combinators
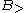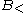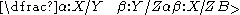
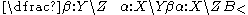
The composition combinators, often denoted by for forward composition and for backward composition, are similar to function composition from mathematics, and can be defined as follows:Type-raising Combinators
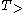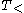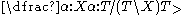
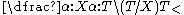
The type-raising combinators, often denoted as for forward type-raising and for backward type-raising, take argument types (usually primitive types) to functor types, which take as their argument the functors that, before type-raising, would have taken them as arguments.Example
The sentence "the dog bit John" has a number of different possible proofs. Below are a few of them. The variety of proofs demonstrates the fact that in CCG, sentences don't have a single structure, as in other models of grammar.Let the types of these lexical items be
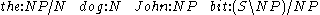
We can perform the simplest proof (changing notation slightly for brevity) as:
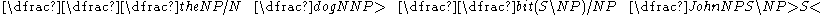
Opting to type-raise and compose some, we could get a fully incremental, left-to-right proof:
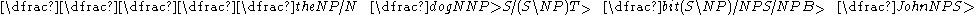
Formal properties
CCGs are known to be able to generate the language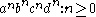. Examples of this are unfortunately too complicated to provide here, but can be found in Vijay-Shanker and Weir (1994).Equivalencies
Vijay-Shanker and Weir (1994) demonstrates that Linear Indexed Grammars, Combinatory Categorial Grammars, Tree-adjoining GrammarsTree-adjoining grammar
Tree-adjoining grammar is a grammar formalism defined by Aravind Joshi. Tree-adjoining grammars are somewhat similar to context-free grammars, but the elementary unit of rewriting is the tree rather than the symbol...
, and Head Grammars
Head grammar
Head Grammar is a grammar formalism introduced in Carl Pollard as an extension of the Context-free grammar class of grammars. The class of head grammars is a subset of the linear context-free rewriting systems....
are weakly equivalent
Weak equivalence
-Mathematics:In mathematics, a weak equivalence is a notion from homotopy theory which in some sense identifies objects that have the same basic "shape"...
formalisms, in that they all define the same string languages.
Further reading
- Michael Moortgat, Categorial Type Logics, Chapter Two in J. van Benthem and A. ter Meulen (eds.) Handbook of Logic and Language. Elsevier, 1997, ISBN 0262220539
External links
- The Combinatory Categorial Grammar Site
- The ACL CCG wiki page (likely to be more up-to-date than this one)