Impossible world
Encyclopedia
In philosophical logic
, the concept of an impossible world (sometimes non-normal world)
is used to model certain
phenomena that cannot be adequately handled using ordinary possible world
s. An
impossible world, w, is the same sort of thing as a possible world (whatever that may be),
except that it is in some sense "impossible." Depending on the context,
this may mean that some contradiction
s are true at w, that the normal laws of logic
or of metaphysics
fail to
hold at w, or both.
in 1965 as a purely technical device to
provide semantics for modal logic
s weaker than the system K — in particular, modal logics that reject
the rule of necessitation:
Such logics are typically referred to as "non-normal." Under the standard interpretation of modal vocabulary in Kripke semantics
, we have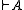
if and only if in each model, 
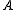holds in all worlds. To construct a model in which 
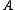holds in all worlds but 
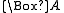does not, we need either to interpret 
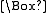in a non-standard manner (that is, we do not just consider the truth of 
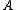in every accessible world), or we reinterpret the condition for being valid. This latter choice is what Kripke does. We single out a class of worlds as normal, and we take validity to be truth in every normal world in a model. in this way we may construct a model in which 
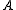is true in every normal world, but in which 
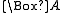is not. We need only ensure that this world (at which 
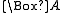fails) have an accessible world which is not normal. Here, 
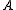can fail, and hence, at our original world, 
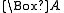fails to be necessary, despite being a truth of the logic.
These non-normal worlds are impossible in the sense that they are not constrained by what is true according to the logic. From the fact that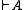
, it does not follow that 
holds in a non-normal world.
For more discussion of the interpretation of the language of modal logic in models with worlds, see the entries on modal logic
and on Kripke semantics
.
is a serious problem for logicians who are interested in developing formal languages
that are "semantically closed" (i.e. that can express their own semantics). The paradox relies on
the seemingly obvious principle of contraction
:
.
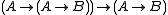There are ways of utilizing non-normal worlds in a semantical system that invalidate contraction. Moreover,
these methods can be given a reasonable philosophical justification by construing non-normal
worlds as worlds at which "the laws of logic fail."
whose antecedent is not merely false, but necessarily so (or whose consequent is necessarily true).
For the sake of argument, assume that either (or both) of the following are the case:
Presumably each of these statements is such that if it is true (false), then it is necessarily true (false).
Thus one (or both) of the following is being assumed:
Now consider the following:
This is intuitively false, as one of the fundamental tenets of intuitionism is precisely that the LEM does not hold. Suppose this statement is cashed out as:
middle holds.
This holds vacuously, given either (1') or (2').
Now suppose impossible worlds are considered in addition to possible ones. It is
compatible with (1') that there are impossible worlds at which intuitionism is true, and with
(2') that there are impossible worlds at which the LEM is false. This yields the interpretation:
middle holds.
This does not seem to be the case, for intuitively there are impossible worlds at which intuitionism is true and the law of excluded middle does not hold.
Philosophical logic
Philosophical logic is a term introduced by Bertrand Russell to represent his idea that the workings of natural language and thought can only be adequately represented by an artificial language; essentially it was his formalization program for the natural language...
, the concept of an impossible world (sometimes non-normal world)
is used to model certain
phenomena that cannot be adequately handled using ordinary possible world
Possible world
In philosophy and logic, the concept of a possible world is used to express modal claims. The concept of possible worlds is common in contemporary philosophical discourse and has also been disputed.- Possibility, necessity, and contingency :...
s. An
impossible world, w, is the same sort of thing as a possible world (whatever that may be),
except that it is in some sense "impossible." Depending on the context,
this may mean that some contradiction
Contradiction
In classical logic, a contradiction consists of a logical incompatibility between two or more propositions. It occurs when the propositions, taken together, yield two conclusions which form the logical, usually opposite inversions of each other...
s are true at w, that the normal laws of logic
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
or of metaphysics
Metaphysics
Metaphysics is a branch of philosophy concerned with explaining the fundamental nature of being and the world, although the term is not easily defined. Traditionally, metaphysics attempts to answer two basic questions in the broadest possible terms:...
fail to
hold at w, or both.
Non-normal modal logics
Non-normal worlds were introduced by Saul KripkeSaul Kripke
Saul Aaron Kripke is an American philosopher and logician. He is a professor emeritus at Princeton and teaches as a Distinguished Professor of Philosophy at the CUNY Graduate Center...
in 1965 as a purely technical device to
provide semantics for modal logic
Modal logic
Modal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
s weaker than the system K — in particular, modal logics that reject
the rule of necessitation:
-
.
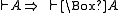Such logics are typically referred to as "non-normal." Under the standard interpretation of modal vocabulary in Kripke semantics
Kripke semantics
Kripke semantics is a formal semantics for non-classical logic systems created in the late 1950s and early 1960s by Saul Kripke. It was first made for modal logics, and later adapted to intuitionistic logic and other non-classical systems...
, we have
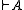if and only if in each model, 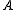holds in all worlds. To construct a model in which 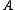holds in all worlds but 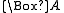does not, we need either to interpret 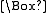in a non-standard manner (that is, we do not just consider the truth of 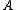in every accessible world), or we reinterpret the condition for being valid. This latter choice is what Kripke does. We single out a class of worlds as normal, and we take validity to be truth in every normal world in a model. in this way we may construct a model in which 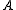is true in every normal world, but in which 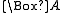is not. We need only ensure that this world (at which 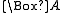fails) have an accessible world which is not normal. Here, 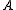can fail, and hence, at our original world, 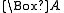fails to be necessary, despite being a truth of the logic.These non-normal worlds are impossible in the sense that they are not constrained by what is true according to the logic. From the fact that
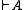, it does not follow that holds in a non-normal world.For more discussion of the interpretation of the language of modal logic in models with worlds, see the entries on modal logic
Modal logic
Modal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
and on Kripke semantics
Kripke semantics
Kripke semantics is a formal semantics for non-classical logic systems created in the late 1950s and early 1960s by Saul Kripke. It was first made for modal logics, and later adapted to intuitionistic logic and other non-classical systems...
.
Avoiding Curry's Paradox
Curry's ParadoxCurry's paradox
Curry's paradox is a paradox that occurs in naive set theory or naive logics, and allows the derivation of an arbitrary sentence from a self-referring sentence and some apparently innocuous logical deduction rules...
is a serious problem for logicians who are interested in developing formal languages
that are "semantically closed" (i.e. that can express their own semantics). The paradox relies on
the seemingly obvious principle of contraction
Idempotency of entailment
Idempotency of entailment is a property of logical systems that states that one may derive the same consequences from many instances of a hypothesis as from just one...
:
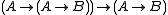.There are ways of utilizing non-normal worlds in a semantical system that invalidate contraction. Moreover,
these methods can be given a reasonable philosophical justification by construing non-normal
worlds as worlds at which "the laws of logic fail."
Counternecessary statements
A counternecessary statement is a counterfactual conditionalCounterfactual conditional
A counterfactual conditional, subjunctive conditional, or remote conditional, abbreviated , is a conditional statement indicating what would be the case if its antecedent were true...
whose antecedent is not merely false, but necessarily so (or whose consequent is necessarily true).
For the sake of argument, assume that either (or both) of the following are the case:
- 1. IntuitionismIntuitionismIn the philosophy of mathematics, intuitionism, or neointuitionism , is an approach to mathematics as the constructive mental activity of humans. That is, mathematics does not consist of analytic activities wherein deep properties of existence are revealed and applied...
is false. - 2. The law of excluded middleLaw of excluded middleIn logic, the law of excluded middle is the third of the so-called three classic laws of thought. It states that for any proposition, either that proposition is true, or its negation is....
is true.
Presumably each of these statements is such that if it is true (false), then it is necessarily true (false).
Thus one (or both) of the following is being assumed:
- 1'. Intuitionism is false at every possible world.
- 2'. The law of excluded middle is true at every possible world.
Now consider the following:
- 3. If intuitionism is true, then the law of excluded middle holds.
This is intuitively false, as one of the fundamental tenets of intuitionism is precisely that the LEM does not hold. Suppose this statement is cashed out as:
- 3'. Every possible world at which intuitionism is true is a possible world at which the law of excluded
middle holds.
This holds vacuously, given either (1') or (2').
Now suppose impossible worlds are considered in addition to possible ones. It is
compatible with (1') that there are impossible worlds at which intuitionism is true, and with
(2') that there are impossible worlds at which the LEM is false. This yields the interpretation:
- 3*. Every (possible or impossible) world at which intuitionism is true is a (possible or impossible) world at which the law of excluded
middle holds.
This does not seem to be the case, for intuitively there are impossible worlds at which intuitionism is true and the law of excluded middle does not hold.
Resources
- Kripke, Saul. 1965. Semantical analysis of modal logic, II: non-normal modal propositional calculi. In J.W. Addison, L. Henkin, and A. Tarski, eds., The Theory of Models. Amsterdam: North Holland.
- Priest, GrahamGraham PriestGraham Priest is Boyce Gibson Professor of Philosophy at the University of Melbourne and Distinguished Professor of Philosophy at the CUNY Graduate Center, as well as a regular visitor at St. Andrews University. Priest is a fellow in residence at Ormond College. He was educated at the University...
(ed.). 1997. Notre Dame Journal of Formal Logic 38, no. 4. (Special issue on impossible worlds.) Table of contents - Priest, Graham. 2001. An Introduction to Non-Classical Logic. Cambridge: Cambridge University Press.
External links
- Edward N. ZaltaEdward N. ZaltaEdward N. Zalta is a Senior research scholar at the Center for the Study of Language and Information. He received his Ph.D. in philosophy from the University of Massachusetts - Amherst in 1980. Zalta has taught courses at Stanford University, Rice University, the University of Salzburg, and the...
, A classically-based theory of impossible worlds (PDF)