Hückel method
Encyclopedia
The Hückel method or Hückel molecular orbital method (HMO) proposed by Erich Hückel
in 1930, is a very simple linear combination of atomic orbitals molecular orbitals (LCAO MO) method for the determination of energies of molecular orbital
s of pi electrons in conjugated hydrocarbon systems, such as ethene, benzene
and butadiene. It is the theoretical basis for the Hückel's rule
; the extended Hückel method
developed by Roald Hoffmann
is the basis of the Woodward-Hoffmann rules
. It was later extended to conjugated molecules such as pyridine
, pyrrole
and furan
that contain atoms other than carbon, known in this context as heteroatoms.
It is a very powerful educational tool and details appear in many chemistry textbooks.
The theory predicts two energy levels for ethylene
with its two pi electrons filling the low-energy HOMO
and the high energy LUMO
remaining empty. In butadiene the 4 pi electrons occupy 2 low energy MO's out of a total of 4 and for benzene
6 energy levels are predicted two of them degenerate
.
For linear and cyclic systems (with n atoms), general solutions exist:
Linear:
Cyclic: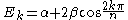
Many predictions have been experimentally verified:
with a few further assumptions concerning the overlap matrix S and the Hamiltonian matrix H.
It is assumed that the overlap matrix S is the identity matrix. This means that overlap between the orbitals is neglected and the orbitals are considered orthogonal. Then the generalised eigenvalue problem of the Ritz method turns into an eigenvalue problem.
The Hamiltonian matrix H = (Hij) is parametrised in the following way:
Hii = α for C atoms and α + hA β for other atoms A.
Hij = β if the two atoms are next to each other and both C, and kAB β for other neighbouring atoms A and B.
Hij = 0 in any other case
The orbitals are the eigenvectors and the energies are the eigenvalues of the Hamiltonian matrix. If the substance is a pure hydrocarbon the problem can be solved without any knowledge about the parameters. For heteroatom systems, such as pyridine, values of hA and kAB have to be specified.
, the molecular orbital
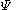is a linear combination of the 2p atomic orbital
s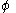
at carbon with their ratios 
:
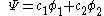
This equation is substituted in the Schrödinger equation
:
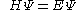
with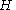
the Hamiltonian
and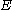
the energy corresponding to the molecular orbital
to give:
This equation is multiplied by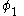
and integrated
to give the equation:
The same equation is multiplied by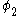
and integrated to give the equation:
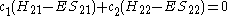
This really can be represented as a matrix
. After converting this set to matrix
notation
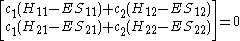
Or more simply as a product of matrices.
where:
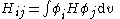
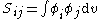
All diagonal Hamiltonian integrals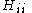
are called coulomb integrals and those of type 
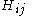, where atoms i and j are connected, are called resonance integrals. The Hückel method assumes that all overlap integrals equal the Kronecker delta, 
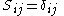, and all nonzero resonance integrals are equal. Resonance integral 
is nonzero when the atoms i and j are bonded.
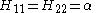
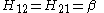
Other assumptions are that the overlap integral between the two atomic orbitals is 0
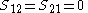
leading to these two homogeneous equation
s:
dividing by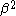
:
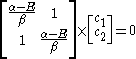
Substituting
for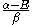 
:
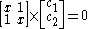
This is convenient for computation, but it is also convenient as the energy and coefficients can be easily found:
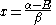
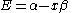
the trivial
solution gives both wavefunction coefficients c equal to zero which is not useful so the other (non-trivial) solution is :
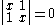
which can be solved by expanding its determinant
:
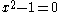
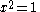
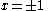
Knowing that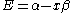
, the energy levels can be found to be:
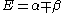
The coefficients can be found by using the previous relationship determined:
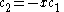
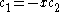
Only one equation is necessary however:
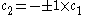
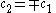
The second constant can be replaced giving the following wave equation.
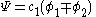
After normalization the coefficient is obtained:
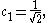
Leaving
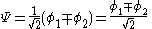
The constant β in the energy term is negative; therefore,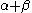
with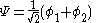 
is the lower energy corresponding to the HOMO
and is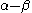
with 
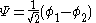the LUMO
energy.
is a linear combination of the 4p 
AO's at carbon with their ratios 
:
The secular equation is:
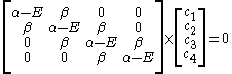
which leads to
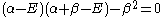
and:
Erich Hückel
Erich Armand Arthur Joseph Hückel was a German physicist and physical chemist. He is known for two major contributions:*The Debye–Hückel theory of electrolytic solutions...
in 1930, is a very simple linear combination of atomic orbitals molecular orbitals (LCAO MO) method for the determination of energies of molecular orbital
Molecular orbital
In chemistry, a molecular orbital is a mathematical function describing the wave-like behavior of an electron in a molecule. This function can be used to calculate chemical and physical properties such as the probability of finding an electron in any specific region. The term "orbital" was first...
s of pi electrons in conjugated hydrocarbon systems, such as ethene, benzene
Benzene
Benzene is an organic chemical compound. It is composed of 6 carbon atoms in a ring, with 1 hydrogen atom attached to each carbon atom, with the molecular formula C6H6....
and butadiene. It is the theoretical basis for the Hückel's rule
Hückel's rule
In organic chemistry, Hückel's rule estimates whether a planar ring molecule will have aromatic properties. The quantum mechanical basis for its formulation was first worked out by physical chemist Erich Hückel in 1931...
; the extended Hückel method
Extended Huckel method
The extended Hückel method is a semiempirical quantum chemistry method, developed by Roald Hoffmann since 1963. It is based on the Hückel method but, while the original Hückel method only considers pi orbitals, the extended method also includes the sigma orbitals.The extended Hückel method can be...
developed by Roald Hoffmann
Roald Hoffmann
Roald Hoffmann is an American theoretical chemist who won the 1981 Nobel Prize in Chemistry. He currently teaches at Cornell University in Ithaca, New York.-Escape from the Holocaust:...
is the basis of the Woodward-Hoffmann rules
Woodward-Hoffmann rules
The Woodward–Hoffmann rules devised by Robert Burns Woodward and Roald Hoffmann are a set of rules in organic chemistry predicting the stereochemistry of pericyclic reactions based on orbital symmetry. These include electrocyclic reactions, cycloadditions , sigmatropic reactions, and group transfer...
. It was later extended to conjugated molecules such as pyridine
Pyridine
Pyridine is a basic heterocyclic organic compound with the chemical formula C5H5N. It is structurally related to benzene, with one C-H group replaced by a nitrogen atom...
, pyrrole
Pyrrole
Pyrrole is a heterocyclic aromatic organic compound, a five-membered ring with the formula C4H4NH. It is a colourless volatile liquid that darkens readily upon exposure to air. Substituted derivatives are also called pyrroles, e.g., N-methylpyrrole, C4H4NCH3...
and furan
Furan
Furan is a heterocyclic organic compound, consisting of a five-membered aromatic ring with four carbon atoms and one oxygen. The class of compounds containing such rings are also referred to as furans....
that contain atoms other than carbon, known in this context as heteroatoms.
It is a very powerful educational tool and details appear in many chemistry textbooks.
Hückel characteristics
The method has several characteristics:- It limits itself to conjugatedConjugated systemIn chemistry, a conjugated system is a system of connected p-orbitals with delocalized electrons in compounds with alternating single and multiple bonds, which in general may lower the overall energy of the molecule and increase stability. Lone pairs, radicals or carbenium ions may be part of the...
hydrocarbons - Only pi electron MO's are included because these determine the general properties of these molecules and the sigma electrons are ignored. This is referred to as sigma-pi separability. It is justified by the orthogonality of sigma and pi orbitals in planar molecules. For this reason, the Hückel method is limited to planar systems.
- The method takes as inputs the LCAO MO Method, the Schrödinger equationSchrödinger equationThe Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
and simplifications based on orbital symmetry considerations. Interestingly the method does not take in any physical constants. - The method predicts how many energy levels exist for a given molecule, which levels are degenerateDegenerate energy levelIn physics, two or more different quantum states are said to be degenerate if they are all at the same energy level. Statistically this means that they are all equally probable of being filled, and in Quantum Mechanics it is represented mathematically by the Hamiltonian for the system having more...
and it expresses the MO energies as the sum of two other energy terms called alpha, the energy of an electron in a 2p-orbital and beta, an interaction energy between two p orbitals which are still unknown but importantly have become independent of the molecule. In addition it enables calculation of charge densityCharge densityThe linear, surface, or volume charge density is the amount of electric charge in a line, surface, or volume, respectively. It is measured in coulombs per meter , square meter , or cubic meter , respectively, and represented by the lowercase Greek letter Rho . Since there are positive as well as...
for each atom in the pi framework, the bond orderBond orderBond order is the number of chemical bonds between a pair of atoms. For example, in diatomic nitrogen N≡N the bond order is 3, while in acetylene H−C≡C−H the bond order between the two carbon atoms is also 3, and the C−H bond order is 1. Bond order gives an indication to the stability of a bond....
between any two atoms and the overall molecular dipole moment.
Hückel results
The results for a few simple molecules are tabulated below:| Molecule | Energy | Frontier orbital | HOMO - LUMO energy gap |
| Ethylene Ethylene Ethylene is a gaseous organic compound with the formula . It is the simplest alkene . Because it contains a carbon-carbon double bond, ethylene is classified as an unsaturated hydrocarbon. Ethylene is widely used in industry and is also a plant hormone... |
E1 = α - β | LUMO | -2β |
| |E2 = α + β | HOMO | ||
| Butadiene | E1 = α + 1.62β | ||
| |E2 = α + 0.62β | HOMO | -1.24β | |
| |E3 = α - 0.62β | LUMO | ||
| |E4 = α - 1.62β | |||
| Benzene Benzene Benzene is an organic chemical compound. It is composed of 6 carbon atoms in a ring, with 1 hydrogen atom attached to each carbon atom, with the molecular formula C6H6.... |
E1 = α + 2β | ||
| |E2 = α + β | |||
| |E3 = α + β | HOMO | -2β | |
| |E4 = α - β | LUMO | ||
| |E5 = α - β | |||
| |E6 = α - 2β | |||
| Cyclobutadiene Cyclobutadiene Cyclobutadiene is the smallest [n]-annulene , an extremely unstable hydrocarbon having a lifetime shorter than five seconds in the free state. It has chemical formula 44 and a rectangular structure verified by infrared studies. This is in contrast to the square geometry predicted by simple Hückel... |
E1 = α + 2β | ||
| |E2 = α | SOMO | 0 | |
| |E3 = α | SOMO | ||
| |E4 = α - 2β | |||
| Table 1. Hückel method results Lowest energies op top α and β are both negative values | |||
The theory predicts two energy levels for ethylene
Ethylene
Ethylene is a gaseous organic compound with the formula . It is the simplest alkene . Because it contains a carbon-carbon double bond, ethylene is classified as an unsaturated hydrocarbon. Ethylene is widely used in industry and is also a plant hormone...
with its two pi electrons filling the low-energy HOMO
Homo
Homo may refer to:*the Greek prefix ὅμο-, meaning "the same"*the Latin for man, human being*Homo, the taxonomical genus including modern humans...
and the high energy LUMO
Lumo
Lumo is a 2007 documentary film about twenty-year-old Lumo Sinai, a woman who fell victim to "Africa's First World War." While returning home one day, Lumo and another woman were gang-raped by a group of soldiers fighting for control of the Democratic Republic of the Congo during the 1994 Rwandan...
remaining empty. In butadiene the 4 pi electrons occupy 2 low energy MO's out of a total of 4 and for benzene
Benzene
Benzene is an organic chemical compound. It is composed of 6 carbon atoms in a ring, with 1 hydrogen atom attached to each carbon atom, with the molecular formula C6H6....
6 energy levels are predicted two of them degenerate
Degenerate energy level
In physics, two or more different quantum states are said to be degenerate if they are all at the same energy level. Statistically this means that they are all equally probable of being filled, and in Quantum Mechanics it is represented mathematically by the Hamiltonian for the system having more...
.
For linear and cyclic systems (with n atoms), general solutions exist:
Linear:
Cyclic:
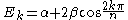
Many predictions have been experimentally verified:
- The HOMO - LUMO gap in terms of the β constant correlates directly with the respective molecular electronic transitionMolecular electronic transitionMolecular electronic transitions take place when electrons in a molecule are excited from one energy level to a higher energy level. The energy change associated with this transition provides information on the structure of a molecule and determines many molecular properties such as color...
s observed with UV/VIS spectroscopy. For linear polyenePolyenePolyenes are poly-unsaturated organic compounds that contain one or more sequences of alternating double and single carbon-carbon bonds. These double carbon-carbon bonds interact in a process known as conjugation, which results in an overall lower energy state of the molecule.Organic compounds with...
s the energy gap is given as: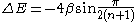
- from which a value for β can be obtained between −60 and −70 kcalCalorieThe calorie is a pre-SI metric unit of energy. It was first defined by Nicolas Clément in 1824 as a unit of heat, entering French and English dictionaries between 1841 and 1867. In most fields its use is archaic, having been replaced by the SI unit of energy, the joule...
/molMole (unit)The mole is a unit of measurement used in chemistry to express amounts of a chemical substance, defined as an amount of a substance that contains as many elementary entities as there are atoms in 12 grams of pure carbon-12 , the isotope of carbon with atomic weight 12. This corresponds to a value...
(−250 to −290 kJ/mol).- The predicted MO energies as stipulated by Koopmans' theoremKoopmans' theoremKoopmans' theorem states that in closed-shell Hartree-Fock theory, the first ionization energy of a molecular system is equal to the negative of the orbital energy of the highest occupied molecular orbital...
correlate with photoelectron spectroscopy. - The Hückel delocalization energy correlates with the experimental heat of combustionHeat of combustionThe heat of combustion is the energy released as heat when a compound undergoes complete combustion with oxygen under standard conditions. The chemical reaction is typically a hydrocarbon reacting with oxygen to form carbon dioxide, water and heat...
. This energy is defined as the difference between the total predicted pi energy (in benzene 8β) and a hypothetical pi energy in which all ethylene units are assumed isolated each contributing 2β (making benzene 3 x 2β = 6β). - Molecules with MO's paired up such that only the sign differs (for example α+/-β) are called alternant hydrocarbons and have in common small molecular dipole moments. This is in contrast to non-alternant hydrocarbons such as azuleneAzuleneAzulene is an organic compound and an isomer of naphthalene. Whereas naphthalene is colourless, azulene is dark blue. Its name is derived from the Spanish word azul, meaning "blue"...
and fulveneFulveneFulvene is one of several hydrocarbons with the same formula as benzene, C6H6. Fulvenes include the derivatives of this simple hydrocarbon, which itself is rarely encountered. Thiele is credited with discovering the scope of the reaction between cyclopentadiene and aldehydes and ketones that...
that have large dipole moments. The Hückel theory is more accurate for alternant hydrocarbons. - For cyclobutadieneCyclobutadieneCyclobutadiene is the smallest [n]-annulene , an extremely unstable hydrocarbon having a lifetime shorter than five seconds in the free state. It has chemical formula 44 and a rectangular structure verified by infrared studies. This is in contrast to the square geometry predicted by simple Hückel...
the theory predicts that the two high-energy electrons occupy a degenerate pair of MO's that are neither stabilized or destabilized. Hence the square molecule would be a very reactive triplet diradicalDiradicalA diradical in organic chemistry is a molecular species with two electrons occupying two degenerate molecular orbitals . They are known by their higher reactivities and shorter lifetimes. In a broader definition diradicals are even-electron molecules that have one bond less than the number...
(the ground state is actually rectangular without degenerate orbitals). In fact, all cyclic conjugated hydrocarbons with a total of 4n pi electrons share this MO pattern and this form the basis of Hückel's ruleHückel's ruleIn organic chemistry, Hückel's rule estimates whether a planar ring molecule will have aromatic properties. The quantum mechanical basis for its formulation was first worked out by physical chemist Erich Hückel in 1931...
.
- The predicted MO energies as stipulated by Koopmans' theorem
Mathematics behind the Hückel method
The Hückel method can be derived from the Ritz methodRitz method
The Ritz method is a direct method to find an approximate solution for boundary value problems. The method is named after Walter Ritz.In quantum mechanics, a system of particles can be described in terms of an "energy functional" or Hamiltonian, which will measure the energy of any proposed...
with a few further assumptions concerning the overlap matrix S and the Hamiltonian matrix H.
It is assumed that the overlap matrix S is the identity matrix. This means that overlap between the orbitals is neglected and the orbitals are considered orthogonal. Then the generalised eigenvalue problem of the Ritz method turns into an eigenvalue problem.
The Hamiltonian matrix H = (Hij) is parametrised in the following way:
Hii = α for C atoms and α + hA β for other atoms A.
Hij = β if the two atoms are next to each other and both C, and kAB β for other neighbouring atoms A and B.
Hij = 0 in any other case
The orbitals are the eigenvectors and the energies are the eigenvalues of the Hamiltonian matrix. If the substance is a pure hydrocarbon the problem can be solved without any knowledge about the parameters. For heteroatom systems, such as pyridine, values of hA and kAB have to be specified.
Hückel solution for ethylene
In the Hückel treatment for ethyleneEthylene
Ethylene is a gaseous organic compound with the formula . It is the simplest alkene . Because it contains a carbon-carbon double bond, ethylene is classified as an unsaturated hydrocarbon. Ethylene is widely used in industry and is also a plant hormone...
, the molecular orbital
Molecular orbital
In chemistry, a molecular orbital is a mathematical function describing the wave-like behavior of an electron in a molecule. This function can be used to calculate chemical and physical properties such as the probability of finding an electron in any specific region. The term "orbital" was first...
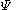is a linear combination of the 2p atomic orbitalAtomic orbital
An atomic orbital is a mathematical function that describes the wave-like behavior of either one electron or a pair of electrons in an atom. This function can be used to calculate the probability of finding any electron of an atom in any specific region around the atom's nucleus...
s
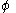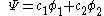
at carbon with their ratios :This equation is substituted in the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
:
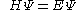
with
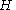the HamiltonianHamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
and
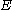the energy corresponding to the molecular orbitalto give:
This equation is multiplied by
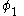and integratedIntegral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
to give the equation:
The same equation is multiplied by
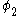and integrated to give the equation: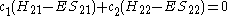This really can be represented as a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
. After converting this set to matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
notation
Or more simply as a product of matrices.
where:
All diagonal Hamiltonian integrals
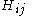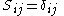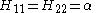
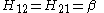
are called coulomb integrals and those of type , where atoms i and j are connected, are called resonance integrals. The Hückel method assumes that all overlap integrals equal the Kronecker delta, , and all nonzero resonance integrals are equal. Resonance integral is nonzero when the atoms i and j are bonded.Other assumptions are that the overlap integral between the two atomic orbitals is 0
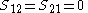
leading to these two homogeneous equation
Homogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
s:
dividing by
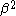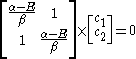
:Substituting
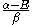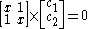
for :This is convenient for computation, but it is also convenient as the energy and coefficients can be easily found:
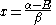
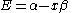
the trivial
Trivial (mathematics)
In mathematics, the adjective trivial is frequently used for objects that have a very simple structure...
solution gives both wavefunction coefficients c equal to zero which is not useful so the other (non-trivial) solution is :
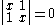
which can be solved by expanding its determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
:
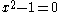
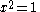
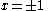
Knowing that
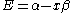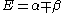
, the energy levels can be found to be:The coefficients can be found by using the previous relationship determined:
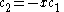
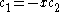
Only one equation is necessary however:
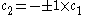
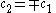
The second constant can be replaced giving the following wave equation.
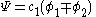
After normalization the coefficient is obtained:
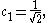
Leaving
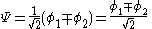
The constant β in the energy term is negative; therefore,
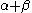with 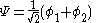is the lower energy corresponding to the HOMOHomo
Homo may refer to:*the Greek prefix ὅμο-, meaning "the same"*the Latin for man, human being*Homo, the taxonomical genus including modern humans...
and is
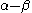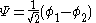with the LUMOLumo
Lumo is a 2007 documentary film about twenty-year-old Lumo Sinai, a woman who fell victim to "Africa's First World War." While returning home one day, Lumo and another woman were gang-raped by a group of soldiers fighting for control of the Democratic Republic of the Congo during the 1994 Rwandan...
energy.
Hückel solution for butadiene
In the Hückel treatment for butadiene, the MO is a linear combination of the 4p AO's at carbon with their ratios :The secular equation is:
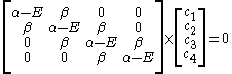
which leads to
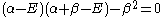
and:
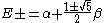
External links
- Hückel method @ chem.swin.edu.au Link
Further reading
- The HMO-Model and its applications: Basis and Manipulation, E. Heilbronner and H. Bock, English translation, 1976, Verlag Chemie.
- The HMO-Model and its applications: Problems with Solutions, E. Heilbronner and H. Bock, English translation, 1976, Verlag Chemie.
- The HMO-Model and its applications: Tables of Hückel Molecular Orbitals , E. Heilbronner and H. Bock, English translation, 1976, Verlag Chemie.