
Huber Loss Function
Encyclopedia
In statistical theory
, the Huber loss function is a function used in robust estimation
that allows construction of an estimate which allows the effect of outliers to be reduced, while treating non-outliers in a more standard way.
. Huber (1964) defines the loss function piecewise by

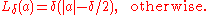
This function is quadratic for small values of a, and linear for large values, with equal values and slopes of the different sections at the two points where |a| = δ. In use, the variable often refers to the residuals, that is to the difference between the observed and predicted values, i.e.
often refers to the residuals, that is to the difference between the observed and predicted values, i.e. 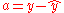 .
.
 of the parameter space
of the parameter space
):
Two very commonly-used loss functions are the squared loss
,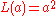 , and the absolute loss
, and the absolute loss
, . While the absolute loss is not differentiable at exactly one point,
. While the absolute loss is not differentiable at exactly one point,  , where it is subdifferentiable with its convex
, where it is subdifferentiable with its convex
subdifferential equal to the interval ; the absolute-value loss function results in a median-unbiased estimator, which can be evaluated for particular data sets by linear programming
; the absolute-value loss function results in a median-unbiased estimator, which can be evaluated for particular data sets by linear programming
. The squared loss has the disadvantage that it has the tendency to be dominated by outliers---when summing over a set of 's (as in
's (as in 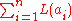 ), the sample mean is influenced too much by a few particularly-large a-values when the distribution is heavy tailed: in terms of estimation theory
), the sample mean is influenced too much by a few particularly-large a-values when the distribution is heavy tailed: in terms of estimation theory
, the asymptotic relative efficiency of the mean is poor for heavy-tailed distributions
As defined above, the Huber loss function is convex
in a uniform neighborhood of its minimum , at the boundary of this uniform neighborhood, the Huber loss function has a differentiable extension to an affine function at points
, at the boundary of this uniform neighborhood, the Huber loss function has a differentiable extension to an affine function at points 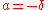 and
and  . These properties allow it to combine much of the sensitivity of the mean-unbiased, minimum-variance estimator of the mean (using the quadratic loss function) and the robustness of the median-unbiased estimor (using the absolute value function).
. These properties allow it to combine much of the sensitivity of the mean-unbiased, minimum-variance estimator of the mean (using the quadratic loss function) and the robustness of the median-unbiased estimor (using the absolute value function).
The log cosh loss function, which is defined as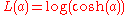 has a behavior like that of the Huber loss function.
has a behavior like that of the Huber loss function.
Statistical theory
The theory of statistics provides a basis for the whole range of techniques, in both study design and data analysis, that are used within applications of statistics. The theory covers approaches to statistical-decision problems and to statistical inference, and the actions and deductions that...
, the Huber loss function is a function used in robust estimation
Robust statistics
Robust statistics provides an alternative approach to classical statistical methods. The motivation is to produce estimators that are not unduly affected by small departures from model assumptions.- Introduction :...
that allows construction of an estimate which allows the effect of outliers to be reduced, while treating non-outliers in a more standard way.
Definition
The Huber loss function describes the penalty incurred by an estimation procedureEstimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
. Huber (1964) defines the loss function piecewise by

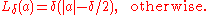
This function is quadratic for small values of a, and linear for large values, with equal values and slopes of the different sections at the two points where |a| = δ. In use, the variable
 often refers to the residuals, that is to the difference between the observed and predicted values, i.e.
often refers to the residuals, that is to the difference between the observed and predicted values, i.e. 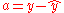 .
.Motivation
For estimating parameters, it is desirable for a loss function to have the following properties (for all values of of the parameter space
of the parameter spaceParameter space
In science, a parameter space is the set of values of parameters encountered in a particular mathematical model. Often the parameters are inputs of a function, in which case the technical term for the parameter space is domain of a function....
):
- It is greater than or equal to the 0-1 loss function0-1 loss functionIn statistics and decision theory, a frequently used loss function is the 0-1 loss functionwhere I is the indicator notation....
(which is defined as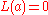 if
if  and
and 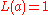 otherwise).
otherwise). - It is continuous (or lower semicontinuous).
Two very commonly-used loss functions are the squared loss
Mean squared error
In statistics, the mean squared error of an estimator is one of many ways to quantify the difference between values implied by a kernel density estimator and the true values of the quantity being estimated. MSE is a risk function, corresponding to the expected value of the squared error loss or...
,
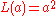 , and the absolute loss
, and the absolute lossAbsolute deviation
In statistics, the absolute deviation of an element of a data set is the absolute difference between that element and a given point. Typically the point from which the deviation is measured is a measure of central tendency, most often the median or sometimes the mean of the data set.D_i = |x_i-m|...
,
 . While the absolute loss is not differentiable at exactly one point,
. While the absolute loss is not differentiable at exactly one point,  , where it is subdifferentiable with its convex
, where it is subdifferentiable with its convexConvex analysis
Convex analysis is the branch of mathematics devoted to the study of properties of convex functions and convex sets, often with applications in convex minimization, a subdomain of optimization theory....
subdifferential equal to the interval
 ; the absolute-value loss function results in a median-unbiased estimator, which can be evaluated for particular data sets by linear programming
; the absolute-value loss function results in a median-unbiased estimator, which can be evaluated for particular data sets by linear programmingLinear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
. The squared loss has the disadvantage that it has the tendency to be dominated by outliers---when summing over a set of
 's (as in
's (as in 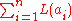 ), the sample mean is influenced too much by a few particularly-large a-values when the distribution is heavy tailed: in terms of estimation theory
), the sample mean is influenced too much by a few particularly-large a-values when the distribution is heavy tailed: in terms of estimation theoryEstimation theory
Estimation theory is a branch of statistics and signal processing that deals with estimating the values of parameters based on measured/empirical data that has a random component. The parameters describe an underlying physical setting in such a way that their value affects the distribution of the...
, the asymptotic relative efficiency of the mean is poor for heavy-tailed distributions
As defined above, the Huber loss function is convex
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
in a uniform neighborhood of its minimum
 , at the boundary of this uniform neighborhood, the Huber loss function has a differentiable extension to an affine function at points
, at the boundary of this uniform neighborhood, the Huber loss function has a differentiable extension to an affine function at points 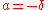 and
and  . These properties allow it to combine much of the sensitivity of the mean-unbiased, minimum-variance estimator of the mean (using the quadratic loss function) and the robustness of the median-unbiased estimor (using the absolute value function).
. These properties allow it to combine much of the sensitivity of the mean-unbiased, minimum-variance estimator of the mean (using the quadratic loss function) and the robustness of the median-unbiased estimor (using the absolute value function).The log cosh loss function, which is defined as
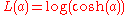 has a behavior like that of the Huber loss function.
has a behavior like that of the Huber loss function.See also
- Robust regressionRobust regressionIn robust statistics, robust regression is a form of regression analysis designed to circumvent some limitations of traditional parametric and non-parametric methods. Regression analysis seeks to find the effect of one or more independent variables upon a dependent variable...
- M-estimatorM-estimatorIn statistics, M-estimators are a broad class of estimators, which are obtained as the minima of sums of functions of the data. Least-squares estimators and many maximum-likelihood estimators are M-estimators. The definition of M-estimators was motivated by robust statistics, which contributed new...
- Visual comparison of different M-estimators

