Holonomic constraints
Encyclopedia
In a system of point particle
s, holonomic constraints are relations between the coordinates and (possibly) time which can be expressed in the following form:
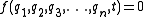, where 
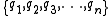, are the n coordinates which describe the system. Holonomic constraints are rigid. For example, the motion of a particle constrained to lie on the surface of a sphere
is subject to a holonomic constraint, but if the particle is able to fall off the sphere under the influence of gravity, the constraint becomes non-holonomic.
Velocity-dependent constraints such as
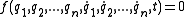
can be holonomic if they can be integrated into a simple holonomic constraint.
Use in Molecular Dynamics
Holonomic constraints are used in classical molecular dynamics simulations of molecules to restrict the motions of hydrogen
s attached to heavy atoms. These simulations use numerical methods to integrate the equations of motion of the molecular system. The numerical stability
of the methods used determines how small the timestep
of the integration must be in order to provide an accurate result. The fastest vibrating oscillators have the greatest effect on the timestep, but since these oscillators usually only represent bonds between hydrogen and heavier atoms, they are of little chemical interest. Imposing a holonomic constraint on heavy atom-hydrogen bonds makes the integration methods much more stable, at the relatively small cost of discarding uninteresting motions.
Point particle
A point particle is an idealization of particles heavily used in physics. Its defining feature is that it lacks spatial extension: being zero-dimensional, it does not take up space...
s, holonomic constraints are relations between the coordinates and (possibly) time which can be expressed in the following form:
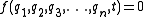, where 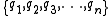, are the n coordinates which describe the system. Holonomic constraints are rigid. For example, the motion of a particle constrained to lie on the surface of a sphereSphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
is subject to a holonomic constraint, but if the particle is able to fall off the sphere under the influence of gravity, the constraint becomes non-holonomic.
Velocity-dependent constraints such as
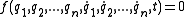
can be holonomic if they can be integrated into a simple holonomic constraint.
Use in Molecular DynamicsMolecular dynamicsMolecular dynamics is a computer simulation of physical movements of atoms and molecules. The atoms and molecules are allowed to interact for a period of time, giving a view of the motion of the atoms...
Simulations
Holonomic constraints are used in classical molecular dynamics simulations of molecules to restrict the motions of hydrogenHydrogen
Hydrogen is the chemical element with atomic number 1. It is represented by the symbol H. With an average atomic weight of , hydrogen is the lightest and most abundant chemical element, constituting roughly 75% of the Universe's chemical elemental mass. Stars in the main sequence are mainly...
s attached to heavy atoms. These simulations use numerical methods to integrate the equations of motion of the molecular system. The numerical stability
Numerical stability
In the mathematical subfield of numerical analysis, numerical stability is a desirable property of numerical algorithms. The precise definition of stability depends on the context, but it is related to the accuracy of the algorithm....
of the methods used determines how small the timestep
Numerical ordinary differential equations
Numerical ordinary differential equations is the part of numerical analysis which studies the numerical solution of ordinary differential equations...
of the integration must be in order to provide an accurate result. The fastest vibrating oscillators have the greatest effect on the timestep, but since these oscillators usually only represent bonds between hydrogen and heavier atoms, they are of little chemical interest. Imposing a holonomic constraint on heavy atom-hydrogen bonds makes the integration methods much more stable, at the relatively small cost of discarding uninteresting motions.