Hilbert's Theorem 90
Encyclopedia
In abstract algebra
, Hilbert's Theorem 90 (or Satz 90) refers to an important result on cyclic extensions of field
s (or to one of its generalizations) that leads to Kummer theory
. In its most basic form, it tells us that if L/K is a cyclic extension of fields with Galois group G =Gal(L/K)
generated by an element s and if a is an element of L of relative norm 1, then there exists b in L such that
The theorem takes its name from the fact that it is the 90th theorem in David Hilbert
's famous Zahlbericht
, although it is originally due to . Often a more general theorem due to is given the name, stating that if L/K is a finite Galois extension of fields with Galois group G =Gal(L/K), then the first cohomology group is trivial:
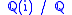. The Galois group is cyclic of order 2, its generator s is acting via conjugation: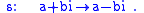
An element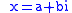
in L has norm 
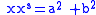. An element of norm one corresponds to a rational solution of the equation a2 +b2=1 or in other words, a point with rational coordinates on the unit circle
. Hilbert's Theorem 90 then states that every element y of norm one can be parametrized (with integral c,d) as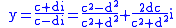
which may be viewed as a rational parametrization of the rational points on the unit circle. Rational points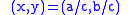
on the unit circle 
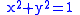correspond to Pythagorean triple
s, i.e. triples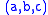
of integers satisfying 
.
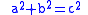: if L× is the multiplicative group
of any (not necessarily finite) Galois extension L of a field K with corresponding Galois group G, then
A further generalization using non-abelian group cohomology states that if H is either the general
or special linear group
over L, then
This is a generalization since L× = GL1(L).
Another generalization is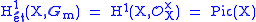
for X a scheme, and another one to Milnor K-theory
plays a role in Voevodsky's
proof of the Milnor conjecture
.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, Hilbert's Theorem 90 (or Satz 90) refers to an important result on cyclic extensions of field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
s (or to one of its generalizations) that leads to Kummer theory
Kummer theory
In abstract algebra and number theory, Kummer theory provides a description of certain types of field extensions involving the adjunction of nth roots of elements of the base field. The theory was originally developed by Ernst Eduard Kummer around the 1840s in his pioneering work on Fermat's last...
. In its most basic form, it tells us that if L/K is a cyclic extension of fields with Galois group G =Gal(L/K)
generated by an element s and if a is an element of L of relative norm 1, then there exists b in L such that
- a = s(b)/b.
The theorem takes its name from the fact that it is the 90th theorem in David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
's famous Zahlbericht
Zahlbericht
In mathematics, the Zahlbericht was a report on algebraic number theory by .-History: and and the English introduction to give detailed discussions of the history and influence of Hilbert's Zahlbericht....
, although it is originally due to . Often a more general theorem due to is given the name, stating that if L/K is a finite Galois extension of fields with Galois group G =Gal(L/K), then the first cohomology group is trivial:
- H1(G, L×) = {1}
Examples
Let L/K be the quadratic extension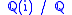. The Galois group is cyclic of order 2, its generator s is acting via conjugation: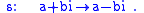An element
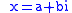in L has norm 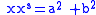. An element of norm one corresponds to a rational solution of the equation a2 +b2=1 or in other words, a point with rational coordinates on the unit circleUnit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
. Hilbert's Theorem 90 then states that every element y of norm one can be parametrized (with integral c,d) as
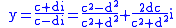
which may be viewed as a rational parametrization of the rational points on the unit circle. Rational points
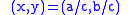on the unit circle 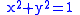correspond to Pythagorean triplePythagorean triple
A Pythagorean triple consists of three positive integers a, b, and c, such that . Such a triple is commonly written , and a well-known example is . If is a Pythagorean triple, then so is for any positive integer k. A primitive Pythagorean triple is one in which a, b and c are pairwise coprime...
s, i.e. triples
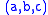of integers satisfying 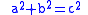.Cohomology
The theorem can be stated in terms of group cohomologyGroup cohomology
In abstract algebra, homological algebra, algebraic topology and algebraic number theory, as well as in applications to group theory proper, group cohomology is a way to study groups using a sequence of functors H n. The study of fixed points of groups acting on modules and quotient modules...
: if L× is the multiplicative group
Multiplicative group
In mathematics and group theory the term multiplicative group refers to one of the following concepts, depending on the context*any group \scriptstyle\mathfrak \,\! whose binary operation is written in multiplicative notation ,*the underlying group under multiplication of the invertible elements of...
of any (not necessarily finite) Galois extension L of a field K with corresponding Galois group G, then
- H1(G, L×) = {1}.
A further generalization using non-abelian group cohomology states that if H is either the general
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
or special linear group
Special linear group
In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
over L, then
- H1(G,H) = {1}.
This is a generalization since L× = GL1(L).
Another generalization is
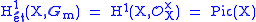for X a scheme, and another one to Milnor K-theoryMilnor K-theory
In mathematics, Milnor K-theory was an early attempt to define higher algebraic K-theory, introduced by .The calculation of K2 of a field k led Milnor to the following ad hoc definition of "higher" K-groups by...
plays a role in Voevodsky's
Vladimir Voevodsky
Vladimir Voevodsky is a Russian American mathematician. His work in developing a homotopy theory for algebraic varieties and formulating motivic cohomology led to the award of a Fields Medal in 2002.- Biography :...
proof of the Milnor conjecture
Milnor conjecture
In mathematics, the Milnor conjecture was a proposal by of a description of the Milnor K-theory of a general field F with characteristic different from 2, by means of the Galois cohomology of F with coefficients in Z/2Z. It was proved by .-Statement of the theorem:Let F be a field of...
.