Highly structured ring spectrum
Encyclopedia
In mathematics, a highly structured ring spectrum or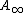 
-ring is an object in homotopy theory encoding a refinement of a multiplicative structure on a cohomology theory. A commutative version of an 
-ring is called an 
-ring. While originally motivated by questions of geometric topology
and bundle theory, they are today most often used in stable homotopy theory
.
, and which has allowed also new constructions of more classical objects such as Morava K-theory
. Beside their formal properties,
-structures are also important in calculations, since they allow for operations in the underlying cohomology theory, analogous to (and generalizing) the well-known Steenrod operations
in ordinary cohomology. As not every cohomology theory allows such operations, not every multiplicative structure may be refined to an
-structure and even in cases where this is possible, it may be a formidable task to prove that.
The rough idea of highly structured ring spectra is the following: If multiplication in a cohomology theory (analogous to the multiplication in singular cohomology, inducing the cup product
) fulfills associativity (and commutativity) only up to homotopy, this is too lax for many constructions (e.g. for limits and colimits in the sense of category theory
). On the other hand, requiring strict associativity (or commutativity) in a naive way is too restrictive for many of the wanted examples. A basic idea is that the relations need only hold up to homotopy, but these homotopies should fulfill again some homotopy relations, whose homotopies again fulfill some further homotopy conditions; and so on. The classical approach organizes this structure via operads, while the recent approach of Jacob Lurie
deals with it in the language of
-categories. The most widely used approaches today employ the language of model categories
.
All these approaches depend on building carefully an underlying category of Spectra
.
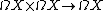
by composition of loops. Here the two loops are sped up by a factor of 2 and the first takes the interval [0,1/2] and the second [1/2,1]. This product is not associative since the scalings are not compatible, but it is associative up to homotopy and the homotopies are coherent up to higher homotopies and so on. This situation can be made precise by saying that ΩX is an algebra over the little interval operad. This is an example of an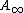
-operad, i.e. an operad of topological spaces which is homotopy equivalent to the associative operad. An 
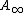-ring spectrum can now be imagined as an algebra over an 
-operad in a suitable category of spectra and suitable compatibility conditions (see May, 1977).
For the definition of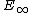
-ring spectra essentially the same approach works, where one replaces the 
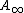-operad by an 
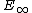-operad, i.e. an operad of contractible topological spaces. An example of such an operad can be again motivated by the study of loop spaces. The product of the double loop space 
is already commutative up to homotopy, but this homotopy fulfills no higher conditions. To get full coherence of higher homotopies one has to pass to the infinite loop space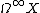 
. This leads to the in 
-cube operad of infinite-dimensional cubes in infinite-dimensional space, which is an example of an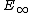 
-operad.
The above approach was pioneered by J. Peter May
. Together with Elmendorf, Kriz and Mandell he developed in the 90s a variant of his older definition of spectra, so called S-modules (see Elmendorf et al, 2007). S-modules possess a model structure, whose homotopy category is the stable homotopy category. In S-modules the category of modules over an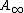
-operad and the category of monoids
are Quillen equivalent
and likewise the category of modules over an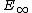
-operad and the category of commutative monoids. Therefore is it possible to define 
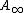-ring spectra and 
-ring spectra as (commutative) monoids in the category of S-modules, so called (commutative) S-algebras. Since (commutative) monoids are easier to deal with than algebras over complicated operads, this new approach is for many purposes more convenient. It should, however, be noted that the actual construction of the category of S-modules is technically quite complicated.
In the most naive sense, a spectrum is a sequence of (pointed) spaces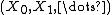
together with maps 
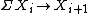, where ΣX denotes the suspension. Another viewpoint is the following: one considers the category of sequences of spaces together with the monoidal
structure given by a smash product
. Then the sphere sequence
has the structure of a monoid and spectra are just modules over this monoid. If this monoid was commutative, then a monoidal structure on the category of modules over it would arise (as in algebra
the modules over a commutative ring have a tensor product). But the monoid structure of the sphere sequence is not commutative due to different orderings of the coordinates.
The idea is now that one can build the coordinate changes into the definition of a sequence: a symmetric sequence is a sequence of spaces
together with an action of the n-th symmetric group
on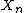
. If one equips this with a suitable monoidal product, one gets that the sphere sequence is a commutative monoid. Now symmetric spectra are modules over the sphere sequence, i.e. a sequence of spaces 
together with an action of the n-th symmetric group
on
and maps 
satisfying suitable equivariance conditions. The category of symmetric spectra has a monoidal product denoted by 
. A highly structured (commutative) ring spectrum is now defined to be a (commutative) monoid in symmetric spectra, called a (commutative) symmetric ring spectrum. This boils down to giving maps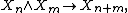
which satisfy suitable equivariance, unitality and associativity (and commutativity) conditions (see Schwede 2007).
There are several model structures on symmetric spectra, which have as homotopy the stable homotopy category. Also here it is true that the category of modules over an
-operad and the category of monoids
are Quillen equivalent
and likewise the category of modules over an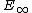
-operad and the category of commutative monoids.
A variant of symmetric spectra are orthogonal spectra, where one substitutes the symmetric group by the orthogonal group (see Mandell et al, 2001). They have the advantage that the naively defined homotopy groups coincide with those in the stable homotopy category, which is not the case for symmetric spectra. On the other hand, symmetric spectra have the advantage that they can also be defined for simplicial sets
. Symmetric and orthogonal spectra are arguably the simplest ways to construct a sensible symmetric monoidal category of spectra.
). One can also define infinity-versions of (commutative) monoids and then define
-ring spectra as monoids in spectra and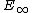 
-ring spectra as commutative monoids in spectra. This is worked out in Lurie's book Higher Algebra.
-ring spectra in symmetric/orthogonal spectra. The most fundamental example is the sphere spectrum with the (canonical) multiplication map 
. It is also not hard to write down multiplication maps for Eilenberg-MacLane spectra
(representing ordinary cohomology
) and certain Thom spectra (representing bordism theories). Topological (real or complex) K-theory is also an example, but harder to obtain: in symmetric spectra one uses a C*-algebra interpretation of K-theory, in the operad approach one uses a machine of multiplicative infinite loop space theory.
A more recent approach for finding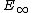
-refinements of mutliplicative cohomology theories is Goerss-Hopkins obstruction theory. It succeeded in finding 
-ring structures on Lubin-Tate spectra and on elliptic spectra
. By a similar (but older) method, it could also be shown that Morava K-theory
and also other variants of Brown-Peterson cohomology possess an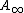
-ring structure (see e.g. Baker and Jeanneret, 2002). Recently, Basterra and Mandell have shown that Brown–Peterson cohomology has even an 
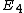-ring structure, where an 
-structure is defined by replacing the operad of infinite-dimensional cubes in infinite-dimensional space by 4-dimensional cubes in 4-dimensional space in the definition of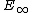 
-ring spectra. It can be shown that if Brown–Peterson cohomology
has an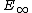
structure, it is not compatible with the usual map 
from complex cobordism (see Johnson, Noel 2010).
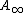-ring is an object in homotopy theory encoding a refinement of a multiplicative structure on a cohomology theory. A commutative version of an -ring is called an -ring. While originally motivated by questions of geometric topologyGeometric topology
In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.- Topics :...
and bundle theory, they are today most often used in stable homotopy theory
Stable homotopy theory
In mathematics, stable homotopy theory is that part of homotopy theory concerned with all structure and phenomena that remain after sufficiently many applications of the suspension functor...
.
Background
Highly structured ring spectra have better formal properties than multiplicative cohomology theories - a point utilized, for example, in the construction of topological modular formsTopological modular forms
In mathematics, the spectrum of topological modular forms describes a generalized cohomology theory whose coefficient ring is related to the graded ring of holomorphic modular forms with integral cusp expansions...
, and which has allowed also new constructions of more classical objects such as Morava K-theory
Morava K-theory
In stable homotopy theory, a branch of mathematics, Morava K-theory is one of a collection of cohomology theories introduced in algebraic topology by Jack Morava in unpublished preprints in the early 1970s...
. Beside their formal properties,
-structures are also important in calculations, since they allow for operations in the underlying cohomology theory, analogous to (and generalizing) the well-known Steenrod operationsSteenrod algebra
In algebraic topology, a Steenrod algebra was defined by to be the algebra of stable cohomology operations for mod p cohomology.For a given prime number p, the Steenrod algebra Ap is the graded Hopf algebra over the field Fp of order p, consisting of all stable cohomology operations for mod p...
in ordinary cohomology. As not every cohomology theory allows such operations, not every multiplicative structure may be refined to an
-structure and even in cases where this is possible, it may be a formidable task to prove that.The rough idea of highly structured ring spectra is the following: If multiplication in a cohomology theory (analogous to the multiplication in singular cohomology, inducing the cup product
Cup product
In mathematics, specifically in algebraic topology, the cup product is a method of adjoining two cocycles of degree p and q to form a composite cocycle of degree p + q. This defines an associative graded commutative product operation in cohomology, turning the cohomology of a space X into a...
) fulfills associativity (and commutativity) only up to homotopy, this is too lax for many constructions (e.g. for limits and colimits in the sense of category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
). On the other hand, requiring strict associativity (or commutativity) in a naive way is too restrictive for many of the wanted examples. A basic idea is that the relations need only hold up to homotopy, but these homotopies should fulfill again some homotopy relations, whose homotopies again fulfill some further homotopy conditions; and so on. The classical approach organizes this structure via operads, while the recent approach of Jacob Lurie
Jacob Lurie
Jacob Alexander Lurie is an American mathematician, who is currently a professor at Harvard University.-Life:While in school, Lurie took part in the International Mathematical Olympiad, where he won a gold medal with a perfect score in 1994...
deals with it in the language of
-categories. The most widely used approaches today employ the language of model categoriesModel category
In mathematics, particularly in homotopy theory, a model category is a category with distinguished classes of morphisms called 'weak equivalences', 'fibrations' and 'cofibrations'. These abstract from a conventional homotopy category, of topological spaces or of chain complexes...
.
All these approaches depend on building carefully an underlying category of Spectra
Spectrum (homotopy theory)
In algebraic topology, a branch of mathematics, a spectrum is an object representing a generalized cohomology theory. There are several different constructions of categories of spectra, any of which gives a context for the same stable homotopy theory....
.
Operads
The theory of operads is motivated by the study of loop spaces. A loop space ΩX has a multiplication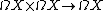by composition of loops. Here the two loops are sped up by a factor of 2 and the first takes the interval [0,1/2] and the second [1/2,1]. This product is not associative since the scalings are not compatible, but it is associative up to homotopy and the homotopies are coherent up to higher homotopies and so on. This situation can be made precise by saying that ΩX is an algebra over the little interval operad. This is an example of an
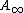-operad, i.e. an operad of topological spaces which is homotopy equivalent to the associative operad. An 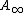-ring spectrum can now be imagined as an algebra over an -operad in a suitable category of spectra and suitable compatibility conditions (see May, 1977).For the definition of
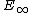-ring spectra essentially the same approach works, where one replaces the 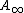-operad by an 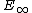-operad, i.e. an operad of contractible topological spaces. An example of such an operad can be again motivated by the study of loop spaces. The product of the double loop space is already commutative up to homotopy, but this homotopy fulfills no higher conditions. To get full coherence of higher homotopies one has to pass to the infinite loop space 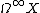. This leads to the in -cube operad of infinite-dimensional cubes in infinite-dimensional space, which is an example of an 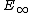-operad.The above approach was pioneered by J. Peter May
J. Peter May
Jon Peter May is an American mathematician, working in the fields of algebraic topology, category theory, homotopy theory, and the foundational aspects of spectra. He is known, in particular, for inventing the term operads and the May spectral sequence.He received a B.A. from Swarthmore College in...
. Together with Elmendorf, Kriz and Mandell he developed in the 90s a variant of his older definition of spectra, so called S-modules (see Elmendorf et al, 2007). S-modules possess a model structure, whose homotopy category is the stable homotopy category. In S-modules the category of modules over an
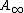-operad and the category of monoidsMonoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
are Quillen equivalent
Quillen adjunction
In homotopy theory, a branch of mathematics, a Quillen adjunction between two closed model categories C and D is a special kind of adjunction between categories that induces an adjunction between the homotopy categories Ho and Ho via the total derived functor construction...
and likewise the category of modules over an
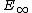-operad and the category of commutative monoids. Therefore is it possible to define 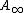-ring spectra and -ring spectra as (commutative) monoids in the category of S-modules, so called (commutative) S-algebras. Since (commutative) monoids are easier to deal with than algebras over complicated operads, this new approach is for many purposes more convenient. It should, however, be noted that the actual construction of the category of S-modules is technically quite complicated.Diagram spectra
Another approach to the goal of seeing highly structured ring spectra as monoids in a suitable category of spectra are categories of diagram spectra. Probably the most famous one of these is the category of symmetric spectra, pioneered by Jeff Smith. Its basic idea is the following:In the most naive sense, a spectrum is a sequence of (pointed) spaces
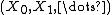together with maps 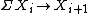, where ΣX denotes the suspension. Another viewpoint is the following: one considers the category of sequences of spaces together with the monoidalMonoidal category
In mathematics, a monoidal category is a category C equipped with a bifunctorwhich is associative, up to a natural isomorphism, and an object I which is both a left and right identity for ⊗, again up to a natural isomorphism...
structure given by a smash product
Smash product
In mathematics, the smash product of two pointed spaces X and Y is the quotient of the product space X × Y under the identifications ∼ for all x ∈ X and y ∈ Y. The smash product is usually denoted X ∧ Y...
. Then the sphere sequence
has the structure of a monoid and spectra are just modules over this monoid. If this monoid was commutative, then a monoidal structure on the category of modules over it would arise (as in algebraAlgebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
the modules over a commutative ring have a tensor product). But the monoid structure of the sphere sequence is not commutative due to different orderings of the coordinates.
The idea is now that one can build the coordinate changes into the definition of a sequence: a symmetric sequence is a sequence of spaces
together with an action of the n-th symmetric groupSymmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
on
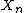. If one equips this with a suitable monoidal product, one gets that the sphere sequence is a commutative monoid. Now symmetric spectra are modules over the sphere sequence, i.e. a sequence of spaces together with an action of the n-th symmetric groupSymmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
on
and maps satisfying suitable equivariance conditions. The category of symmetric spectra has a monoidal product denoted by . A highly structured (commutative) ring spectrum is now defined to be a (commutative) monoid in symmetric spectra, called a (commutative) symmetric ring spectrum. This boils down to giving maps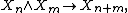which satisfy suitable equivariance, unitality and associativity (and commutativity) conditions (see Schwede 2007).
There are several model structures on symmetric spectra, which have as homotopy the stable homotopy category. Also here it is true that the category of modules over an
-operad and the category of monoidsMonoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
are Quillen equivalent
Quillen adjunction
In homotopy theory, a branch of mathematics, a Quillen adjunction between two closed model categories C and D is a special kind of adjunction between categories that induces an adjunction between the homotopy categories Ho and Ho via the total derived functor construction...
and likewise the category of modules over an
-operad and the category of commutative monoids.A variant of symmetric spectra are orthogonal spectra, where one substitutes the symmetric group by the orthogonal group (see Mandell et al, 2001). They have the advantage that the naively defined homotopy groups coincide with those in the stable homotopy category, which is not the case for symmetric spectra. On the other hand, symmetric spectra have the advantage that they can also be defined for simplicial sets
Simplicial set
In mathematics, a simplicial set is a construction in categorical homotopy theory which is a purely algebraic model of the notion of a "well-behaved" topological space...
. Symmetric and orthogonal spectra are arguably the simplest ways to construct a sensible symmetric monoidal category of spectra.
Infinity-categories
Infinity-categories are a variant of classical categories where composition of morphisms is not uniquely defined, but only up to contractible choice. In general, it does not make sense to say that a diagram commutes strictly in an infinity-category, but only that it commutes up to coherent homotopy. One can define an infinity-category of spectra (as done by LurieJacob Lurie
Jacob Alexander Lurie is an American mathematician, who is currently a professor at Harvard University.-Life:While in school, Lurie took part in the International Mathematical Olympiad, where he won a gold medal with a perfect score in 1994...
). One can also define infinity-versions of (commutative) monoids and then define
-ring spectra as monoids in spectra and 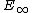-ring spectra as commutative monoids in spectra. This is worked out in Lurie's book Higher Algebra.Comparison
The categories of S-modules, symmetric and orthogonal spectra and their categories of (commutative) monoids admit comparisons via Quillen equivalences due to work of several mathematicians (including Schwede). In spite of this the model category of S-modules and the model category of symmetric spectra have quite different behaviour: in S-modules every object is fibrant (which is not true in symmetric spectra), while in symmetric spectra the sphere spectrum is cofibrant (which is not true in S-modules). By a theorem of Lewis, it is not possible to construct one category of spectra, which has all desired properties. A comparison of the infinity category approach to spectra with the more classical model category approach of symmetric spectra can be found in Lurie's Higher Algebra 4.4.4.9.Examples
It is easiest to write down concrete examples of-ring spectra in symmetric/orthogonal spectra. The most fundamental example is the sphere spectrum with the (canonical) multiplication map . It is also not hard to write down multiplication maps for Eilenberg-MacLane spectraSpectrum (homotopy theory)
In algebraic topology, a branch of mathematics, a spectrum is an object representing a generalized cohomology theory. There are several different constructions of categories of spectra, any of which gives a context for the same stable homotopy theory....
(representing ordinary cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
) and certain Thom spectra (representing bordism theories). Topological (real or complex) K-theory is also an example, but harder to obtain: in symmetric spectra one uses a C*-algebra interpretation of K-theory, in the operad approach one uses a machine of multiplicative infinite loop space theory.
A more recent approach for finding
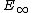-refinements of mutliplicative cohomology theories is Goerss-Hopkins obstruction theory. It succeeded in finding -ring structures on Lubin-Tate spectra and on elliptic spectraElliptic cohomology
In mathematics, elliptic cohomology is a cohomology theory in the sense of algebraic topology. It is related to elliptic curves and modular forms.-History and motivation:Historically, elliptic cohomology arose from the study of elliptic genera...
. By a similar (but older) method, it could also be shown that Morava K-theory
Morava K-theory
In stable homotopy theory, a branch of mathematics, Morava K-theory is one of a collection of cohomology theories introduced in algebraic topology by Jack Morava in unpublished preprints in the early 1970s...
and also other variants of Brown-Peterson cohomology possess an
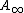-ring structure (see e.g. Baker and Jeanneret, 2002). Recently, Basterra and Mandell have shown that Brown–Peterson cohomology has even an 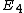-ring structure, where an -structure is defined by replacing the operad of infinite-dimensional cubes in infinite-dimensional space by 4-dimensional cubes in 4-dimensional space in the definition of 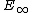-ring spectra. It can be shown that if Brown–Peterson cohomologyBrown–Peterson cohomology
In mathematics, Brown–Peterson cohomology is a generalized cohomology theory introduced by, depending on a choice of prime p. It is described in detail by .Its representing spectrum is denoted by BP.-Complex cobordism and Quillen's idempotent:...
has an
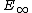structure, it is not compatible with the usual map from complex cobordism (see Johnson, Noel 2010).Constructions
One of the main advantage of highly structured ring spectra is that they allow many constructions.- They form a model category and therefore one can take (homotopy) limits and colimits.
- Modules over a highly structured ring spectrum form a stable model category. In particular, their homotopy category is triangulated. If the ring spectrum has an
-structure, the category of modules has a monoidal (smash) product; if it is at least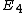 
, then it has a symmetric monoidal (smash) product. - One can form group ring spectra.
- One can define the algebraic K-theoryAlgebraic K-theoryIn mathematics, algebraic K-theory is an important part of homological algebra concerned with defining and applying a sequenceof functors from rings to abelian groups, for all integers n....
/topological Hochschild homologyHochschild homologyIn mathematics, Hochschild homology is a homology theory for associative algebras over rings. There is also a theory for Hochschild homology of certain functors...
/... of a highly structured ring spectrum - One can define the space of units, which is crucial for certain questions of orientability (of bundles).