Herbrand–Ribet theorem
Encyclopedia
In mathematics
, the Herbrand–Ribet theorem is a result on the class number
of certain number fields. It is a strengthening of Ernst Kummer
's theorem to the effect that the prime p divides the class number
of the cyclotomic field
of p-th roots of unity if and only if
p divides the numerator of the n-th Bernoulli number
Bn
for some n, 0 < n < p − 1. The Herbrand–Ribet theorem specifies what, in particular, it means when p divides such an Bn.
The Galois group
Δ of the cyclotomic field
of pth roots of unity for an odd prime p, Q(ζ) with ζp = 1, consists of the p − 1 group elements σa, where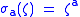
. As a consequence of the Fermat's little theorem
, in the ring of p-adic integers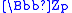
we have p − 1 roots of unity, each of which is congruent mod p to some number in the range 1 to p − 1; we can therefore define a Dirichlet character
ω (the Teichmüller character) with values in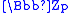
by requiring that for n relatively prime to p, ω(n) be congruent to n modulo p. The p part of the class group is a 
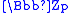-module (since it is p-primary), hence a module over the group ring
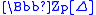. We now define idempotent elements of the group ring for each n from 1 to p − 1, as
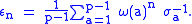
It is easy to see that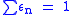
and 
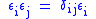where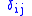 
is the Kronecker delta. This allows us to break up the p part of the ideal class group G of Q(ζ) by means of the idempotents; if G is the ideal class group, then, letting Gn = εn(G), we have 
.
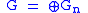The Herbrand–Ribet theorem states that Gn is nontrivial if and only if p divides the Bernoulli number Bp−n. The part saying p divides Bp−n if Gn is not trivial is due to Jacques Herbrand
. The converse, that if p divides Bp−n then Gn is not trivial is due to Kenneth Ribet, and is considerably more difficult. By class field theory
, this can only be true if there is an unramified extension of the field of pth roots of unity by a cyclic extension of degree p which behaves in the specified way under the action of Σ; Ribet proves this by actually constructing such an extension using methods in the theory of modular forms. A more elementary proof of Ribet's converse to Herbrand's theorem, a consequence of the theory of Euler systems, can be found in Washington's book.
Ribet's methods were pushed further by Barry Mazur
and Andrew Wiles
in order to prove the Main Conjecture of Iwasawa theory, a corollary of which is a strengthening of the Herbrand-Ribet theorem: the power of p dividing Bp−n is exactly the power of p dividing the order of Gn.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Herbrand–Ribet theorem is a result on the class number
Class number
In mathematics, class number may refer to* Class number , the number of conjugacy classes of a group*The size of the ideal class group of a number ring*The number of equivalence classes of binary quadratic forms of a given discriminant...
of certain number fields. It is a strengthening of Ernst Kummer
Ernst Kummer
Ernst Eduard Kummer was a German mathematician. Skilled in applied mathematics, Kummer trained German army officers in ballistics; afterwards, he taught for 10 years in a gymnasium, the German equivalent of high school, where he inspired the mathematical career of Leopold Kronecker.-Life:Kummer...
's theorem to the effect that the prime p divides the class number
Ideal class group
In mathematics, the extent to which unique factorization fails in the ring of integers of an algebraic number field can be described by a certain group known as an ideal class group...
of the cyclotomic field
Cyclotomic field
In number theory, a cyclotomic field is a number field obtained by adjoining a complex primitive root of unity to Q, the field of rational numbers...
of p-th roots of unity if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
p divides the numerator of the n-th Bernoulli number
Bernoulli number
In mathematics, the Bernoulli numbers Bn are a sequence of rational numbers with deep connections to number theory. They are closely related to the values of the Riemann zeta function at negative integers....
Bn
for some n, 0 < n < p − 1. The Herbrand–Ribet theorem specifies what, in particular, it means when p divides such an Bn.
The Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
Δ of the cyclotomic field
Cyclotomic field
In number theory, a cyclotomic field is a number field obtained by adjoining a complex primitive root of unity to Q, the field of rational numbers...
of pth roots of unity for an odd prime p, Q(ζ) with ζp = 1, consists of the p − 1 group elements σa, where
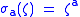. As a consequence of the Fermat's little theoremFermat's little theorem
Fermat's little theorem states that if p is a prime number, then for any integer a, a p − a will be evenly divisible by p...
, in the ring of p-adic integers
we have p − 1 roots of unity, each of which is congruent mod p to some number in the range 1 to p − 1; we can therefore define a Dirichlet characterDirichlet character
In number theory, Dirichlet characters are certain arithmetic functions which arise from completely multiplicative characters on the units of \mathbb Z / k \mathbb Z...
ω (the Teichmüller character) with values in
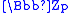by requiring that for n relatively prime to p, ω(n) be congruent to n modulo p. The p part of the class group is a 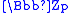-module (since it is p-primary), hence a module over the group ringGroup ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
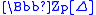. We now define idempotent elements of the group ring for each n from 1 to p − 1, as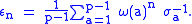It is easy to see that
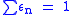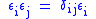and where 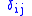is the Kronecker delta. This allows us to break up the p part of the ideal class group G of Q(ζ) by means of the idempotents; if G is the ideal class group, then, letting Gn = εn(G), we have 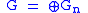.The Herbrand–Ribet theorem states that Gn is nontrivial if and only if p divides the Bernoulli number Bp−n. The part saying p divides Bp−n if Gn is not trivial is due to Jacques Herbrand
Jacques Herbrand
Jacques Herbrand was a French mathematician who was born in Paris, France and died in La Bérarde, Isère, France. Although he died at only 23 years of age, he was already considered one of "the greatest mathematicians of the younger generation" by his professors Helmut Hasse, and Richard Courant.He...
. The converse, that if p divides Bp−n then Gn is not trivial is due to Kenneth Ribet, and is considerably more difficult. By class field theory
Class field theory
In mathematics, class field theory is a major branch of algebraic number theory that studies abelian extensions of number fields.Most of the central results in this area were proved in the period between 1900 and 1950...
, this can only be true if there is an unramified extension of the field of pth roots of unity by a cyclic extension of degree p which behaves in the specified way under the action of Σ; Ribet proves this by actually constructing such an extension using methods in the theory of modular forms. A more elementary proof of Ribet's converse to Herbrand's theorem, a consequence of the theory of Euler systems, can be found in Washington's book.
Ribet's methods were pushed further by Barry Mazur
Barry Mazur
-Life:Born in New York City, Mazur attended the Bronx High School of Science and MIT, although he did not graduate from the latter on account of failing a then-present ROTC requirement. Regardless, he was accepted for graduate school and received his Ph.D. from Princeton University in 1959,...
and Andrew Wiles
Andrew Wiles
Sir Andrew John Wiles KBE FRS is a British mathematician and a Royal Society Research Professor at Oxford University, specializing in number theory...
in order to prove the Main Conjecture of Iwasawa theory, a corollary of which is a strengthening of the Herbrand-Ribet theorem: the power of p dividing Bp−n is exactly the power of p dividing the order of Gn.