Henagon
Encyclopedia
In geometry
a henagon (or monogon) is a polygon
with one edge
and one vertex
. It has Schläfli symbol {1}. Since a henagon has only one side and only one interior angle, every henagon is regular
by definition.
a henagon is usually considered to be an impossible object, because its endpoints must coincide, unlike any Euclidean line segment. For this reason, most authorities do not consider the henagon as a proper polygon in Euclidean geometry.
, on the other hand, a finite henagon can be drawn by placing a single vertex anywhere on a great circle
. Two henagons can be used to construct a dihedron
on a sphere, with Schläfli symbol, {1,2}.
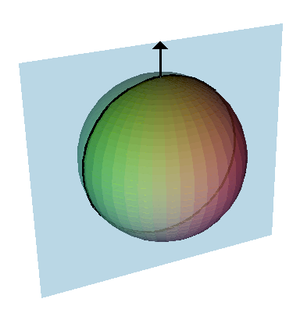The henagon can be used in spherical polyhedra
, for example the henagonal dihedron
{1, 2}, the digonal hosohedron {2, 1} and the henagonal henahedron {1, 1}. The henagonal henahedron consists of a single vertex, no edges and a single face (the whole sphere minus the vertex.)
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
a henagon (or monogon) is a polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
with one edge
Edge (geometry)
In geometry, an edge is a one-dimensional line segment joining two adjacent zero-dimensional vertices in a polygon. Thus applied, an edge is a connector for a one-dimensional line segment and two zero-dimensional objects....
and one vertex
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
. It has Schläfli symbol {1}. Since a henagon has only one side and only one interior angle, every henagon is regular
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
by definition.
In Euclidean geometry
In Euclidean geometryEuclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
a henagon is usually considered to be an impossible object, because its endpoints must coincide, unlike any Euclidean line segment. For this reason, most authorities do not consider the henagon as a proper polygon in Euclidean geometry.
In spherical geometry
In spherical geometrySpherical geometry
Spherical geometry is the geometry of the two-dimensional surface of a sphere. It is an example of a geometry which is not Euclidean. Two practical applications of the principles of spherical geometry are to navigation and astronomy....
, on the other hand, a finite henagon can be drawn by placing a single vertex anywhere on a great circle
Great circle
A great circle, also known as a Riemannian circle, of a sphere is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center...
. Two henagons can be used to construct a dihedron
Dihedron
A dihedron is a type of polyhedron, made of two polygon faces which share the same set of edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is...
on a sphere, with Schläfli symbol, {1,2}.
Spherical polyhedron
In mathematics, a spherical polyhedron is a tiling of the sphere in which the surface is divided or partitioned by great arcs into bounded regions called spherical polygons...
, for example the henagonal dihedron
Dihedron
A dihedron is a type of polyhedron, made of two polygon faces which share the same set of edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is...
{1, 2}, the digonal hosohedron {2, 1} and the henagonal henahedron {1, 1}. The henagonal henahedron consists of a single vertex, no edges and a single face (the whole sphere minus the vertex.)