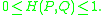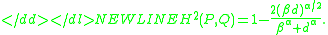Hellinger distance
Encyclopedia
In probability
and statistics
, the Hellinger distance is used to quantify the similarity between two probability distributions. It is a type of f-divergence
. The Hellinger distance is defined in terms of the Hellinger integral
, which was introduced by Ernst Hellinger
.
To define the Hellinger distance in terms of measure theory, let P and Q denote two probability measure
s that are absolutely continuous
with respect to a third probability measure λ. The square of the Hellinger distance between P and Q is defined as the quantity
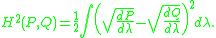
Here, dP / dλ and dQ / dλ are the Radon–Nikodym derivatives of P and Q respectively. This definition does not depend on λ, so the Hellinger distance between P and Q does not change if λ is replaced with a different probability measure with respect to which both P and Q are absolutely continuous. For compactness, the above formula is often written as
To define the Hellinger distance in terms of elementary probability theory, we take λ to be Lebesgue measure
, so that dP / dλ and dQ / dλ are simply probability density function
s. If we denote the densities as f and g, respectively, the squared Hellinger distance can be expressed as a standard calculus integral
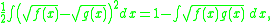
where the second form can be obtained by expanding the square and using the fact that the integral of a probability density over its domain must be one.
The Hellinger distance H(P, Q) satisfies the property (derivable from the Cauchy-Schwarz inequality)
The maximum distance 1 is achieved when P assigns probability zero to every set to which Q assigns a positive probability, and vice versa.
Sometimes the factor 1/2 in front of the integral is omitted, in which case the Hellinger distance ranges from zero to the square root of two.
The Hellinger distance is related to the Bhattacharyya coefficient
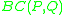as it can be defined as
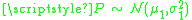and 
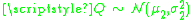is:
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Mathematical statistics
Mathematical statistics is the study of statistics from a mathematical standpoint, using probability theory as well as other branches of mathematics such as linear algebra and analysis...
, the Hellinger distance is used to quantify the similarity between two probability distributions. It is a type of f-divergence
F-divergence
In probability theory, an ƒ-divergence is a function Df that measures the difference between two probability distributions P and Q...
. The Hellinger distance is defined in terms of the Hellinger integral
Hellinger integral
In mathematics, the Hellinger integral is an integral introduced by that is a special case of the Kolmogorov integral. It is used to define the Hellinger distance in probability theory.-References:...
, which was introduced by Ernst Hellinger
Ernst Hellinger
Ernst David Hellinger was a German mathematician.-Early years:Ernst Hellinger was born on September 30, 1883 in Striegau, Silesia, Germany to Emil and Julie Hellinger. He grew up in Breslau, attended school and graduated from the Gymnasium there in 1902...
.
To define the Hellinger distance in terms of measure theory, let P and Q denote two probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
s that are absolutely continuous
Absolute continuity
In mathematics, the relationship between the two central operations of calculus, differentiation and integration, stated by fundamental theorem of calculus in the framework of Riemann integration, is generalized in several directions, using Lebesgue integration and absolute continuity...
with respect to a third probability measure λ. The square of the Hellinger distance between P and Q is defined as the quantity
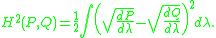
Here, dP / dλ and dQ / dλ are the Radon–Nikodym derivatives of P and Q respectively. This definition does not depend on λ, so the Hellinger distance between P and Q does not change if λ is replaced with a different probability measure with respect to which both P and Q are absolutely continuous. For compactness, the above formula is often written as
To define the Hellinger distance in terms of elementary probability theory, we take λ to be Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
, so that dP / dλ and dQ / dλ are simply probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
s. If we denote the densities as f and g, respectively, the squared Hellinger distance can be expressed as a standard calculus integral
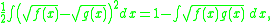
where the second form can be obtained by expanding the square and using the fact that the integral of a probability density over its domain must be one.
The Hellinger distance H(P, Q) satisfies the property (derivable from the Cauchy-Schwarz inequality)
The maximum distance 1 is achieved when P assigns probability zero to every set to which Q assigns a positive probability, and vice versa.
Sometimes the factor 1/2 in front of the integral is omitted, in which case the Hellinger distance ranges from zero to the square root of two.
The Hellinger distance is related to the Bhattacharyya coefficient
Bhattacharyya distance
In statistics, the Bhattacharyya distance measures the similarity of two discrete or continuous probability distributions. It is closely related to the Bhattacharyya coefficient which is a measure of the amount of overlap between two statistical samples or populations. Both measures are named after A...
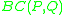as it can be defined as
Examples
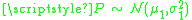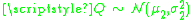The squared Hellinger distance between two normal distributions and is:
-
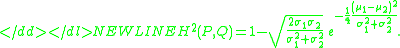
The squared Hellinger distance between two exponential distributionExponential distributionIn probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
s
and 
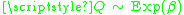is:
-
The squared Hellinger distance between two Weibull distributions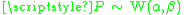
and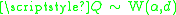 
(where 
is a common shape parameter and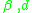 
are the scale parameters respectively):
-
-
