Heawood number
Encyclopedia
In mathematics
, the Heawood number of a surface
is a certain upper bound
for the maximal number of colors needed to color any graph
embedded
in the surface.
In 1890 Heawood proved for all surfaces except the sphere
that no more than
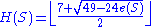
colors are needed to color any graph embedded in a surface of Euler characteristic
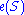 . The case of the sphere is the four-color conjecture which was settled by Kenneth Appel
. The case of the sphere is the four-color conjecture which was settled by Kenneth Appel
and Wolfgang Haken
in 1976. The number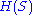 became known as Heawood number in 1976.
became known as Heawood number in 1976.
Franklin proved that the chromatic number of a graph embedded in the Klein bottle
can be as large as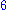 , but never exceeds
, but never exceeds 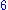 . Later it was proved in the works of Gerhard Ringel
. Later it was proved in the works of Gerhard Ringel
and J. W. T. Youngs that the complete graph
of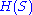 vertices can be embedded in the surface
vertices can be embedded in the surface 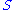 unless
unless  is the Klein bottle
is the Klein bottle
. This established that Heawood's bound could not be improved.
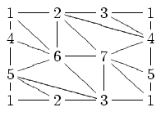
For example, the complete graph on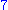 vertices can be embedded in the torus
vertices can be embedded in the torus
as follows:

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Heawood number of a surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
is a certain upper bound
Upper bound
In mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...
for the maximal number of colors needed to color any graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
embedded
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
in the surface.
In 1890 Heawood proved for all surfaces except the sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
that no more than
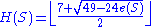
colors are needed to color any graph embedded in a surface of Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
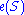 . The case of the sphere is the four-color conjecture which was settled by Kenneth Appel
. The case of the sphere is the four-color conjecture which was settled by Kenneth AppelKenneth Appel
Kenneth Ira Appel is a mathematician who in 1976, with colleague Wolfgang Haken at the University of Illinois at Urbana-Champaign, solved one of the most famous problems in mathematics, the four-color theorem...
and Wolfgang Haken
Wolfgang Haken
Wolfgang Haken is a mathematician who specializes in topology, in particular 3-manifolds.In 1976 together with colleague Kenneth Appel at the University of Illinois at Urbana-Champaign, Haken solved one of the most famous problems in mathematics, the four-color theorem...
in 1976. The number
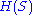 became known as Heawood number in 1976.
became known as Heawood number in 1976.Franklin proved that the chromatic number of a graph embedded in the Klein bottle
Klein bottle
In mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...
can be as large as
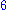 , but never exceeds
, but never exceeds 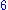 . Later it was proved in the works of Gerhard Ringel
. Later it was proved in the works of Gerhard RingelGerhard Ringel
Gerhard Ringel was a German mathematician who earned his Ph.D. from the University of Bonn in 1951...
and J. W. T. Youngs that the complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
of
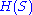 vertices can be embedded in the surface
vertices can be embedded in the surface 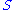 unless
unless  is the Klein bottle
is the Klein bottleKlein bottle
In mathematics, the Klein bottle is a non-orientable surface, informally, a surface in which notions of left and right cannot be consistently defined. Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a...
. This established that Heawood's bound could not be improved.
For example, the complete graph on
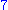 vertices can be embedded in the torus
vertices can be embedded in the torusTorus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
as follows:


