
Harish-Chandra's Schwartz space
Encyclopedia
In mathematical abstract harmonic analysis
, Harish-Chandra's Schwartz space is a space of functions on a semisimple Lie group whose derivatives are rapidly decreasing, studied by . It is an analogue of the Schwartz space on a real vector space
, and is used to define the space of tempered distribution
s on a semisimple Lie group.
and his σ function. The σ function is defined by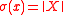
for x=k exp X with k in K and X in p for a Cartan decomposition
G = K exp p of the Lie group G, where ||X|| is a K-invariant Euclidean norm on p, usually chosen to be the Killing form
. .
The Schwartz space on G consists roughly of the functions all of whose derivatives are rapidly decreasing compared to Ξ. More precisely, if G is connected then the Schwartz space consists of all smooth functions f on G such that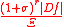
is bounded, where D is a product of left-invariant and right-invariant differential operators on G .
Harmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
, Harish-Chandra's Schwartz space is a space of functions on a semisimple Lie group whose derivatives are rapidly decreasing, studied by . It is an analogue of the Schwartz space on a real vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
, and is used to define the space of tempered distribution
Tempered distribution
*Distribution *Tempered representation...
s on a semisimple Lie group.
Definition
The definition of the Schwartz space uses Harish-Chandra's Ξ functionHarish-Chandra's Ξ function
In mathematical harmonic analysis, Harish-Chandra's Ξ function is a special spherical function on a semisimple Lie group, studied by .Harish-Chandra used it to define Harish-Chandra's Schwartz space....
and his σ function. The σ function is defined by
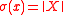
for x=k exp X with k in K and X in p for a Cartan decomposition
Cartan decomposition
The Cartan decomposition is a decomposition of a semisimple Lie group or Lie algebra, which plays an important role in their structure theory and representation theory. It generalizes the polar decomposition of matrices.- Cartan involutions on Lie algebras :...
G = K exp p of the Lie group G, where ||X|| is a K-invariant Euclidean norm on p, usually chosen to be the Killing form
Killing form
In mathematics, the Killing form, named after Wilhelm Killing, is a symmetric bilinear form that plays a basic role in the theories of Lie groups and Lie algebras...
. .
The Schwartz space on G consists roughly of the functions all of whose derivatives are rapidly decreasing compared to Ξ. More precisely, if G is connected then the Schwartz space consists of all smooth functions f on G such that
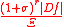
is bounded, where D is a product of left-invariant and right-invariant differential operators on G .

