
Hard hexagon model
Encyclopedia
In statistical mechanics
, the hard hexagon model is a 2-dimensional lattice model
of a gas, where particles are allowed to be on the vertices of a triangular lattice
but no two particles may be adjacent.
The model was solved by , who found that it was related to the Rogers-Ramanujan identities
.
is
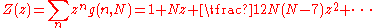
where g(n, N) is the number of ways of placing n particles on distinct lattice sites such that no 2 are adjacent. The variable z is called the activity and larger values correspond roughly to denser configurations. The function κ is defined by
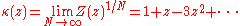
so that log(κ) is the free energy per unit site. Solving the hard hexagon model means (roughly) finding an exact expression for κ as a function of z.
The mean density ρ is given for small z by
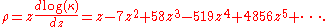
The vertices of the lattice fall into 3 classes numbered 1, 2, and 3, given by the 3 different ways to fill space with hard hexagons. There are 3 local densities ρ1, ρ2, ρ3, corresponding to the 3 classes of sites. When the activity is large the system approximates one of these 3 packings, so the local densities differ, but when the activity is below a critical point the three local densities are the same. The critical point separating the low-activity homogeneous phase from the high-activity ordered phase is zc = (11 + 53/2)/2 = 11.0917.... Above the critical point the local densities differ and in the phase where most hexagons are on sites of type 1 can be expanded as
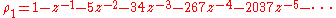

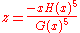
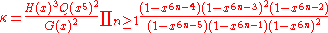
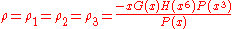
where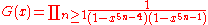
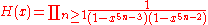
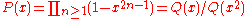
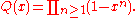
For large z > zc the solution (in the phase where most occupied sites have type 1) is given by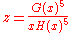
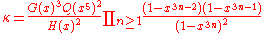
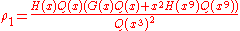
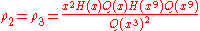
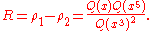
The functions G and H turn up in the Rogers-Ramanujan identities
, and the function Q is more or less the Dedekind eta function
. If x = e2πiτ, then q−1/60G(x), x11/60H(x), x−1/24P(x), z, κ, ρ, ρ1, ρ2, and ρ3 are modular functions of τ, while x1/24Q(x) is a modular form of weight 1/2. Since any two modular functions are related by an algebraic relation, this implies that the functions κ, z, R, ρ are all algebraic functions of each other (of quite high degree) .
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, the hard hexagon model is a 2-dimensional lattice model
Lattice model (physics)
In physics, a lattice model is a physical model that is defined on a lattice, as opposed to the continuum of space or spacetime. Lattice models originally occurred in the context of condensed matter physics, where the atoms of a crystal automatically form a lattice. Currently, lattice models are...
of a gas, where particles are allowed to be on the vertices of a triangular lattice
Hexagonal lattice
The hexagonal lattice or equilateral triangular lattice is one of the five 2D lattice types.Three nearby points form an equilateral triangle. In images four orientations of such a triangle are by far the most common...
but no two particles may be adjacent.
The model was solved by , who found that it was related to the Rogers-Ramanujan identities
Rogers-Ramanujan identities
In mathematics, the Rogers–Ramanujan identities are two identities related to basic hypergeometric series, first discovered and proved by . They were subsequently rediscovered by Srinivasa Ramanujan some time before 1913. Ramanujan had no proof, but rediscovered Rogers's paper in 1917, and they...
.
The partition function of the hard hexagon model
For a triangular lattice with N sites, the partition functionPartition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
is
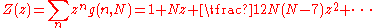
where g(n, N) is the number of ways of placing n particles on distinct lattice sites such that no 2 are adjacent. The variable z is called the activity and larger values correspond roughly to denser configurations. The function κ is defined by
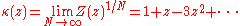
so that log(κ) is the free energy per unit site. Solving the hard hexagon model means (roughly) finding an exact expression for κ as a function of z.
The mean density ρ is given for small z by
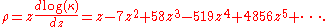
The vertices of the lattice fall into 3 classes numbered 1, 2, and 3, given by the 3 different ways to fill space with hard hexagons. There are 3 local densities ρ1, ρ2, ρ3, corresponding to the 3 classes of sites. When the activity is large the system approximates one of these 3 packings, so the local densities differ, but when the activity is below a critical point the three local densities are the same. The critical point separating the low-activity homogeneous phase from the high-activity ordered phase is zc = (11 + 53/2)/2 = 11.0917.... Above the critical point the local densities differ and in the phase where most hexagons are on sites of type 1 can be expanded as
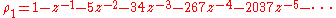

Solution
The solution is given for small values of z < zc by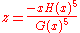
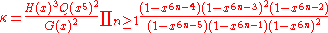
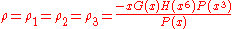
where
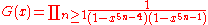
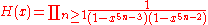
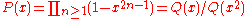
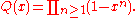
For large z > zc the solution (in the phase where most occupied sites have type 1) is given by
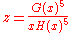
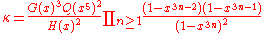
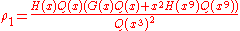
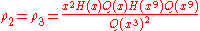
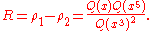
The functions G and H turn up in the Rogers-Ramanujan identities
Rogers-Ramanujan identities
In mathematics, the Rogers–Ramanujan identities are two identities related to basic hypergeometric series, first discovered and proved by . They were subsequently rediscovered by Srinivasa Ramanujan some time before 1913. Ramanujan had no proof, but rediscovered Rogers's paper in 1917, and they...
, and the function Q is more or less the Dedekind eta function
Dedekind eta function
The Dedekind eta function, named after Richard Dedekind, is a function defined on the upper half-plane of complex numbers, where the imaginary part is positive...
. If x = e2πiτ, then q−1/60G(x), x11/60H(x), x−1/24P(x), z, κ, ρ, ρ1, ρ2, and ρ3 are modular functions of τ, while x1/24Q(x) is a modular form of weight 1/2. Since any two modular functions are related by an algebraic relation, this implies that the functions κ, z, R, ρ are all algebraic functions of each other (of quite high degree) .

