Rogers-Ramanujan identities
Encyclopedia
In mathematics
, the Rogers–Ramanujan identities are two identities related to basic hypergeometric series
, first discovered and proved by . They were subsequently rediscovered (without a proof) by Srinivasa Ramanujan
some time before 1913. Ramanujan had no proof, but rediscovered Rogers's paper in 1917, and they then published a joint new proof . independently rediscovered and proved the identities.
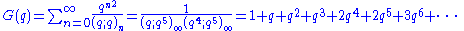
and
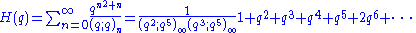 .
.
Here,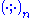 denotes the q-Pochhammer symbol.
denotes the q-Pochhammer symbol.
in statistical mechanics.
Ramanujan's continued fraction is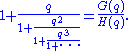
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Rogers–Ramanujan identities are two identities related to basic hypergeometric series
Basic hypergeometric series
In mathematics, Heine's basic hypergeometric series, or hypergeometric q-series, are q-analog generalizations of generalized hypergeometric series, and are in turn generalized by elliptic hypergeometric series....
, first discovered and proved by . They were subsequently rediscovered (without a proof) by Srinivasa Ramanujan
Srinivasa Ramanujan
Srīnivāsa Aiyangār Rāmānujan FRS, better known as Srinivasa Iyengar Ramanujan was a Indian mathematician and autodidact who, with almost no formal training in pure mathematics, made extraordinary contributions to mathematical analysis, number theory, infinite series and continued fractions...
some time before 1913. Ramanujan had no proof, but rediscovered Rogers's paper in 1917, and they then published a joint new proof . independently rediscovered and proved the identities.
Definition
The Rogers–Ramanujan identities are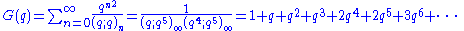
and
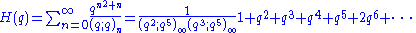 .
.Here,
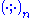 denotes the q-Pochhammer symbol.
denotes the q-Pochhammer symbol.Modular functions
If q = e2πiτ, then q−1/60G(q) and q11/60H(q) are modular functions of τ.Applications
The Rogers–Ramanujan identities appeared in Baxter's solution of the hard hexagon modelHard hexagon model
In statistical mechanics, the hard hexagon model is a 2-dimensional lattice model of a gas, where particles are allowed to be on the vertices of a triangular lattice but no two particles may be adjacent....
in statistical mechanics.
Ramanujan's continued fraction is