
Erdos–Szekeres theorem
Encyclopedia
In mathematics
, the Erdős–Szekeres theorem is a finitary result that makes precise one of the corollaries of Ramsey's theorem
. While Ramsey's theorem makes it easy to prove that every sequence of distinct real numbers contains either a monotonically increasing infinite subsequence
, or a monotonically decreasing infinite subsequence, the result proved by Paul Erdős
and George Szekeres
goes further. For given r, s they showed that any sequence of length at least (r − 1)(s − 1) + 1 contains either a monotonically increasing subsequence of length r, or a monotonically decreasing subsequence of length s. The proof appeared in the same 1935 paper that mentions the Happy Ending problem
.
An example of rs − r − s + 1 points without such a path, showing that this bound is tight, can be formed by applying a small rotation to an (r − 1) by (s − 1) grid.
credits this proof to the one-page paper of and calls it "the slickest and most systematic" of the proofs he surveys.
on chain decompositions in partial orders, or its simpler dual (Mirsky's theorem).
To prove the theorem, define a partial ordering on the members of the sequence, in which x is less than or equal to y in the partial order if x ≤ y as numbers and x is not later than y in the sequence. A chain in this partial order is a monotonically increasing subsequence, and an antichain
is a monotonically decreasing subsequence. By Mirsky's theorem, either there is a chain of length r, or the sequence can be partitioned into at most r − 1 antichains; but in that case the largest of the antichains must form a decreasing subsequence with length at least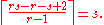
Alternatively, by Dilworth's theorem itself, either there is an antichain of length s, or the sequence can be partitioned into at most s − 1 chains, the longest of which must have length at least r.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Erdős–Szekeres theorem is a finitary result that makes precise one of the corollaries of Ramsey's theorem
Ramsey's theorem
In combinatorics, Ramsey's theorem states that in any colouring of the edges of a sufficiently large complete graph, one will find monochromatic complete subgraphs...
. While Ramsey's theorem makes it easy to prove that every sequence of distinct real numbers contains either a monotonically increasing infinite subsequence
Subsequence
In mathematics, a subsequence is a sequence that can be derived from another sequence by deleting some elements without changing the order of the remaining elements...
, or a monotonically decreasing infinite subsequence, the result proved by Paul Erdős
Paul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
and George Szekeres
George Szekeres
George Szekeres AM was a Hungarian-Australian mathematician.-Early years:Szekeres was born in Budapest, Hungary as Szekeres György and received his degree in chemistry at the Technical University of Budapest. He worked six years in Budapest as an analytical chemist. He married Esther Klein in 1936...
goes further. For given r, s they showed that any sequence of length at least (r − 1)(s − 1) + 1 contains either a monotonically increasing subsequence of length r, or a monotonically decreasing subsequence of length s. The proof appeared in the same 1935 paper that mentions the Happy Ending problem
Happy Ending problem
The Happy Ending problem is the following statement:This was one of the original results that led to the development of Ramsey theory....
.
Example
For r = 3 and s = 2, the formula tells us that any permutation of three numbers has an increasing subsequence of length three or a decreasing subsequence of length two. Among the six permutations of the numbers 1,2,3:- 1,2,3 has an increasing subsequence consisting of all three numbers
- 1,3,2 has a decreasing subsequence 3,2
- 2,1,3 has a decreasing subsequence 2,1
- 2,3,1 has two decreasing subsequences, 2,1 and 3,1
- 3,1,2 has two decreasing subsequences, 3,1 and 3,2
- 3,2,1 has three decreasing length-2 subsequences, 3,2, 3,1, and 2,1.
Geometric interpretation
One can interpret the positions of the numbers in a sequence as x-coordinates of points in the Euclidean plane, and the numbers themselves as y-coordinates; conversely, for any point set in the plane, the y-coordinates of the points, ordered by their x-coordinates, forms a sequence of numbers (unless two of the points have equal x-coordinates). With this translation between sequences and point sets, the Erdős–Szekeres theorem can be interpreted as stating that in any set of at least rs − r − s + 2 points we can find a polygonal path of either r − 1 positive-slope edges or s − 1 negative-slope edges. For instance, taking r = s = 5, any set of at least 17 points has a four-edge path in which all slopes have the same sign.An example of rs − r − s + 1 points without such a path, showing that this bound is tight, can be formed by applying a small rotation to an (r − 1) by (s − 1) grid.
Proofs
The Erdős–Szekeres theorem can be proved in several different ways; surveys six different proofs of the Erdős–Szekeres theorem, including the following two. Other proofs surveyed by Steele include the original proof by Erdős and Szekeres as well as those of , , and .Pigeonhole principle
Given a sequence of length (r − 1)(s − 1) + 1, label each number ni in the sequence with the pair (ai,bi), where ai is the length of the longest monotonically increasing subsequence ending with ni and bi is the length of the longest monotonically decreasing subsequence ending with ni. Each two numbers in the sequence are labeled with a different pair: if and then , and on the other hand if then . But there are only (r − 1)(s − 1) possible labels in which ai is at most r − 1 and bi is at most s − 1, so by the pigeonhole principle there must exist a value of i for which ai or bi is outside this range. If ai is out of range then ni is part of an increasing sequence of length at least r, and if bi is out of range then ni is part of a decreasing sequence of length at least s.credits this proof to the one-page paper of and calls it "the slickest and most systematic" of the proofs he surveys.
Dilworth's theorem
Another of the proofs uses Dilworth's theoremDilworth's theorem
In mathematics, in the areas of order theory and combinatorics, Dilworth's theorem characterizes the width of any finite partially ordered set in terms of a partition of the order into a minimum number of chains...
on chain decompositions in partial orders, or its simpler dual (Mirsky's theorem).
To prove the theorem, define a partial ordering on the members of the sequence, in which x is less than or equal to y in the partial order if x ≤ y as numbers and x is not later than y in the sequence. A chain in this partial order is a monotonically increasing subsequence, and an antichain
Antichain
In mathematics, in the area of order theory, an antichain is a subset of a partially ordered set such that any two elements in the subset are incomparable. Let S be a partially ordered set...
is a monotonically decreasing subsequence. By Mirsky's theorem, either there is a chain of length r, or the sequence can be partitioned into at most r − 1 antichains; but in that case the largest of the antichains must form a decreasing subsequence with length at least
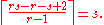
Alternatively, by Dilworth's theorem itself, either there is an antichain of length s, or the sequence can be partitioned into at most s − 1 chains, the longest of which must have length at least r.

