
Cyclic polytope
Encyclopedia
In mathematics, a cyclic polytope, denoted C(n,d), is a convex polytope
formed as a convex hull of n distinct points on a rational normal curve in Rd, where n is greater than d. These polytopes were studied by Constantin Carathéodory
, David Gale
, Theodore Motzkin
, Victor Klee
, and others. They play an important role in polyhedral combinatorics
: according to the Upper Bound Conjecture, proved by Peter McMullen and Richard Stanley
, the boundary Δ(n,d) of the cyclic polytope C(n,d) maximizes the number fi of i-dimensional faces among all simplicial spheres of dimension d − 1 with n vertices.
 is defined by
is defined by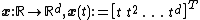 .
.
The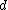 -dimensional cyclic polytope
-dimensional cyclic polytope
with vertices is the convex hull
vertices is the convex hull

of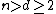 distinct points
distinct points 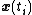 with
with 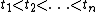 on the moment curve.
on the moment curve.
The combinatorial structure of this polytope is independent of the points chosen, and the resulting polytope has dimension d and n vertices. Its boundary is a (d − 1)-dimensional simplicial polytope
denoted Δ(n,d).
.
Let . Then, a
. Then, a  -subset
-subset 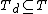 forms a facet of
forms a facet of 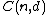 iff
iff
any two elements in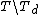 are separated by an even number of elements from
are separated by an even number of elements from 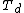 in the sequence
in the sequence 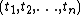 .
.
Convex polytope
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...
formed as a convex hull of n distinct points on a rational normal curve in Rd, where n is greater than d. These polytopes were studied by Constantin Carathéodory
Constantin Carathéodory
Constantin Carathéodory was a Greek mathematician. He made significant contributions to the theory of functions of a real variable, the calculus of variations, and measure theory...
, David Gale
David Gale
David Gale was a distinguished American mathematician and economist. He was a Professor Emeritus at University of California, Berkeley, affiliated with departments of Mathematics, Economics, and Industrial Engineering and Operations Research...
, Theodore Motzkin
Theodore Motzkin
Theodore Samuel Motzkin was an Israeli-American mathematician.- Biography :Motzkin's father, Leo Motzkin, was a noted Russian Zionist leader.Motzkin received his Ph.D...
, Victor Klee
Victor Klee
Victor L. Klee, Jr. was a mathematician specialising in convex sets, functional analysis, analysis of algorithms, optimization, and combinatorics. He spent almost his entire career at the University of Washington in Seattle.Born in San Francisco, Vic Klee earned his B.A...
, and others. They play an important role in polyhedral combinatorics
Polyhedral combinatorics
Polyhedral combinatorics is a branch of mathematics, within combinatorics and discrete geometry, that studies the problems of counting and describing the faces of convex polyhedra and higher dimensional convex polytopes....
: according to the Upper Bound Conjecture, proved by Peter McMullen and Richard Stanley
Richard P. Stanley
Richard Peter Stanley is the Norman Levinson Professor of Applied Mathematics at the Massachusetts Institute of Technology, in Cambridge, Massachusetts. He received his Ph.D. at Harvard University in 1971 under the supervision of Gian-Carlo Rota...
, the boundary Δ(n,d) of the cyclic polytope C(n,d) maximizes the number fi of i-dimensional faces among all simplicial spheres of dimension d − 1 with n vertices.
Definition
The moment curve in is defined by
is defined by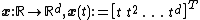 .
.The
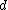 -dimensional cyclic polytope
-dimensional cyclic polytopeCyclic polytope
In mathematics, a cyclic polytope, denoted C, is a convex polytope formed as a convex hull of n distinct points on a rational normal curve in Rd, where n is greater than d. These polytopes were studied by Constantin Carathéodory, David Gale, Theodore Motzkin, Victor Klee, and others...
with
 vertices is the convex hull
vertices is the convex hullConvex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....

of
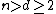 distinct points
distinct points 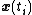 with
with 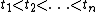 on the moment curve.
on the moment curve.The combinatorial structure of this polytope is independent of the points chosen, and the resulting polytope has dimension d and n vertices. Its boundary is a (d − 1)-dimensional simplicial polytope
Simplicial polytope
In geometry, a simplicial polytope is a d-polytope whose facets are all simplices.For example, a simplicial polyhedron contains only triangular faces and corresponds via Steinitz's theorem to a maximal planar graph....
denoted Δ(n,d).
Gale evenness condition
The Gale evenness condition provides a necessary and sufficient condition to determine a facet on a cyclic polytopeCyclic polytope
In mathematics, a cyclic polytope, denoted C, is a convex polytope formed as a convex hull of n distinct points on a rational normal curve in Rd, where n is greater than d. These polytopes were studied by Constantin Carathéodory, David Gale, Theodore Motzkin, Victor Klee, and others...
.
Let
 . Then, a
. Then, a  -subset
-subset 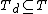 forms a facet of
forms a facet of 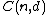 iff
iffIFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
any two elements in
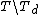 are separated by an even number of elements from
are separated by an even number of elements from 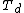 in the sequence
in the sequence 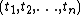 .
.The upper bound conjecture
The number of i-dimensional faces of Δ(n,d) is given by the formula-
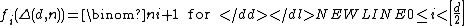
and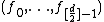 completely determine
completely determine 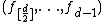 via the Dehn–Sommerville equations.
via the Dehn–Sommerville equations.
The Upper Bound Conjecture states that if Δ is a simplicial sphere of dimension d − 1 with n vertices , then
The Upper Bound Conjecture for simplicial polytopes was proposed by Motzkin in 1957 and proved by McMullen in 1970. A key ingredient in his proof was the following reformulation in terms of h-vectorsH-vectorIn algebraic combinatorics, the h-vector of a simplicial polytope is a fundamental invariant of the polytope which encodes the number of faces of different dimensions and allows one to express the Dehn–Sommerville equations in a particularly simple form...
:
-
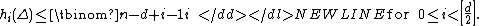
Victor Klee suggested that the same statement should hold for all simplicial spheres and this was indeed established in 1975 by Stanley using the notion of a Stanley–Reisner ring and homological methods
-


