
Gömböc
Encyclopedia
A gömböc is a convex three-dimensional homogeneous body which, when resting on a flat surface, has just one stable and one unstable point of equilibrium
. Its existence was conjectured by Russian mathematician Vladimir Arnold
in 1995 and proven in 2006 by Hungarian scientists Gábor Domokos and Péter Várkonyi. The gömböc shape is not unique; it has countless varieties, most of which are very close to a sphere and all have very strict shape tolerance (about 0.1 mm per 10 cm). The most famous solution has a sharpened top and is shown on the right. Its shape helped to explain the body structure of some turtle
s in relation to their ability to return to equilibrium position after being placed upside down. Copies of gömböcs have been donated to institutions and museums, and the biggest one was presented at the World Expo 2010 in Shanghai
, China
.
, a body with a single stable resting position is called monostatic, and the term mono-monostatic has been coined to describe a body which additionally has only one unstable point of balance. (The previously known monostatic polyhedron
does not qualify, as it has three unstable equilibria.) A sphere
weighted so that its center of mass
is shifted from the geometrical center is a mono-monostatic body. A more common example is the Comeback Kid, Weeble
or roly-poly toy
(see left figure). Not only does it have a low center of mass, but it also has a specific shape. At equilibrium, the center of mass and the contact point are on the line perpendicular to the ground. When the toy is pushed, its center of mass rises and also shifts away from that line. This produces a righting moment which returns the toy to the equilibrium position.
The above examples of mono-monostatic objects are necessarily inhomogeneous, that is, the density of their material varies across their body. The question of whether it is possible to construct a three-dimensional body which is mono-monostatic but also homogeneous and convex
was raised by Russian mathematician Vladimir Arnold
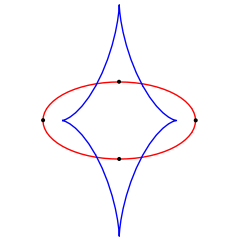
in 1995. The requirement of being convex is essential as it is trivial to construct a mono-monostatic non-convex body. Convex means that any straight line between two points on a body lies inside the body, or, in other words, that the surface has no sunken regions but instead bulges outward (or is at least flat) at every point. It was already well known, from a geometrical and topological generalization of the classical four-vertex theorem
, that a plane curve has at least four extrema of curvature, specifically, at least two local maxima and at least two local minima (see right figure), meaning that a (convex) mono-monostatic object does not exist in two dimensions. Whereas a common anticipation was that a three-dimensional body should also have at least four extrema, Arnold conjectured that this number could be smaller.
 The problem was solved in 2006 by Gábor Domokos and Péter Várkonyi. Domokos is an engineer and is the head of Mechanics, Materials and Structures at Budapest University of Technology and Economics
The problem was solved in 2006 by Gábor Domokos and Péter Várkonyi. Domokos is an engineer and is the head of Mechanics, Materials and Structures at Budapest University of Technology and Economics
. Since 2004, he is the youngest member of the Hungarian Academy of Sciences
. Várkonyi was trained as an architect; he was a student of Domokos and a silver medalist at the International Physics Olympiad
in 1997. After staying as a post-doctoral student at Princeton University
in 2006–2007, he assumed an assistant professor position at Budapest University of Technology and Economics
. Domokos had previously been working on mono-monostatic bodies. In 1995 he met Arnold at a major mathematics conference in Hamburg, where Arnold presented a plenary talk illustrating that most geometrical problems have four solutions or extremal points. In a personal discussion, however, Arnold questioned that four is a requirement for mono-monostatic bodies and encouraged Domokos to seek examples with fewer equilibria.
The rigorous proof of the solution can be found in references of their work. The summary of the results is that the three-dimensional homogeneous convex (mono-monostatic) body, which has one stable and one unstable equilibrium point, does exist and is not unique. Such bodies are hard to visualize, describe or identify. Their form is dissimilar to any typical representative of any other equilibrium geometrical class. They should have minimal "flatness", and, to avoid having two unstable equilibria, must also have minimal "thinness". They are the only non-degenerate
objects having simultaneously minimal flatness and thinness. The shape of those bodies is very sensitive to small variation, outside which it is no longer mono-monostatic. For example, the first solution of Domokos and Várkonyi closely resembled a sphere, with a shape deviation of only 10−5. It was dismissed, as it was extremely hard to test experimentally. Their published solution was less sensitive; yet it has a shape tolerance of 10−4, that is 0.1 mm for a 10 cm size.
Domokos and his wife developed a classification system for shapes based on their points of equilibrium by analyzing pebbles and noting their equilibrium points. In one experiment, they tried 2000 pebbles collected at the beaches of Rhodes
island and found no single mono-monostatic body among them, illustrating the difficulty to find or construct such a body.
The solution of Domokos and Várkonyi has curved edges and resembles a sphere with a squashed top. In the top figure, it rests in its stable equilibrium. Its unstable equilibrium position is obtained by rotating the figure 180° about a horizontal axis. Theoretically, it will rest there, but the smallest perturbation will bring it back to the stable point. The mathematical gömböc has indeed sphere-like properties. In particular its flatness and thinness are minimal, and this is the only type of nondegenerate object with this property. Domokos and Várkonyi are interested to find a polyhedral solution with the surface consisting of a minimal number of flat planes. Therefore, they offer a prize to anyone who finds such solution, which amounts to $10,000 divided by the number of planes in the solution. Obviously, one can approximate their curvilinear gömböc with a finite number of discrete surfaces, however, their estimate is it will take thousands of planes to achieve that. They hope, by offering this prize, to stimulate finding a radically different solution from their own.
). Originally gömböc is a sausage-like food: seasoned pork filled in pig-stomach. There is a Hungarian folk tale about an anthropomorphic gömböc, which swallows several people whole.
Domokos and Várkonyi spent a year measuring turtles in the Budapest Zoo, Hungarian Museum of Natural History and various pet shops in Budapest, digitizing and analyzing their shells, and attempting to "explain" their body shapes and functions from their geometry work. Their first biology paper was rejected 5 times, but finally accepted by the biology journal Proceedings of the Royal Society
. It was then immediately popularized in several science news reports, including those of the most prestigious science journals Nature
and Science
. The reported model can be summarized as flat shells in turtles are advantageous for swimming and digging. However, the sharp shell edges hinder the rolling. Those turtles usually have long legs and neck and actively use them to push the ground, in order to return to the normal position if placed upside down. On the contrary, more "round" turtles easily roll on their own; those have shorter limbs and use them little when recovering lost balance. (Some limb movement would always be needed because of imperfect shell shape, ground conditions, etc.) Round shells also resist better the crushing jaws of a predator and are better for thermal regulation.
 The explanation of turtle body shape, using the gömböc theory, has already been accepted by some biologists. For example, Robert McNeill Alexander, one of the pioneers of modern biomechanics
The explanation of turtle body shape, using the gömböc theory, has already been accepted by some biologists. For example, Robert McNeill Alexander, one of the pioneers of modern biomechanics
, used it in his plenary lecture on optimization in evolution in 2008.
No other practical applications of gömböcs are known, probably because a gömböc is an exotic solution for an idealized case of homogeneous solid – although balance recovery is crucial in such areas as robotics, it is typically achieved simply by making the bottom parts heavier.
technology. Its accuracy however was below requirements, and the gömböc would often get stuck in an intermediate position rather than returning to the stable equilibrium. The technology was improved to increase the spatial accuracy to the required 10−4 level and to use various construction materials. In particular, transparent (especially lightly colored) solids are visually appealing, as they demonstrate the homogeneous composition. Current materials for gömböcs include aluminium alloy (AlMgSi), brass
, Plexiglass and marble
. The balancing properties of a gömböc are affected by mechanical defects and dust both on its body and on the surface on which it rests. If damaged, the process of restoring the original shape is more complex than producing a new one. Although in theory the balancing properties should not depend on the material and object size, in practice, both larger and heavier gömböcs have better chances to return to equilibrium in case of defects.
Gömböc 1 was a gift to Vladimir Arnold on occasion of his 70th birthday. The largest gömböc is about 3 meters high and 3 meters wide. It was the major exhibit of the Hungarian pavilion at the World Expo 2010 in Shanghai
, China
.
when he designed his cube-shaped puzzle
in 1974. For their discovery, Domokos and Várkonyi were decorated with the Knight's Cross of the Republic of Hungary. The New York Times Magazine
selected the gömböc as one of the 70 most interesting ideas of the year 2007.
On February 13, 2009, a gömböc appeared on on BBC One
Friday night show QI
, where the host Stephen Fry
demonstrated its properties and Domokos, who was present in the audience, explained its history and relation to turtles.
The Stamp News website shows the new stamps issued on April 30, 2010 by Hungary which illustrate a gömböc in different positions. The stamp booklets are arranged in such a manner that the gömböc appears to come to life when the booklet is flipped. The stamps were issued in association with the gömböc on display at the World Expo 2010 (May 1 to October 31). This was also covered by Linn's Stamp News
magazine.
Mechanical equilibrium
A standard definition of static equilibrium is:This is a strict definition, and often the term "static equilibrium" is used in a more relaxed manner interchangeably with "mechanical equilibrium", as defined next....
. Its existence was conjectured by Russian mathematician Vladimir Arnold
Vladimir Arnold
Vladimir Igorevich Arnold was a Soviet and Russian mathematician. While he is best known for the Kolmogorov–Arnold–Moser theorem regarding the stability of integrable Hamiltonian systems, he made important contributions in several areas including dynamical systems theory, catastrophe theory,...
in 1995 and proven in 2006 by Hungarian scientists Gábor Domokos and Péter Várkonyi. The gömböc shape is not unique; it has countless varieties, most of which are very close to a sphere and all have very strict shape tolerance (about 0.1 mm per 10 cm). The most famous solution has a sharpened top and is shown on the right. Its shape helped to explain the body structure of some turtle
Turtle
Turtles are reptiles of the order Testudines , characterised by a special bony or cartilaginous shell developed from their ribs that acts as a shield...
s in relation to their ability to return to equilibrium position after being placed upside down. Copies of gömböcs have been donated to institutions and museums, and the biggest one was presented at the World Expo 2010 in Shanghai
Shanghai
Shanghai is the largest city by population in China and the largest city proper in the world. It is one of the four province-level municipalities in the People's Republic of China, with a total population of over 23 million as of 2010...
, China
People's Republic of China
China , officially the People's Republic of China , is the most populous country in the world, with over 1.3 billion citizens. Located in East Asia, the country covers approximately 9.6 million square kilometres...
.
History
In geometryGeometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a body with a single stable resting position is called monostatic, and the term mono-monostatic has been coined to describe a body which additionally has only one unstable point of balance. (The previously known monostatic polyhedron
Monostatic polytope
In geometry, a monostatic polytope is a d-polytope which "can stand on only one face". They were described in 1969 by J.H. Conway, M. Goldberg and R.K. Guy. The monostatic polytope in 3-space they constructed has only 19 faces, the record so far.- Definition :A polytope is called monostatic if,...
does not qualify, as it has three unstable equilibria.) A sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
weighted so that its center of mass
Center of mass
In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...
is shifted from the geometrical center is a mono-monostatic body. A more common example is the Comeback Kid, Weeble
Weeble
Weebles is a trademark for several lines of children's roly-poly toys originating in Hasbro's Playskool division on July 23, 1971. Tipping an egg-shaped Weeble causes a weight located at the bottom-center to be lifted off the ground...
or roly-poly toy
Roly-poly toy
A roly-poly toy, round-bottomed doll, tilting doll, tumbler or wobbly man is a toy that rights itself when pushed over. The bottom of a roly-poly toy is round, roughly a hemisphere. Many roly-poly toys are hollow, with a weight inside the bottom. It has a center of mass below the center of the...
(see left figure). Not only does it have a low center of mass, but it also has a specific shape. At equilibrium, the center of mass and the contact point are on the line perpendicular to the ground. When the toy is pushed, its center of mass rises and also shifts away from that line. This produces a righting moment which returns the toy to the equilibrium position.
The above examples of mono-monostatic objects are necessarily inhomogeneous, that is, the density of their material varies across their body. The question of whether it is possible to construct a three-dimensional body which is mono-monostatic but also homogeneous and convex
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
was raised by Russian mathematician Vladimir Arnold
Vladimir Arnold
Vladimir Igorevich Arnold was a Soviet and Russian mathematician. While he is best known for the Kolmogorov–Arnold–Moser theorem regarding the stability of integrable Hamiltonian systems, he made important contributions in several areas including dynamical systems theory, catastrophe theory,...
in 1995. The requirement of being convex is essential as it is trivial to construct a mono-monostatic non-convex body. Convex means that any straight line between two points on a body lies inside the body, or, in other words, that the surface has no sunken regions but instead bulges outward (or is at least flat) at every point. It was already well known, from a geometrical and topological generalization of the classical four-vertex theorem
Four-vertex theorem
The four-vertex theorem states that the curvature function of a simple, closed, smooth plane curve has at least four local extrema...
, that a plane curve has at least four extrema of curvature, specifically, at least two local maxima and at least two local minima (see right figure), meaning that a (convex) mono-monostatic object does not exist in two dimensions. Whereas a common anticipation was that a three-dimensional body should also have at least four extrema, Arnold conjectured that this number could be smaller.
Mathematical solution

Budapest University of Technology and Economics
The Budapest University of Technology and Economics , in hungarian abbreviated as BME, English official abbreviation BUTE, is the most significant University of Technology in Hungary and is also one of the oldest Institutes of Technology in the world, having been founded in 1782.-History:BME is...
. Since 2004, he is the youngest member of the Hungarian Academy of Sciences
Hungarian Academy of Sciences
The Hungarian Academy of Sciences is the most important and prestigious learned society of Hungary. Its seat is at the bank of the Danube in Budapest.-History:...
. Várkonyi was trained as an architect; he was a student of Domokos and a silver medalist at the International Physics Olympiad
International Physics Olympiad
The International Physics Olympiad is an annual physics competition for high school students. It is one of the International Science Olympiads. The first IPhO was held in Warsaw, Poland in 1967....
in 1997. After staying as a post-doctoral student at Princeton University
Princeton University
Princeton University is a private research university located in Princeton, New Jersey, United States. The school is one of the eight universities of the Ivy League, and is one of the nine Colonial Colleges founded before the American Revolution....
in 2006–2007, he assumed an assistant professor position at Budapest University of Technology and Economics
Budapest University of Technology and Economics
The Budapest University of Technology and Economics , in hungarian abbreviated as BME, English official abbreviation BUTE, is the most significant University of Technology in Hungary and is also one of the oldest Institutes of Technology in the world, having been founded in 1782.-History:BME is...
. Domokos had previously been working on mono-monostatic bodies. In 1995 he met Arnold at a major mathematics conference in Hamburg, where Arnold presented a plenary talk illustrating that most geometrical problems have four solutions or extremal points. In a personal discussion, however, Arnold questioned that four is a requirement for mono-monostatic bodies and encouraged Domokos to seek examples with fewer equilibria.
The rigorous proof of the solution can be found in references of their work. The summary of the results is that the three-dimensional homogeneous convex (mono-monostatic) body, which has one stable and one unstable equilibrium point, does exist and is not unique. Such bodies are hard to visualize, describe or identify. Their form is dissimilar to any typical representative of any other equilibrium geometrical class. They should have minimal "flatness", and, to avoid having two unstable equilibria, must also have minimal "thinness". They are the only non-degenerate
Degeneracy (mathematics)
In mathematics, a degenerate case is a limiting case in which a class of object changes its nature so as to belong to another, usually simpler, class....
objects having simultaneously minimal flatness and thinness. The shape of those bodies is very sensitive to small variation, outside which it is no longer mono-monostatic. For example, the first solution of Domokos and Várkonyi closely resembled a sphere, with a shape deviation of only 10−5. It was dismissed, as it was extremely hard to test experimentally. Their published solution was less sensitive; yet it has a shape tolerance of 10−4, that is 0.1 mm for a 10 cm size.
Domokos and his wife developed a classification system for shapes based on their points of equilibrium by analyzing pebbles and noting their equilibrium points. In one experiment, they tried 2000 pebbles collected at the beaches of Rhodes
Rhodes
Rhodes is an island in Greece, located in the eastern Aegean Sea. It is the largest of the Dodecanese islands in terms of both land area and population, with a population of 117,007, and also the island group's historical capital. Administratively the island forms a separate municipality within...
island and found no single mono-monostatic body among them, illustrating the difficulty to find or construct such a body.
The solution of Domokos and Várkonyi has curved edges and resembles a sphere with a squashed top. In the top figure, it rests in its stable equilibrium. Its unstable equilibrium position is obtained by rotating the figure 180° about a horizontal axis. Theoretically, it will rest there, but the smallest perturbation will bring it back to the stable point. The mathematical gömböc has indeed sphere-like properties. In particular its flatness and thinness are minimal, and this is the only type of nondegenerate object with this property. Domokos and Várkonyi are interested to find a polyhedral solution with the surface consisting of a minimal number of flat planes. Therefore, they offer a prize to anyone who finds such solution, which amounts to $10,000 divided by the number of planes in the solution. Obviously, one can approximate their curvilinear gömböc with a finite number of discrete surfaces, however, their estimate is it will take thousands of planes to achieve that. They hope, by offering this prize, to stimulate finding a radically different solution from their own.
Name
If analyzed quantitatively in terms of flatness and thickness, the discovered mono-monostatic body is the most sphere-like body, apart from the sphere itself. Because of this, it was named gömböc, meaning a diminutive of gömb ("sphere" in HungarianHungarian language
Hungarian is a Uralic language, part of the Ugric group. With some 14 million speakers, it is one of the most widely spoken non-Indo-European languages in Europe....
). Originally gömböc is a sausage-like food: seasoned pork filled in pig-stomach. There is a Hungarian folk tale about an anthropomorphic gömböc, which swallows several people whole.
Relation to animals
The balancing properties of the gömböc are associated with the "righting response", their ability to turn back when placed upside down, of shelled animals such as turtles and beetles. This may happen in a fight or predator attack and is crucial for their survival. The presence of only one stable and unstable point in a gömböc means that it would return to one equilibrium position no matter how it is pushed or turned around. Whereas relatively flat animals (such as beetles) heavily rely on momentum and thrust developed by moving their limbs and wings, the limbs of many dome-shaped turtles are too short to be of use in righting themselves.Domokos and Várkonyi spent a year measuring turtles in the Budapest Zoo, Hungarian Museum of Natural History and various pet shops in Budapest, digitizing and analyzing their shells, and attempting to "explain" their body shapes and functions from their geometry work. Their first biology paper was rejected 5 times, but finally accepted by the biology journal Proceedings of the Royal Society
Proceedings of the Royal Society
Proceedings of the Royal Society is the parent title of two scientific journals published by the Royal Society, whereas its initial journal, Philosophical Transactions, is now devoted to special thematic issues...
. It was then immediately popularized in several science news reports, including those of the most prestigious science journals Nature
Nature (journal)
Nature, first published on 4 November 1869, is ranked the world's most cited interdisciplinary scientific journal by the Science Edition of the 2010 Journal Citation Reports...
and Science
Science (journal)
Science is the academic journal of the American Association for the Advancement of Science and is one of the world's top scientific journals....
. The reported model can be summarized as flat shells in turtles are advantageous for swimming and digging. However, the sharp shell edges hinder the rolling. Those turtles usually have long legs and neck and actively use them to push the ground, in order to return to the normal position if placed upside down. On the contrary, more "round" turtles easily roll on their own; those have shorter limbs and use them little when recovering lost balance. (Some limb movement would always be needed because of imperfect shell shape, ground conditions, etc.) Round shells also resist better the crushing jaws of a predator and are better for thermal regulation.

Biomechanics
Biomechanics is the application of mechanical principles to biological systems, such as humans, animals, plants, organs, and cells. Perhaps one of the best definitions was provided by Herbert Hatze in 1974: "Biomechanics is the study of the structure and function of biological systems by means of...
, used it in his plenary lecture on optimization in evolution in 2008.
No other practical applications of gömböcs are known, probably because a gömböc is an exotic solution for an idealized case of homogeneous solid – although balance recovery is crucial in such areas as robotics, it is typically achieved simply by making the bottom parts heavier.
Production
The strict shape tolerance of gömböcs hindered production. The first prototype of a gömböc was manufactured in summer 2006 using three-dimensional Rapid PrototypingRapid prototyping
Rapid prototyping is the automatic construction of physical objects using additive manufacturing technology. The first techniques for rapid prototyping became available in the late 1980s and were used to produce models and prototype parts. Today, they are used for a much wider range of applications...
technology. Its accuracy however was below requirements, and the gömböc would often get stuck in an intermediate position rather than returning to the stable equilibrium. The technology was improved to increase the spatial accuracy to the required 10−4 level and to use various construction materials. In particular, transparent (especially lightly colored) solids are visually appealing, as they demonstrate the homogeneous composition. Current materials for gömböcs include aluminium alloy (AlMgSi), brass
Brass
Brass is an alloy of copper and zinc; the proportions of zinc and copper can be varied to create a range of brasses with varying properties.In comparison, bronze is principally an alloy of copper and tin...
, Plexiglass and marble
Marble
Marble is a metamorphic rock composed of recrystallized carbonate minerals, most commonly calcite or dolomite.Geologists use the term "marble" to refer to metamorphosed limestone; however stonemasons use the term more broadly to encompass unmetamorphosed limestone.Marble is commonly used for...
. The balancing properties of a gömböc are affected by mechanical defects and dust both on its body and on the surface on which it rests. If damaged, the process of restoring the original shape is more complex than producing a new one. Although in theory the balancing properties should not depend on the material and object size, in practice, both larger and heavier gömböcs have better chances to return to equilibrium in case of defects.
Gömböc 1 was a gift to Vladimir Arnold on occasion of his 70th birthday. The largest gömböc is about 3 meters high and 3 meters wide. It was the major exhibit of the Hungarian pavilion at the World Expo 2010 in Shanghai
Shanghai
Shanghai is the largest city by population in China and the largest city proper in the world. It is one of the four province-level municipalities in the People's Republic of China, with a total population of over 23 million as of 2010...
, China
People's Republic of China
China , officially the People's Republic of China , is the most populous country in the world, with over 1.3 billion citizens. Located in East Asia, the country covers approximately 9.6 million square kilometres...
.
Media
The invention of the gömböc has been in the focus of public and media attention, repeating the success of another Hungarian Ernő RubikErno Rubik
Ernő Rubik is a Hungarian inventor, architect and professor of architecture. He is best known for the invention of mechanical puzzles including Rubik's Cube , Rubik's Magic, Rubik's Magic: Master Edition, Rubik's Snake and Rubik's 360....
when he designed his cube-shaped puzzle
Rubik's Cube
Rubik's Cube is a 3-D mechanical puzzle invented in 1974 by Hungarian sculptor and professor of architecture Ernő Rubik.Originally called the "Magic Cube", the puzzle was licensed by Rubik to be sold by Ideal Toy Corp. in 1980 and won the German Game of the Year special award for Best Puzzle that...
in 1974. For their discovery, Domokos and Várkonyi were decorated with the Knight's Cross of the Republic of Hungary. The New York Times Magazine
The New York Times Magazine
The New York Times Magazine is a Sunday magazine supplement included with the Sunday edition of The New York Times. It is host to feature articles longer than those typically in the newspaper and has attracted many notable contributors...
selected the gömböc as one of the 70 most interesting ideas of the year 2007.
On February 13, 2009, a gömböc appeared on on BBC One
BBC One
BBC One is the flagship television channel of the British Broadcasting Corporation in the United Kingdom. It was launched on 2 November 1936 as the BBC Television Service, and was the world's first regular television service with a high level of image resolution...
Friday night show QI
QI
QI is a British comedy panel game television quiz show created and co-produced by John Lloyd, hosted by Stephen Fry, and featuring permanent panellist Alan Davies. Most of the questions are extremely obscure, making it unlikely that the correct answer will be given...
, where the host Stephen Fry
Stephen Fry
Stephen John Fry is an English actor, screenwriter, author, playwright, journalist, poet, comedian, television presenter and film director, and a director of Norwich City Football Club. He first came to attention in the 1981 Cambridge Footlights Revue presentation "The Cellar Tapes", which also...
demonstrated its properties and Domokos, who was present in the audience, explained its history and relation to turtles.
The Stamp News website shows the new stamps issued on April 30, 2010 by Hungary which illustrate a gömböc in different positions. The stamp booklets are arranged in such a manner that the gömböc appears to come to life when the booklet is flipped. The stamps were issued in association with the gömböc on display at the World Expo 2010 (May 1 to October 31). This was also covered by Linn's Stamp News
Linn's Stamp News
Linn's Stamp News an American publication, is the largest weekly newspaper for stamp collectors, with a paid circulation of just over 46,000 Circulation peaked at almost 92,000 in 1978 and has declined ever since because fewer new collectors are subscribing to replace those who subscribed in the...
magazine.

