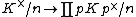Grunwald–Wang theorem
Encyclopedia
In algebraic number theory
, the Grunwald–Wang theorem states that—except in some precisely defined exceptional cases—an element x in a number field K is an nth power in K if it is an nth power in the localization
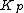 for almost all
for almost all
(i.e. all but finitely many) primes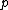 of K. For example, a rational number
of K. For example, a rational number
is a square of a rational number if it is a square of a p-adic number
for almost all primes p. The Grunwald–Wang theorem is an example of a local-global principle.
It was introduced by , but there was a mistake in this original version that was found and corrected by .
, "proved" the erroneous statement that an element in a number field is an nth power if it is an nth power locally almost everywhere. gave another "proof" of this incorrect statement. However discovered the following counter-example: 16 is a p-adic 8th power for all odd primes p, but not a rational (or 2-adic) 8th power. In his doctoral thesis written under Artin
, Wang gave and proved the correct formulation of Grunwald's theorem. This result is what is now known as the Grunwald–Wang theorem. The history of Wang's counterexample is discussed in
Generally, 16 is an 8th power in a field K if and only if the polynomial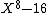 has a root in K. Write
has a root in K. Write
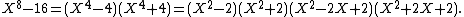
Thus, 16 is an 8th power in K if and only if 2, −2 or −1 is a square in K. Let p be any odd prime. It follows from the multiplicativity of the Legendre symbol
that 2, −2 or −1 is a square modulo p. Hence, by Hensel's lemma
, 2, −2 or −1 is a square in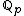 .
.
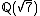 although it is an 8th power locally everywhere (i.e. in
although it is an 8th power locally everywhere (i.e. in 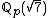 for all p). This follows from the above and the equality
for all p). This follows from the above and the equality 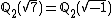 .
.
There exists no cyclic degree 8 extension in which the prime 2 is totally inert (i.e. such that
in which the prime 2 is totally inert (i.e. such that  has degree 8).
has degree 8).
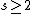 let
let
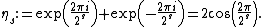
Note that the th cyclotomic field
th cyclotomic field
is
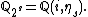
A field is called s-special if it contains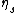 , but neither
, but neither 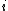 ,
, 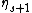 nor
nor 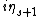 .
.
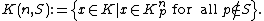
The Grunwald–Wang theorem says that
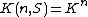
unless we are in the special case which occurs when the following two conditions both hold:
The failure of the Hasse principle is finite: In the special case, the kernel of
is Z/2.
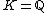 is 2-special since it contains
is 2-special since it contains 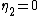 , but neither
, but neither 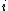 ,
,  nor
nor 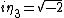 . The special set is
. The special set is 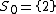 . Thus, the special case in the Grunwald–Wang theorem occurs when n is divisible by 8, and S contains 2. This explains Wang's counter-example and shows that it is minimal. It is also seen that an element in
. Thus, the special case in the Grunwald–Wang theorem occurs when n is divisible by 8, and S contains 2. This explains Wang's counter-example and shows that it is minimal. It is also seen that an element in 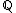 is an nth power if it is a p-adic nth power for all p.
is an nth power if it is a p-adic nth power for all p.
The field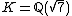 is 2-special as well, but with
is 2-special as well, but with 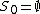 . This explains the other counter-example above.
. This explains the other counter-example above.
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
, the Grunwald–Wang theorem states that—except in some precisely defined exceptional cases—an element x in a number field K is an nth power in K if it is an nth power in the localization
Localization of a ring
In abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
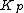 for almost all
for almost allAlmost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
(i.e. all but finitely many) primes
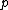 of K. For example, a rational number
of K. For example, a rational numberRational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
is a square of a rational number if it is a square of a p-adic number
P-adic number
In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
for almost all primes p. The Grunwald–Wang theorem is an example of a local-global principle.
It was introduced by , but there was a mistake in this original version that was found and corrected by .
History
, a student of HasseHelmut Hasse
Helmut Hasse was a German mathematician working in algebraic number theory, known for fundamental contributions to class field theory, the application of p-adic numbers to local classfield theory and diophantine geometry , and to local zeta functions.-Life:He was born in Kassel, and died in...
, "proved" the erroneous statement that an element in a number field is an nth power if it is an nth power locally almost everywhere. gave another "proof" of this incorrect statement. However discovered the following counter-example: 16 is a p-adic 8th power for all odd primes p, but not a rational (or 2-adic) 8th power. In his doctoral thesis written under Artin
Emil Artin
Emil Artin was an Austrian-American mathematician of Armenian descent.-Parents:Emil Artin was born in Vienna to parents Emma Maria, née Laura , a soubrette on the operetta stages of Austria and Germany, and Emil Hadochadus Maria Artin, Austrian-born of Armenian descent...
, Wang gave and proved the correct formulation of Grunwald's theorem. This result is what is now known as the Grunwald–Wang theorem. The history of Wang's counterexample is discussed in
Proof of Wang's counter-example
It is clear that 16 is not a 2-adic 8th power, and hence not a rational 8th power, since the 2-adic valuation of 16 is 4 which is not divisible by 8.Generally, 16 is an 8th power in a field K if and only if the polynomial
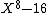 has a root in K. Write
has a root in K. Write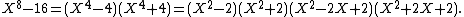
Thus, 16 is an 8th power in K if and only if 2, −2 or −1 is a square in K. Let p be any odd prime. It follows from the multiplicativity of the Legendre symbol
Legendre symbol
In number theory, the Legendre symbol is a multiplicative function with values 1, −1, 0 that is a quadratic character modulo a prime number p: its value on a quadratic residue mod p is 1 and on a quadratic non-residue is −1....
that 2, −2 or −1 is a square modulo p. Hence, by Hensel's lemma
Hensel's lemma
In mathematics, Hensel's lemma, also known as Hensel's lifting lemma, named after Kurt Hensel, is a result in modular arithmetic, stating that if a polynomial equation has a simple root modulo a prime number , then this root corresponds to a unique root of the same equation modulo any higher power...
, 2, −2 or −1 is a square in
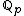 .
.Another counter-example
16 is not an 8th power in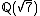 although it is an 8th power locally everywhere (i.e. in
although it is an 8th power locally everywhere (i.e. in 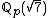 for all p). This follows from the above and the equality
for all p). This follows from the above and the equality 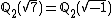 .
.A consequence of Wang's counter-example
Wang's counter-example has the following interesting consequence showing that one cannot always find a cyclic Galois extension of a given degree of a number field in which finitely many given prime places split in a specified way:There exists no cyclic degree 8 extension
 in which the prime 2 is totally inert (i.e. such that
in which the prime 2 is totally inert (i.e. such that  has degree 8).
has degree 8).Special fields
For any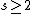 let
let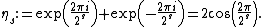
Note that the
 th cyclotomic field
th cyclotomic fieldCyclotomic field
In number theory, a cyclotomic field is a number field obtained by adjoining a complex primitive root of unity to Q, the field of rational numbers...
is
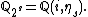
A field is called s-special if it contains
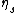 , but neither
, but neither 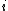 ,
, 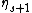 nor
nor 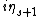 .
.Statement of the theorem
Consider a number field K and a natural number n. Let S be a finite (possibly empty) set of primes of K and put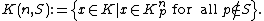
The Grunwald–Wang theorem says that
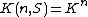
unless we are in the special case which occurs when the following two conditions both hold:
-
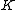 is s-special with an
is s-special with an  such that
such that 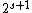 divides n.
divides n. -
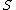 contains the special set
contains the special set 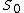 consisting of those (necessarily 2-adic) primes
consisting of those (necessarily 2-adic) primes 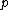 such that
such that 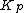 is s-special.
is s-special.
The failure of the Hasse principle is finite: In the special case, the kernel of
is Z/2.
Explanation of Wang's counter-example
The field of rational numbers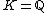 is 2-special since it contains
is 2-special since it contains 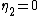 , but neither
, but neither 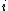 ,
,  nor
nor 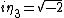 . The special set is
. The special set is 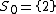 . Thus, the special case in the Grunwald–Wang theorem occurs when n is divisible by 8, and S contains 2. This explains Wang's counter-example and shows that it is minimal. It is also seen that an element in
. Thus, the special case in the Grunwald–Wang theorem occurs when n is divisible by 8, and S contains 2. This explains Wang's counter-example and shows that it is minimal. It is also seen that an element in 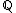 is an nth power if it is a p-adic nth power for all p.
is an nth power if it is a p-adic nth power for all p.The field
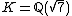 is 2-special as well, but with
is 2-special as well, but with 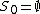 . This explains the other counter-example above.
. This explains the other counter-example above.