
Gross-Pitaevskii equation
Encyclopedia
The Gross–Pitaevskii equation (named after Eugene P. Gross and Lev Petrovich Pitaevskii) describes the ground state of a quantum system of identical boson
s using the Hartree–Fock approximation and the pseudopotential
interaction model.
In the Hartree–Fock approximation the total wave-function
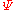 of the system of
of the system of  bosons is taken as a product of single-particle functions
bosons is taken as a product of single-particle functions 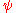 ,
,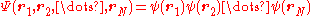
where is the coordinate of the
is the coordinate of the 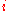 -th boson.
-th boson.
The pseudopotential model Hamiltonian of the system is given as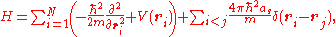
where is the mass of the boson,
is the mass of the boson,  is the external potential,
is the external potential,  is the boson-boson scattering length, and
is the boson-boson scattering length, and 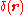 is the Dirac delta-function.
is the Dirac delta-function.
If the single-particle wave-function satisfies the Gross–Pitaevski equation,
the total wave-function minimizes the expectation value of the model Hamiltonian under normalization condition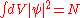 .
.
It is a model equation for the single-particle wavefunction
in a Bose–Einstein condensate
. It is similar in form to the Ginzburg–Landau equation and is sometimes referred to as a nonlinear Schrödinger equation
.
A Bose–Einstein condensate
(BEC) is a gas of bosons that are in the same quantum state, and thus can be described by the same wavefunction
. A free quantum particle is described by a single-particle Schrödinger equation
. Interaction between particles in a real gas is taken into account by a pertinent many-body Schrödinger equation. If the average spacing between the particles in a gas is greater than the scattering length (that is, in the so-called dilute limit), then one can approximate the true interaction potential that features in this equation by a pseudopotential
. The non-linearity of the Gross–Pitaevskii equation has its origin in the interaction between the particles. This becomes evident by equating the coupling constant of interaction in the Gross–Pitaevskii equation with zero (see the following section), on which the single-particle Schrödinger equation describing a particle inside a trapping potential is recovered.
with the addition of an interaction term. The coupling constant, g, is proportional to the scattering length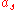 of two interacting bosons:
of two interacting bosons:
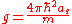 ,
,
where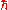 is Planck's constant and m is the mass of the boson.
is Planck's constant and m is the mass of the boson.
The energy density
is

where is the wavefunction, or order parameter, and V is an external potential.
is the wavefunction, or order parameter, and V is an external potential.
The time-independent Gross–Pitaevskii equation, for a conserved number of particles, is

where is the chemical potential
is the chemical potential
. The chemical potential
is found from the condition that the number of particles is related to the wavefunction
by
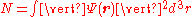 .
.
From the time-independent Gross–Pitaevskii equation, we can find the structure of a Bose–Einstein condensate in various external potentials (e.g. a harmonic trap).
The time-dependent Gross–Pitaevskii equation is
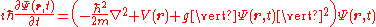 .
.
From the time-dependent Gross–Pitaevskii equation we can look at the dynamics of the Bose–Einstein condensate. It is used to find the collective modes of a trapped gas.
, exact solutions are hard to come by. As a result, solutions have to be approximated via myriad techniques.
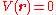 ,
,
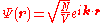 .
.
This solution is often called the Hartree solution. Although it does satisfy the Gross–Pitaevskii equation, it leaves a gap in the energy spectrum due to the interaction:
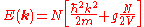 .
.
According to the Hugenholtz–Pines theorem, an interacting bose gas does not exhibit an energy gap (in the case of repulsive interactions).
can form in a Bose–Einstein condensate, and depending upon whether the interaction is attractive or repulsive, there is either a light or dark soliton. Both solitons are local disturbances in a condensate with a uniform background density
If the BEC is repulsive, so that , then a possible solution of the Gross–Pitaevskii equation is,
, then a possible solution of the Gross–Pitaevskii equation is,
 ,
,
where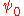 is the value of the condensate wavefunction at
is the value of the condensate wavefunction at  , and
, and 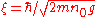 , is the coherence length. This solution represents the dark soliton, since there is a deficit of condensate in a space of nonzero density. The dark soliton is also a type of topological defect
, is the coherence length. This solution represents the dark soliton, since there is a deficit of condensate in a space of nonzero density. The dark soliton is also a type of topological defect
, since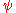 flips between positive and negative values across the origin, corresponding to a
flips between positive and negative values across the origin, corresponding to a  phase shift.
phase shift.
For
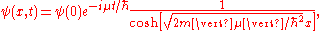
where the chemical potential is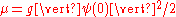 . This solution represents the bright soliton, since there is a concentration of condensate in a space of zero density.
. This solution represents the bright soliton, since there is a concentration of condensate in a space of zero density.
for the wavefunction with free parameters, plug it into the free energy, and minimize the energy with respect to the free parameters.
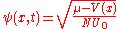
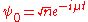 and a small perturbation
and a small perturbation 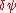
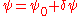
Then this form is inserted in the time dependent Gross–Pitaevskii equation and its complex conjugate, and linearized to first order in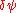

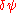
Assuming the following for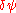
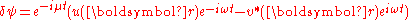
one finds the following coupled differential equations for and
and 
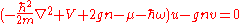
For a homogenous system, i.e. for , one can assume
, one can assume  and
and  to be plane waves of momentum
to be plane waves of momentum 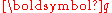 , which leads to the energy spectrum
, which leads to the energy spectrum

For large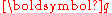 , the dispersion relation is quadratic in
, the dispersion relation is quadratic in 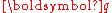 as one would expect for usual non interacting single particle excitations. For small
as one would expect for usual non interacting single particle excitations. For small 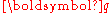 , the dispersion relation is linear
, the dispersion relation is linear

with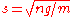 being the speed of sound in the condensate. The fact that
being the speed of sound in the condensate. The fact that  shows, according to Landau's criterion, that the condensate is a superfluid, meaning that if an object is moved in the condensate at a velocity inferior to s, it will not be energetically favorable to produce excitations and the object will move without dissipation, which is a characteristic of a superfluid
shows, according to Landau's criterion, that the condensate is a superfluid, meaning that if an object is moved in the condensate at a velocity inferior to s, it will not be energetically favorable to produce excitations and the object will move without dissipation, which is a characteristic of a superfluid
. Experiments have been done to prove this superfluidity of the condensate, using a tightly focused blue-detuned laser .
The same dispersion relation is found when the condensate is described from a microscopical approach using the formalism of second quantization.
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
s using the Hartree–Fock approximation and the pseudopotential
Pseudopotential
In physics, a pseudopotential or effective potential is used as an approximation for the simplified description of complex systems. Applications include atomic physics and neutron scattering.- Atomic physics :...
interaction model.
In the Hartree–Fock approximation the total wave-function
Wavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
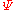 of the system of
of the system of  bosons is taken as a product of single-particle functions
bosons is taken as a product of single-particle functions 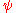 ,
,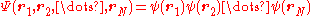
where
 is the coordinate of the
is the coordinate of the 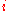 -th boson.
-th boson.The pseudopotential model Hamiltonian of the system is given as
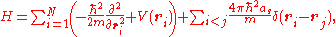
where
 is the mass of the boson,
is the mass of the boson,  is the external potential,
is the external potential,  is the boson-boson scattering length, and
is the boson-boson scattering length, and 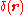 is the Dirac delta-function.
is the Dirac delta-function.If the single-particle wave-function satisfies the Gross–Pitaevski equation,

the total wave-function minimizes the expectation value of the model Hamiltonian under normalization condition
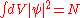 .
.It is a model equation for the single-particle wavefunction
Wavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
in a Bose–Einstein condensate
Bose–Einstein condensate
A Bose–Einstein condensate is a state of matter of a dilute gas of weakly interacting bosons confined in an external potential and cooled to temperatures very near absolute zero . Under such conditions, a large fraction of the bosons occupy the lowest quantum state of the external potential, at...
. It is similar in form to the Ginzburg–Landau equation and is sometimes referred to as a nonlinear Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
.
A Bose–Einstein condensate
Bose–Einstein condensate
A Bose–Einstein condensate is a state of matter of a dilute gas of weakly interacting bosons confined in an external potential and cooled to temperatures very near absolute zero . Under such conditions, a large fraction of the bosons occupy the lowest quantum state of the external potential, at...
(BEC) is a gas of bosons that are in the same quantum state, and thus can be described by the same wavefunction
Wavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
. A free quantum particle is described by a single-particle Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
. Interaction between particles in a real gas is taken into account by a pertinent many-body Schrödinger equation. If the average spacing between the particles in a gas is greater than the scattering length (that is, in the so-called dilute limit), then one can approximate the true interaction potential that features in this equation by a pseudopotential
Pseudopotential
In physics, a pseudopotential or effective potential is used as an approximation for the simplified description of complex systems. Applications include atomic physics and neutron scattering.- Atomic physics :...
. The non-linearity of the Gross–Pitaevskii equation has its origin in the interaction between the particles. This becomes evident by equating the coupling constant of interaction in the Gross–Pitaevskii equation with zero (see the following section), on which the single-particle Schrödinger equation describing a particle inside a trapping potential is recovered.
Form of equation
The equation has the form of the Schrödinger equationSchrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
with the addition of an interaction term. The coupling constant, g, is proportional to the scattering length
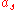 of two interacting bosons:
of two interacting bosons: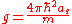 ,
,where
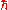 is Planck's constant and m is the mass of the boson.
is Planck's constant and m is the mass of the boson.The energy density
Energy density
Energy density is a term used for the amount of energy stored in a given system or region of space per unit volume. Often only the useful or extractable energy is quantified, which is to say that chemically inaccessible energy such as rest mass energy is ignored...
is

where
 is the wavefunction, or order parameter, and V is an external potential.
is the wavefunction, or order parameter, and V is an external potential.The time-independent Gross–Pitaevskii equation, for a conserved number of particles, is

where
 is the chemical potential
is the chemical potentialChemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
. The chemical potential
Chemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
is found from the condition that the number of particles is related to the wavefunction
Wavefunction
Not to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
by
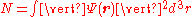 .
.From the time-independent Gross–Pitaevskii equation, we can find the structure of a Bose–Einstein condensate in various external potentials (e.g. a harmonic trap).
The time-dependent Gross–Pitaevskii equation is
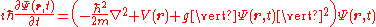 .
.From the time-dependent Gross–Pitaevskii equation we can look at the dynamics of the Bose–Einstein condensate. It is used to find the collective modes of a trapped gas.
Solutions
Since the Gross–Pitaevskii equation is a nonlinear, partial differential equationPartial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
, exact solutions are hard to come by. As a result, solutions have to be approximated via myriad techniques.
Free particle
The simplest exact solution is the free particle solution, with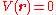 ,
,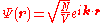 .
.This solution is often called the Hartree solution. Although it does satisfy the Gross–Pitaevskii equation, it leaves a gap in the energy spectrum due to the interaction:
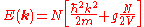 .
.According to the Hugenholtz–Pines theorem, an interacting bose gas does not exhibit an energy gap (in the case of repulsive interactions).
Soliton
A one-dimensional solitonSoliton
In mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium...
can form in a Bose–Einstein condensate, and depending upon whether the interaction is attractive or repulsive, there is either a light or dark soliton. Both solitons are local disturbances in a condensate with a uniform background density
If the BEC is repulsive, so that
 , then a possible solution of the Gross–Pitaevskii equation is,
, then a possible solution of the Gross–Pitaevskii equation is, ,
,where
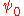 is the value of the condensate wavefunction at
is the value of the condensate wavefunction at  , and
, and 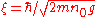 , is the coherence length. This solution represents the dark soliton, since there is a deficit of condensate in a space of nonzero density. The dark soliton is also a type of topological defect
, is the coherence length. This solution represents the dark soliton, since there is a deficit of condensate in a space of nonzero density. The dark soliton is also a type of topological defectTopological defect
In mathematics and physics, a topological soliton or a topological defect is a solution of a system of partial differential equations or of a quantum field theory homotopically distinct from the vacuum solution; it can be proven to exist because the boundary conditions entail the existence of...
, since
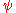 flips between positive and negative values across the origin, corresponding to a
flips between positive and negative values across the origin, corresponding to a  phase shift.
phase shift.For

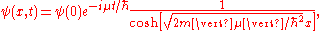
where the chemical potential is
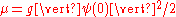 . This solution represents the bright soliton, since there is a concentration of condensate in a space of zero density.
. This solution represents the bright soliton, since there is a concentration of condensate in a space of zero density.Variational solutions
In systems where an exact analytical solution may not be feasible, one can make a variational approximation. The basic idea is to make a variational ansatzAnsatz
Ansatz is a German noun with several meanings in the English language.It is widely encountered in physics and mathematics literature.Since ansatz is a noun, in German texts the initial a of this word is always capitalised.-Definition:...
for the wavefunction with free parameters, plug it into the free energy, and minimize the energy with respect to the free parameters.
Thomas–Fermi approximation
If the number of particles in a gas is very large, the interatomic interaction becomes large so that the kinetic energy term can be neglected from the Gross–Pitaevskii equation. This is called the Thomas–Fermi approximation.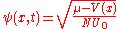
Bogoliubov approximation
Bogoliubov treatment of the Gross–Pitaevskii equation is a method that finds the elementary excitations of a Bose-Einstein condensate. To that purpose, the condensate wavefunction is approximated by a sum of the equilibrium wavefunction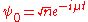 and a small perturbation
and a small perturbation 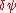
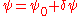
Then this form is inserted in the time dependent Gross–Pitaevskii equation and its complex conjugate, and linearized to first order in
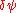

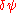
Assuming the following for
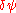
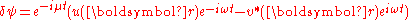
one finds the following coupled differential equations for
 and
and 
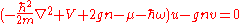
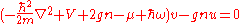
For a homogenous system, i.e. for
 , one can assume
, one can assume  and
and  to be plane waves of momentum
to be plane waves of momentum 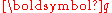 , which leads to the energy spectrum
, which leads to the energy spectrum
For large
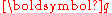 , the dispersion relation is quadratic in
, the dispersion relation is quadratic in 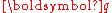 as one would expect for usual non interacting single particle excitations. For small
as one would expect for usual non interacting single particle excitations. For small  , the dispersion relation is linear
, the dispersion relation is linear
with
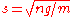 being the speed of sound in the condensate. The fact that
being the speed of sound in the condensate. The fact that  shows, according to Landau's criterion, that the condensate is a superfluid, meaning that if an object is moved in the condensate at a velocity inferior to s, it will not be energetically favorable to produce excitations and the object will move without dissipation, which is a characteristic of a superfluid
shows, according to Landau's criterion, that the condensate is a superfluid, meaning that if an object is moved in the condensate at a velocity inferior to s, it will not be energetically favorable to produce excitations and the object will move without dissipation, which is a characteristic of a superfluidSuperfluid
Superfluidity is a state of matter in which the matter behaves like a fluid without viscosity and with extremely high thermal conductivity. The substance, which appears to be a normal liquid, will flow without friction past any surface, which allows it to continue to circulate over obstructions and...
. Experiments have been done to prove this superfluidity of the condensate, using a tightly focused blue-detuned laser .
The same dispersion relation is found when the condensate is described from a microscopical approach using the formalism of second quantization.

