Graded poset - AbsoluteAstronomy.com

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, in the branch of combinatorics

Combinatorics

Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...

, a graded poset, sometimes called a ranked poset (but see the article

Ranked poset

In mathematics, a ranked partially ordered set - or poset - may be either:* a graded poset, or* a poset that has the property that for every element x, all maximal chains among those with x as greatest element have the same finite length, or...

for an alternative meaning), is a partially ordered set

Partially ordered set

In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...

(poset) P equipped with a rank function ρ from P to N compatible with the ordering (so ρ(x)<ρ(y) whenever x < y) such that whenever y covers

Covering relation

In mathematics, especially order theory, the covering relation of a partially ordered set is the binary relation which holds between comparable elements that are immediate neighbours...

x, then

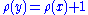. The value of the rank function for an element of the poset is called its rank.

Sometimes the term rank refers to a subset of all elements of the poset which have the same rank value. To avoid the confusion sometimes the term rank level is used for this purpose.

Graded posets play an important role in combinatorics

Combinatorics

and can be visualized by means of a Hasse diagram

Hasse diagram

In order theory, a branch of mathematics, a Hasse diagram is a type of mathematical diagram used to represent a finite partially ordered set, in the form of a drawing of its transitive reduction...

Examples

Some examples of graded posets (with in parentheses the rank function) are:

the natural numbers N, with their usual order (rank: the number itself), or some interval [0,N] of this poset,
Nⁿ, with the product order
Product order
In mathematics, given two ordered sets A and B, one can induce a partial ordering on the Cartesian product A × B. Giventwo pairs and in A × B, one sets ≤...

(sum of the coefficients), or a subposet of it that is a product of intervals,
the positive integers, ordered by divisibility (number of prime factors, counted with multiplicity), or a subposet of it formed by the divisors of a fixed N,
the Boolean lattice of finite subsets of a set (number of elements of the subset),
the lattice of partitions of a set into finitely many parts, ordered by reverse refinement (number of parts),
the lattice of partitions of a finite set X, ordered by refinement (number of elements of X minus number of parts),
a group and a generating set, or equivalently its Cayley graph
Cayley graph
In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...

, ordered by the weak or strong Bruhat order
Bruhat order
In mathematics, the Bruhat order is a partial order on the elements of a Coxeter group, that corresponds to the inclusion order on Schubert varieties.-History:The Bruhat order on the Schubert varieties of a flag manifold or Grassmannian...

, and ranked by word length (length of shortest reduced word).
- In particular for Coxeter group
  Coxeter group
  In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
  
  s, for example permutation
  Permutation
  In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
  
  s of a totally ordered n-element set, with either the weak or strong Bruhat order
  Bruhat order
  In mathematics, the Bruhat order is a partial order on the elements of a Coxeter group, that corresponds to the inclusion order on Schubert varieties.-History:The Bruhat order on the Schubert varieties of a flag manifold or Grassmannian...
  
  (number of adjacent inversions),
geometric lattices, such as the lattice of subspaces of a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...

(dimension of the subspace),
the distributive lattice
Distributive lattice
In mathematics, distributive lattices are lattices for which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection...

of finite lower sets of another poset (number of elements),
Young's lattice
Young's lattice
In mathematics, Young's lattice is a partially ordered set and a lattice that is formed by all integer partitions. It is named after Alfred Young, who in a series of papers On quantitative substitutional analysis developed representation theory of the symmetric group...

, a particular instance of the previous example (number of boxes in the Young diagram),
face lattices of convex polytope
Convex polytope
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...

s (dimension of the face, plus one),
abstract polytope
Abstract polytope
In mathematics, an abstract polytope, informally speaking, is a structure which considers only the combinatorial properties of a traditional polytope, ignoring many of its other properties, such as angles, edge lengths, etc...

s ("distance" from the least face, minus one ),
abstract simplicial complex
Abstract simplicial complex
In mathematics, an abstract simplicial complex is a purely combinatorial description of the geometric notion of a simplicial complex, consisting of a family of finite sets closed under the operation of taking subsets...

es (number of elements of the simplex).

Alternative characterizations

A bounded poset admits a grading if and only if all maximal chains in P have the same length: setting the rank of the least element to 0 then determines the rank function completely. This covers many finite cases of interest. However, unbounded posets can be more complicated.

A candidate rank function, compatible with the ordering, makes a poset into graded poset if and only if, whenever one has x < z with z of rank n+1, an element y of rank n can be found with x ≤ y < z. This condition is sufficient because if z is taken to be a cover of x, the only possible choice is y = x showing that the ranks of x and z differ by 1, and it is necessary because in a graded poset one can take for y any element of maximal rank with x ≤ y < z, which always exists and is covered by z.

Often a poset comes with a natural candidate for a rank function; for instance if its elements are finite subsets of some base set B, one can take the number of elements of those subsets. Then the criterion just given can be more practical than the definition because it avoids mention of covers. For instance if B is itself a poset, and P consists of its finite lower sets (subsets for which with every one of its elements, all smaller elements are also in the subset), then the criterion is automatically satisfied, since for lower sets x ⊂ z there is always a maximal element

Maximal element

In mathematics, especially in order theory, a maximal element of a subset S of some partially ordered set is an element of S that is not smaller than any other element in S. The term minimal element is defined dually...

of z that is absent from x, and it can be removed from z to form y.

In some common posets such as the face lattice of a convex polytope

Convex polytope

A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...

there is a natural grading by dimension

Dimension

In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...

, which if used as rank function would give the minimal element, the empty face, rank –1. In such cases it might be convenient to bend the definition stated above by adjoining the value –1 to the set of values allowed for the rank function. Allowing arbitrary integers as rank would however give a fundamentally different notion; for instance the existence of a minimal element would no longer be assured.

A graded poset cannot have any elements x for which arbitrarily long chains with greatest element x exist, as otherwise it would have to have elements of arbitrarily small (and eventually negative) rank. For instance, the integer

Integer

The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...

s (with the usual order) cannot be a graded poset, nor can any interval (with more than one element) of rational or real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s. (In particular, graded posets are well-founded, meaning that they satisfy the descending chain condition (DCC): they do not contain any infinite descending chain

Infinite descending chain

Given a set S with a partial order ≤, an infinite descending chain is a chain V that is a subset of S upon which ≤ defines a total order such that V has no least element, that is, an element m such that for all elements n in V it holds that m ≤ n.As an example, in the set of integers, the chain...

s.) Henceforth we shall therefore only consider posets in which this does not happen. This implies that whenever x < y we can get from x to y by repeatedly choosing a cover, finitely many times. It also means that compatibility of ρ with the ordering follows from the requirement about covers.

Note that graded posets need not satisfy the ascending chain condition

Ascending chain condition

The ascending chain condition and descending chain condition are finiteness properties satisfied by some algebraic structures, most importantly, ideals in certain commutative rings...

(ACC): for instance, the natural numbers contain the infinite ascending chain

.

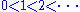A poset is graded if and only if every connected component of its comparability graph

Comparability graph

In graph theory, a comparability graph is an undirected graph that connects pairs of elements that are comparable to each other in a partial order...

is graded, so further characterizations will suppose this comparability graph to be connected. On each connected component the rank function is only unique up to a uniform shift (so the rank function can always be chosen so that the elements of minimal rank in their connected component have rank 0).

If P has a least element Ô then being graded is equivalent to the condition that for any element x all maximal chains in the interval [Ô,x] have the same length. This condition is necessary since every step in a maximal chain is a covering relation, which should change the rank by 1. The condition is also sufficient, since when it holds, one can use the mentioned length to define the rank of x (the length of a finite chain is its number of "steps", so one less than its number of elements), and whenever x covers y, adjoining x to a maximal chain in [Ô,y] gives a maximal chain in [Ô,x].

If P also has a greatest element

Greatest element

In mathematics, especially in order theory, the greatest element of a subset S of a partially ordered set is an element of S which is greater than or equal to any other element of S. The term least element is defined dually...

Î (so that it is a bounded poset), then the previous condition can be simplified to the requirement that all maximal chains in P have the same (finite) length. This suffices, since any pair of maximal chains in [Ô,x] can be extended by a maximal chain in [x,Î] to give a pair of maximal chains in P.

Note Stanley

Richard P. Stanley

Richard Peter Stanley is the Norman Levinson Professor of Applied Mathematics at the Massachusetts Institute of Technology, in Cambridge, Massachusetts. He received his Ph.D. at Harvard University in 1971 under the supervision of Gian-Carlo Rota...

defines a poset to be graded of length n if all its maximal chains have length n (Stanley 1997, p.99). This definition is given in a context where interest is mostly in finite posets, and although the book subsequently often drops the part "of length n", it does not seem appropriate to use this as definition of "graded" for general posets, because (1) it says nothing about posets whose maximal chains are infinite, in particular (2) it excludes important posets like Young's lattice

Young's lattice

In mathematics, Young's lattice is a partially ordered set and a lattice that is formed by all integer partitions. It is named after Alfred Young, who in a series of papers On quantitative substitutional analysis developed representation theory of the symmetric group...

. Also it is not clear why in a graded poset all minimal elements, as well as all maximal elements, should be required to have the same length, even if Stanley gives examples making clear that he does mean to require that (ibid, pp.216 and 219).

The usual case

Many authors in combinatorics

Combinatorics

define graded posets in such a way that all minimal elements of P must have rank 0, and moreover that there is a maximal rank r which is the rank of any maximal element. Then being graded means that all maximal chains have length r, as is indicated above. In this case one says that P has rank r.

Furthermore, in this case with the rank levels are associated the rank numbers or Whitney numbers . These number

Number

A number is a mathematical object used to count and measure. In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers....

s are defined by 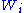= number of elements of P having rank i .

The Whitney numbers are connected with a lot of important combinatorial theorem

Theorem

In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...

s. The classic example is Sperner's theorem which can be formulated as follows:

For the powerset 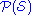of every finite set 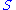the maximum cardinality of a Sperner family
Sperner family
In combinatorics, a Sperner family , named in honor of Emanuel Sperner, is a set system in which no element is contained in another. Formally,...

equals the maximum Whitney number.

This means:

Every finite
Finite
Finite is the opposite of infinite. It may refer to:*Finite set, having a number of elements given by some natural number*Finite verb, being inflected for person and for tense...

powerset has the Sperner property
Sperner property of a partially ordered set
In the order-theoretic mathematics, a graded partially ordered set is said to have the Sperner property , if no antichain within it is larger than the largest rank level in the poset.Since every rank level is itself an antichain, the Sperner property is equivalently the property that some rank...

Examples

Alternative characterizations

The usual case

See also