Giuga number
Encyclopedia
A Giuga number is a composite number
n such that for each of its distinct prime factor
s pi we have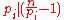
, or equivalently such that for each of its distinct prime factor
s pi we have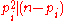
.
Another test for a Giuga number due to Takashi Agoh is: a composite number
n is a Giuga number if and only if
the congruence
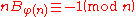
holds true, where B is a Bernoulli number
and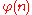
is Euler's totient function
.
An equivalent formulation due to Giuseppe Giuga is: a composite number
n is a Giuga number if and only if the congruence
and if and only if
The Giuga numbers are named after the mathematician Giuseppe Giuga, and relate to his conjecture on primality.
The sequence of Giuga numbers begins
For example, 30 is a Giuga number since its prime factors are 2, 3 and 5, and we can verify that
The prime factors of a Giuga number must be distinct. If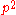
divides 
, then it follows that 
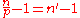, where 
is divisible by 
. Hence, 
would not be divisible by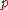 
, and thus 
would not be a Giuga number.
Thus, only square-free integer
s can be Giuga numbers. For example, the factors of 60 are 2, 2, 3 and 5, and 60/2 - 1 = 29, which is not divisible by 2. Thus, 60 is not a Giuga number.
This rules out squares of primes, but semiprime
s cannot be Giuga numbers either. For if
, with 
primes, then
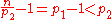, so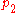 
will not divide 
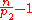, and thus 
is not a Giuga number.
All known Giuga numbers are even. If an odd Giuga number exists, it must be the product of at least 14 prime
s. It is not known if there are infinitely many Giuga numbers.
It has been conjectured by Paolo P. Lava (2009) that Giuga numbers are the solutions of the differential equation n'=n+1, being n' the arithmetic derivative
of n.
Composite number
A composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....
n such that for each of its distinct prime factor
Prime factor
In number theory, the prime factors of a positive integer are the prime numbers that divide that integer exactly, without leaving a remainder. The process of finding these numbers is called integer factorization, or prime factorization. A prime factor can be visualized by understanding Euclid's...
s pi we have
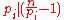, or equivalently such that for each of its distinct prime factorPrime factor
In number theory, the prime factors of a positive integer are the prime numbers that divide that integer exactly, without leaving a remainder. The process of finding these numbers is called integer factorization, or prime factorization. A prime factor can be visualized by understanding Euclid's...
s pi we have
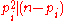.Another test for a Giuga number due to Takashi Agoh is: a composite number
Composite number
A composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....
n is a Giuga number if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the congruence
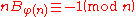
holds true, where B is a Bernoulli number
Bernoulli number
In mathematics, the Bernoulli numbers Bn are a sequence of rational numbers with deep connections to number theory. They are closely related to the values of the Riemann zeta function at negative integers....
and
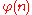is Euler's totient functionEuler's totient function
In number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
.
An equivalent formulation due to Giuseppe Giuga is: a composite number
Composite number
A composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....
n is a Giuga number if and only if the congruence
and if and only if
The Giuga numbers are named after the mathematician Giuseppe Giuga, and relate to his conjecture on primality.
The sequence of Giuga numbers begins
- 30, 858, 1722, 66198, 2214408306, … .
For example, 30 is a Giuga number since its prime factors are 2, 3 and 5, and we can verify that
- 30/2 - 1 = 14, which is divisible by 2,
- 30/3 - 1 = 9, which is 3 squared, and
- 30/5 - 1 = 5, the third prime factor itself.
The prime factors of a Giuga number must be distinct. If
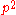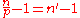divides , then it follows that , where is divisible by . Hence, would not be divisible by 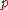, and thus would not be a Giuga number.Thus, only square-free integer
Square-free integer
In mathematics, a square-free, or quadratfrei, integer is one divisible by no perfect square, except 1. For example, 10 is square-free but 18 is not, as it is divisible by 9 = 32...
s can be Giuga numbers. For example, the factors of 60 are 2, 2, 3 and 5, and 60/2 - 1 = 29, which is not divisible by 2. Thus, 60 is not a Giuga number.
This rules out squares of primes, but semiprime
Semiprime
In mathematics, a semiprime is a natural number that is the product of two prime numbers. The first few semiprimes are 4, 6, 9, 10, 14, 15, 21, 22, 25, 26, ... ....
s cannot be Giuga numbers either. For if
, with primes, then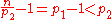, so 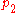will not divide 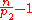, and thus is not a Giuga number.All known Giuga numbers are even. If an odd Giuga number exists, it must be the product of at least 14 prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s. It is not known if there are infinitely many Giuga numbers.
It has been conjectured by Paolo P. Lava (2009) that Giuga numbers are the solutions of the differential equation n'=n+1, being n' the arithmetic derivative
Arithmetic derivative
In number theory, the arithmetic derivative, or number derivative, is a function defined for integers, based on prime factorization, by analogy with the product rule for the derivative of a function that is used in mathematical analysis.-Definition:...
of n.