Arithmetic derivative
Encyclopedia
In number theory
, the arithmetic derivative, or number derivative, is a function defined for integer
s, based on prime factorization, by analogy with the product rule
for the derivative of a function
that is used in mathematical analysis
.
To coincide with the Leibniz rule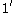
is defined to be 
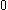, as is 
. Explicitly, assume that
where
are distinct primes and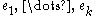 
are positive integers. Then
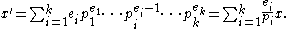
The arithmetic derivative also preserves the power rule (for primes):
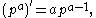
where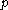
is prime and 
is a positive integer. For example,
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the arithmetic derivative, or number derivative, is a function defined for integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, based on prime factorization, by analogy with the product rule
Product rule
In calculus, the product rule is a formula used to find the derivatives of products of two or more functions. It may be stated thus:'=f'\cdot g+f\cdot g' \,\! or in the Leibniz notation thus:...
for the derivative of a function
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
that is used in mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
.
Definition
For natural numbers defined as follows:-
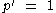for any prime 
. -
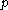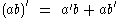for any 
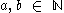(Leibniz ruleProduct ruleIn calculus, the product rule is a formula used to find the derivatives of products of two or more functions. It may be stated thus:'=f'\cdot g+f\cdot g' \,\! or in the Leibniz notation thus:...
).
To coincide with the Leibniz rule
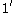is defined to be , as is . Explicitly, assume thatwhere
are distinct primes and 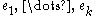are positive integers. Then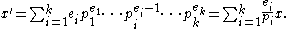The arithmetic derivative also preserves the power rule (for primes):
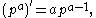
where
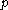is prime and is a positive integer. For example,-
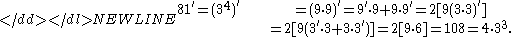
The sequence of number derivatives for k = 0, 1, 2, ... begins :
- 0, 0, 1, 1, 4, 1, 5, 1, 12, 6, 7, 1, 16, 1, 9, ....
E. J. Barbeau was the first to formalize this definition. He extended it to all integers by proving that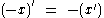
uniquely defines the derivative over the integers. Barbeau also further extended it to rational numbers. Victor Ufnarovski and Bo Åhlander expanded it to certain irrationals. In these extensions, the formula above still applies, but the exponents 
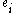are allowed to be arbitrary rational numbers.
Inequalities and bounds
E. J. Barbeau examined bounds of the arithmetic derivative. He found that the arithmetic derivative of natural numbers is bounded by-
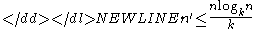
where k is the least prime in n and
-
where s is the number of prime factors in n.
In both bounds above, equality occurs only if n is a perfect power of 2, that is
for some m.
Alexander Loiko, Jonas Olsson and Niklas Dahl found that it is impossible to find similar bounds for the arithmetic derivative extended to rational numbers by proving that between any two rational numbers there are other rationals with arbitrary large or small derivatives.
Relevance to number theory
Victor Ufnarovski and Bo Åhlander have detailed the function's connection to famous number-theoretic conjectures like the twin prime conjecture, the prime triples conjecture, and Goldbach's conjectureGoldbach's conjectureGoldbach's conjecture is one of the oldest unsolved problems in number theory and in all of mathematics. It states:A Goldbach number is a number that can be expressed as the sum of two odd primes...
. For example, Goldbach's conjecture would imply, for each k > 1 the existence of an n so that n' = 2k. The twin prime conjecture would imply that there are infinitely many k for which k= 1.
-