Gibbons-Hawking-York boundary term
Encyclopedia
In general relativity
, the Gibbons–Hawking–York boundary term is a term that needs to be added to the Einstein-Hilbert action
when the underlying spacetime
manifold
has a boundary.
The Einstein-Hilbert action is the basis for the most elementary variational principle
from which the field equations of general relativity
can be defined. However, the use of the Einstein-Hilbert action is appropriate only when the underlying spacetime manifold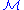
is closed
, i.e., a manifold which is both compact and without boundary. In the event that the manifold has a boundary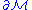
, the action should be supplemented by a boundary term so that the variational principle is well-defined.
The necessity of such a boundary term was first realised by York
and later refined in a minor way by Gibbons
and Hawking
.
For a manifold that isn't closed, the appropriate action is
,
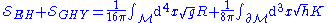where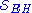
is the Einstein-Hilbert action, 
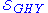is the Gibbons–Hawking–York boundary term, 
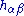is the induced metric
on the boundary and
is the trace of the second fundamental form. Varying the action with respect to the metric 
gives the Einstein equations
; the addition of the boundary term means that in performing the variation, the geometry of the boundary encoded in the induced metric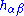
is fixed. There remains ambiguity in the action up to an arbitrary functional of the induced metric 
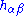. The equations of motion constrain the extrinsic curvature to be zero.
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, the Gibbons–Hawking–York boundary term is a term that needs to be added to the Einstein-Hilbert action
Einstein-Hilbert action
The Einstein–Hilbert action in general relativity is the action that yields the Einstein's field equations through the principle of least action...
when the underlying spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
has a boundary.
The Einstein-Hilbert action is the basis for the most elementary variational principle
Variational principle
A variational principle is a scientific principle used within the calculus of variations, which develops general methods for finding functions which minimize or maximize the value of quantities that depend upon those functions...
from which the field equations of general relativity
Einstein field equations
The Einstein field equations or Einstein's equations are a set of ten equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy...
can be defined. However, the use of the Einstein-Hilbert action is appropriate only when the underlying spacetime manifold
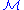is closedClosed manifold
In mathematics, a closed manifold is a type of topological space, namely a compact manifold without boundary. In contexts where no boundary is possible, any compact manifold is a closed manifold....
, i.e., a manifold which is both compact and without boundary. In the event that the manifold has a boundary
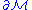, the action should be supplemented by a boundary term so that the variational principle is well-defined.The necessity of such a boundary term was first realised by York
James W. York
James W. York, Jr. is an American mathematical physicist who is well known for his many important contributions to the theory of general relativity...
and later refined in a minor way by Gibbons
Gary Gibbons
Gary William Gibbons , FRS, is a British theoretical physicist. Gibbons studied in Cambridge,where in 1969 he became a research student under the supervision of Dennis Sciama. When Sciama moved to Oxford, he became a student of Stephen Hawking, obtaining his PhD from Cambridge in 1973...
and Hawking
Stephen Hawking
Stephen William Hawking, CH, CBE, FRS, FRSA is an English theoretical physicist and cosmologist, whose scientific books and public appearances have made him an academic celebrity...
.
For a manifold that isn't closed, the appropriate action is
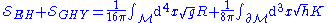,where
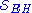is the Einstein-Hilbert action, 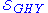is the Gibbons–Hawking–York boundary term, 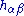is the induced metricInduced metric
In mathematics and theoretical physics, the induced metric is the metric tensor defined on a submanifold which is calculated from the metric tensor on a larger manifold into which the submanifold is embedded...
on the boundary and
is the trace of the second fundamental form. Varying the action with respect to the metric gives the Einstein equationsEinstein field equations
The Einstein field equations or Einstein's equations are a set of ten equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy...
; the addition of the boundary term means that in performing the variation, the geometry of the boundary encoded in the induced metric
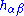is fixed. There remains ambiguity in the action up to an arbitrary functional of the induced metric 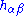. The equations of motion constrain the extrinsic curvature to be zero.