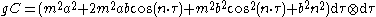Induced metric
Encyclopedia
In mathematics
and theoretical physics
, the induced metric is the metric tensor
defined on a submanifold
which is calculated from the metric tensor on a larger manifold
into which the submanifold is embedded. It may be calculated using the following formula:
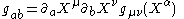
Here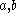
describe the indices of coordinates 
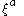of the submanifold while the functions 
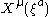encode the embedding into the higher-dimensional manifold whose tangent indices are denoted 
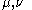. Note: Einstein summation convention was used.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and theoretical physics
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, the induced metric is the metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
defined on a submanifold
Submanifold
In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
which is calculated from the metric tensor on a larger manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
into which the submanifold is embedded. It may be calculated using the following formula:
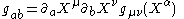
Here
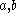describe the indices of coordinates 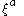of the submanifold while the functions 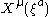encode the embedding into the higher-dimensional manifold whose tangent indices are denoted 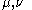. Note: Einstein summation convention was used.Example - Curve on a torus
Let-
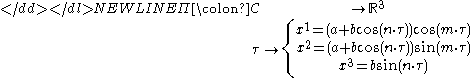
be a map from the domain of the curve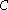
with parameter 
into the euclidean manifold 
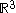. Here 
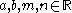are constants.
Then there is a metric given on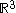
as
.
and we compute
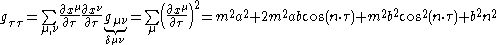
Therefore